primordial: inflationary equation solver

primordial:	inflationary equation solver
Author:	Will Handley
Version:	0.0.14
Homepage:	https://github.com/williamjameshandley/primordial
Documentation:	http://primordial.readthedocs.io/

Description

primordial is a python package for solving cosmological inflationary equations.

It is very much in beta stage, and currently being built for research purposes.

Example Usage

Plot Background evolution

import numpy
import matplotlib.pyplot as plt
from primordial.solver import solve
from primordial.equations.inflation_potentials import ChaoticPotential
from primordial.equations.t.inflation import Equations, KD_initial_conditions
from primordial.equations.events import Inflation, Collapse

fig, ax = plt.subplots(3,sharex=True)
for K in [-1, 0, +1]:
     m = 1
     V = ChaoticPotential(m)
     equations = Equations(K, V)

     events= [Inflation(equations),                    # Record inflation entry and exit
              Inflation(equations, -1, terminal=True), # Stop on inflation exit
              Collapse(equations, terminal=True)]      # Stop if universe stops expanding

     N_p = -1.5
     phi_p = 23
     t_p = 1e-5
     ic = KD_initial_conditions(t_p, N_p, phi_p)
     t = numpy.logspace(-5,10,1e6)

     sol = solve(equations, ic, t_eval=t, events=events)

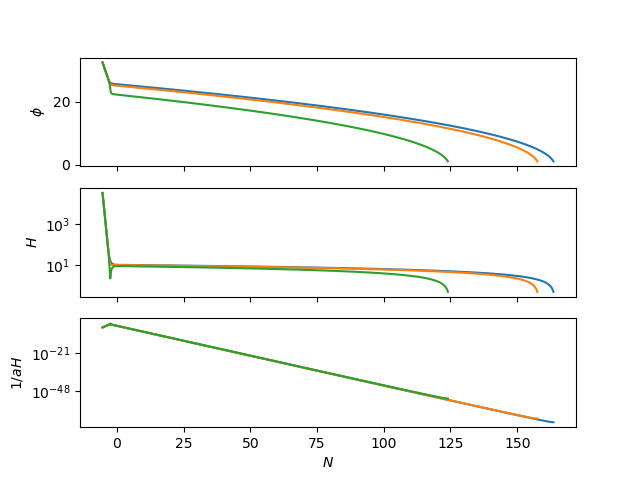
     ax[0].plot(sol.N(t),sol.phi(t))
     ax[0].set_ylabel(r'$\phi$')

     ax[1].plot(sol.N(t),sol.H(t))
     ax[1].set_yscale('log')
     ax[1].set_ylabel(r'$H$')

     ax[2].plot(sol.N(t),1/(sol.H(t)*numpy.exp(sol.N(t))))
     ax[2].set_yscale('log')
     ax[2].set_ylabel(r'$1/aH$')

ax[-1].set_xlabel('$N$')

Plot mode function evolution

import numpy
import matplotlib.pyplot as plt
from primordial.solver import solve
from primordial.equations.inflation_potentials import ChaoticPotential
from primordial.equations.t.mukhanov_sasaki import Equations, KD_initial_conditions
from primordial.equations.events import Inflation, Collapse, ModeExit

fig, axes = plt.subplots(3,sharex=True)
for ax, K in zip(axes, [-1, 0, +1]):
    ax2 = ax.twinx()
    m = 1
    V = ChaoticPotential(m)
    k = 100
    equations = Equations(K, V, k)

    events= [
            Inflation(equations),                    # Record inflation entry and exit
            Collapse(equations, terminal=True),      # Stop if universe stops expanding
            ModeExit(equations, +1, terminal=True, value=1e1*k)   # Stop on mode exit
            ]


    N_p = -1.5
    phi_p = 23
    t_p = 1e-5
    ic = KD_initial_conditions(t_p, N_p, phi_p)
    t = numpy.logspace(-5,10,1e6)

    sol = solve(equations, ic, t_eval=t, events=events)

    N = sol.N(t)
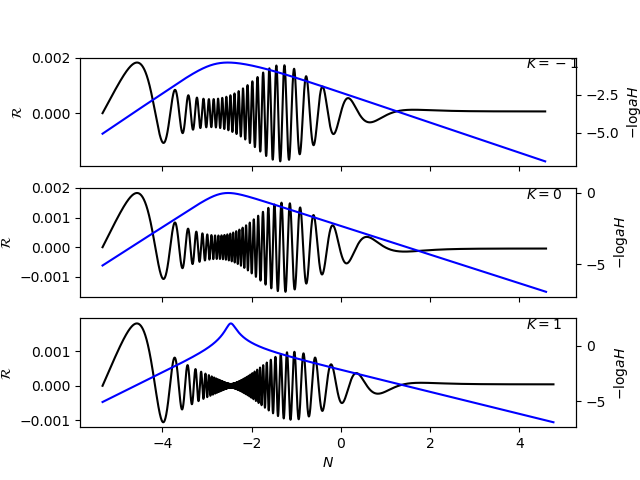
    ax.plot(N,sol.R1(t), 'k-')
    ax2.plot(N,-numpy.log(sol.H(t))-N, 'b-')

    ax.set_ylabel('$\mathcal{R}$')
    ax2.set_ylabel('$-\log aH$')

    ax.text(0.9, 0.9, r'$K=%i$' % K, transform=ax.transAxes)

axes[-1].set_xlabel('$N$')

To do list

Eventually would like to submit this to JOSS. Here are things to do before then:

Cosmology

Slow roll initial conditions
add \eta as independent variable
add \phi as independent variable

Code

Documentation
Tests
- 100% coverage
- interpolation

williamjameshandley/primordial