Data Structures and Algorithms

Why do we learn data-structures?

Software from an abstract level consists of sets of data structure interacting with each other. Almost everything you will deal with in software engineering is realated to data structures in one way or another. When constructing algorithms to solve problems, the data structures you decide to use will represent the information flow in your algorithm. The data structure will determine how you're able to access the data, sort it, add to it, remove from it, etc.

Big O Resource - Big O Cheat Sheet

Data Structures Part I (Abstract Data Types)

They pertain to linear data structures.

Stack

A last-in-first-out (LIFO) data structure. Works similarly to a stack of dirty plates waiting to be washed. The plates added last to the stack will be washed first.

We can implement a stack with the following properties:

push(value) - adds a value to the top of the stack
pop(value) - takes a value from the top of the stack
peak() - Looks at the object at the top of this stack without removing it from the stack

Video on stacks

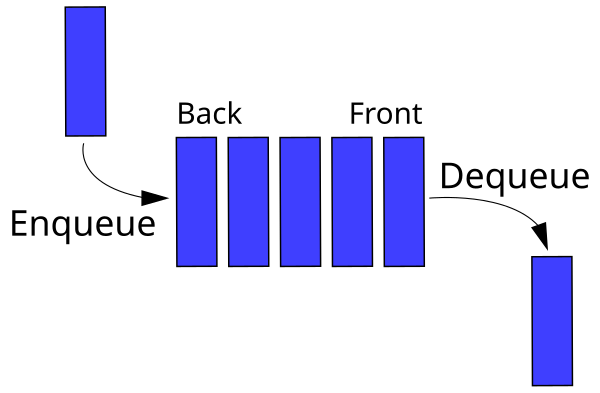
Queue

A first-in-first-out (FIFO) data structure. Works similarly to a line of people at a bustop or a supermarket waiting to check items out.

Implement a queue with the following properties:

enqueue(value) - adds a value to the end of the queue
dequeue(value) - takes a value from the front of the queue and returns that value
size() - returns the number of items in the queue
isEmpty() - returns a boolean based on weathere or not the queue is empty

Extra resource on Queues Video on queues

Linked-List

A group of nodes which together represent a sequence. Each node is composed of a data and a reference(link), to the next node in the sequence.

Implement a Linked-List with the following properties:

head - property indicating the first value in the linked-list
tail - property indicating the last value in the linked-list
addtoTail(value) - method which takes a value and adds it the end of the list
removeHead() - method which removes the first node in the list and returns it's value
contains(value) - method which takes a value and return a boolean depending on whether or not the value is in the list.

Things to think about:

What is the time complexity of the above functions?
How do you know that you have reached the end of a linked-list (What does the next-pointer point to)?
How would you know that you have an empty linked list?

More on Linked Lists -linked lists are ordered sets of data items. -Each element contains a link to its successor -the last element of the sequence points to a null element -the data elements are called nodes

###inserting an element into the linked list

-create a new node for it -connect the next reference of the new node to the existing head node -then make the head of the linked list point to the new head node -if we pointed to the new node first we would lose access to all the existing elements in the linked list since there is no reference from the new head node to the previous head node

Video on single linked-lists

Data Structures Part II

Trees

A tree is a collection of nodes where each node consists of a value as well as a list of references to its children. Each node doesn't have a reference to its parent, just to their children. Meaning that each of the children are also individual trees.

Implement a Tree:

Has a children property: a collection of all the children.
has a addChild(value) method which take a value and adds it as a child of that tree.
Has a contains(value) method which take a value and searches the entire tree for that value. Returns a boolean.

Things to consider:

What is the time complexity of the above functions?
What are type of data structures are the children of trees?

Video on trees

Binary Search Trees

Binary search trees keep their values stored in a sorted fashion. When you traverse a binary search tree, you make the decision whether to go left or right based on comparison. Values less then the current leaf are stored to the left, while values larger than the current leaf are stored to the right. On average, each comparison allows you to skip over half of the tree, ensuring that lookup, deletion, and insertion can be done in logarthmic time.

Implement a binary search tree:

Has a left and right property which references the children on the left and right side
Has an insert(value) method which takes a value and places it in the correct position of the binary search tree
Has a contains(target) method which searches the entire binary search tree for a particular method

Video on binary search

willieaugustine/ms-7-dsa