MATLAB's function robustfit() enables to fit a polynomial to data whose residuals are not normally distributed, which is the implicit assumption of least squares (LSQ) methods. Non-normal residuals result, for example, from outliers in empirical data or noise which is not normally distributed. The function utilizes the Iteratively Reweighted Least Squares (IRLS) approach with data-adaptive weights.
The downside is that robustfit() does not support non-linear least squares problems which often arise if the mathematical model is non-linear in its parameters. The function lsqcurvefit() and lsqnonlin() provide means to solve non-linear LSQ with optional parameter bounds (due to the trust-region-reflective algorithm) but don't support weighted LSQ for robust estimation in the presence of outliers.
This MATLAB function is intended to give the best of both worlds, i.e. combine methods of robustfit() and lsqnonlin() to accomplish robust non-linear least squares calculations.
This function is tested in MATLAB R2016b but should scale to any modern MATLAB release.
The function depends on the following toolboxes:
- Statistics and Machine Learning Toolbox
- Optimization Toolbox
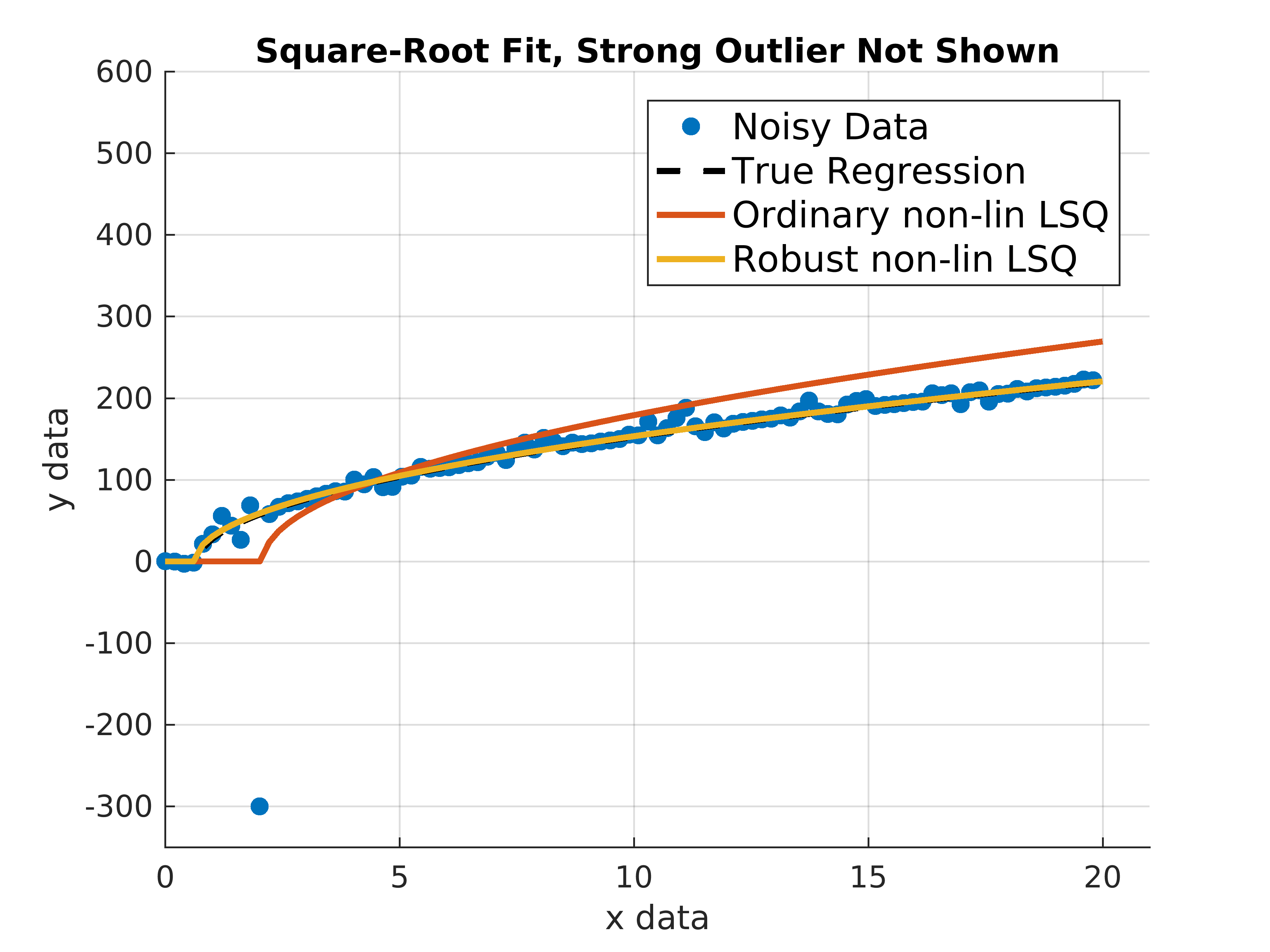
Consider the following problem. We want to fit a function to data which stems from a square-root function with a scale and location parameter. The data is noisy and exhibits strong outliers. Let's see how ordinary and robust non-linear least squares perform in this situation. The example is taken from the provided demo file.
% the model's true parameters
trueParams = [50, -0.7];
% create some noisy data using a square root function with 2 parameters and nasty noise
x = linspace(0, 20, 100);
modelFun = @(param, x) param(1)*sqrt(max(0, x + param(2)));
noise = 10*sin(x).^2 .* randn(size(x));
y = modelFun(trueParams, x) + noise;
% introduce outliers
y(11) = -300;
y(end) = 2000;
%%%% Fit the model %%%%
% make sure the parameters are within the following range
lb = [1, -inf];
ub = [inf, 10];
% initial guess
x0 = [1, -1];
% don't show infos from lsqcurvefit()
options = optimset(@lsqcurvefit);
options.Display = 'off';
% estimate parameters using ordinary and robust LSQ
estParamsOrdinary = lsqcurvefit(modelFun, x0, x, y, lb, ub, options);
estParamsRobust = robustlsqcurvefit(modelFun, x0, x, y, lb, ub, [], options);
figure;
hold on;
scatter(x, y, 'filled');
plot(x, modelFun(trueParams, x), 'k--', 'linewidth', 2);
plot(x, modelFun(estParamsOrdinary, x), 'linewidth', 2');
plot(x, modelFun(estParamsRobust, x), 'linewidth', 2);
hold off;
grid on;
legend(...
{'Noisy Data', 'True Regression', 'Ordinary non-lin LSQ', 'Robust non-lin LSQ'}, ...
'fontsize', 12 ...
);The code is licensed under BSD 3-Clause license.