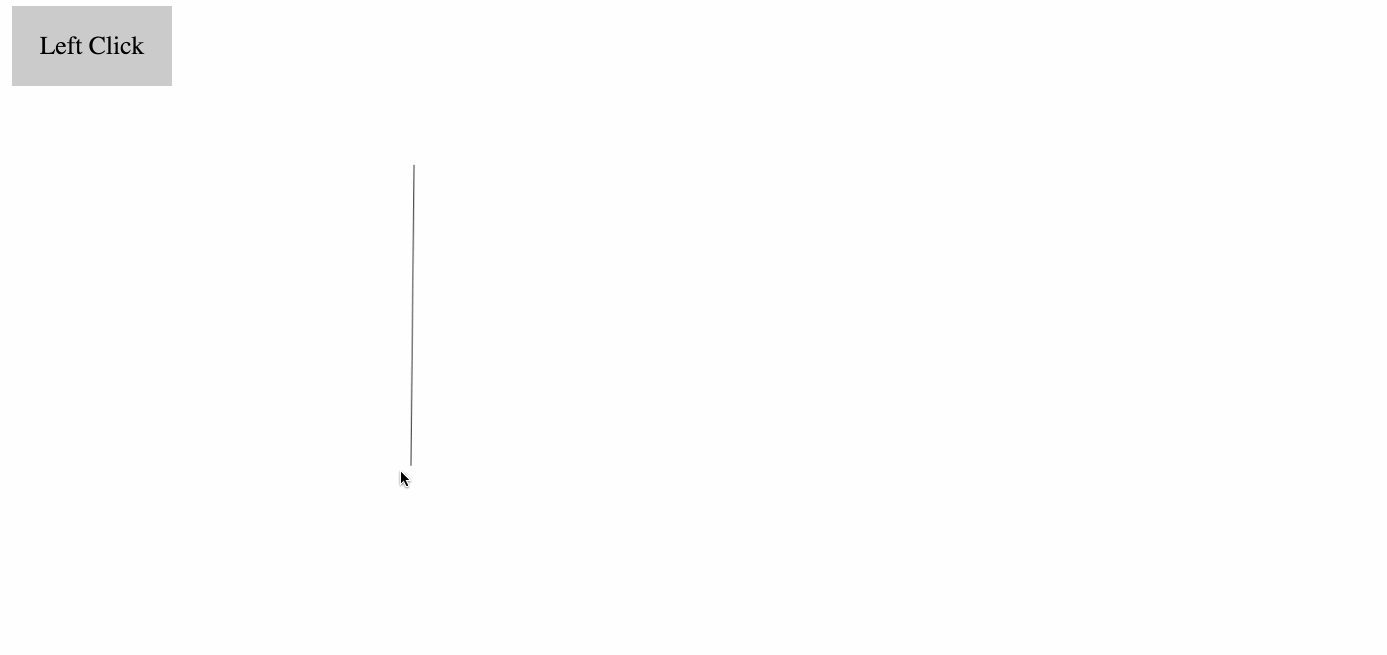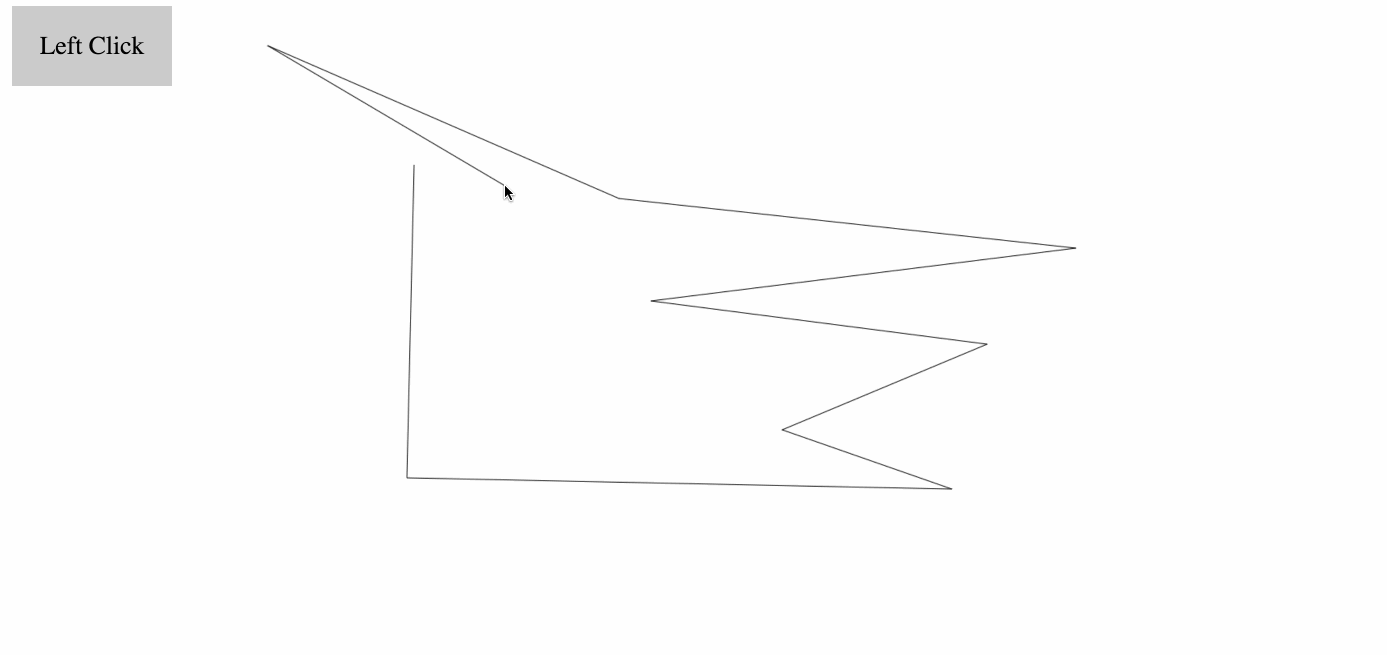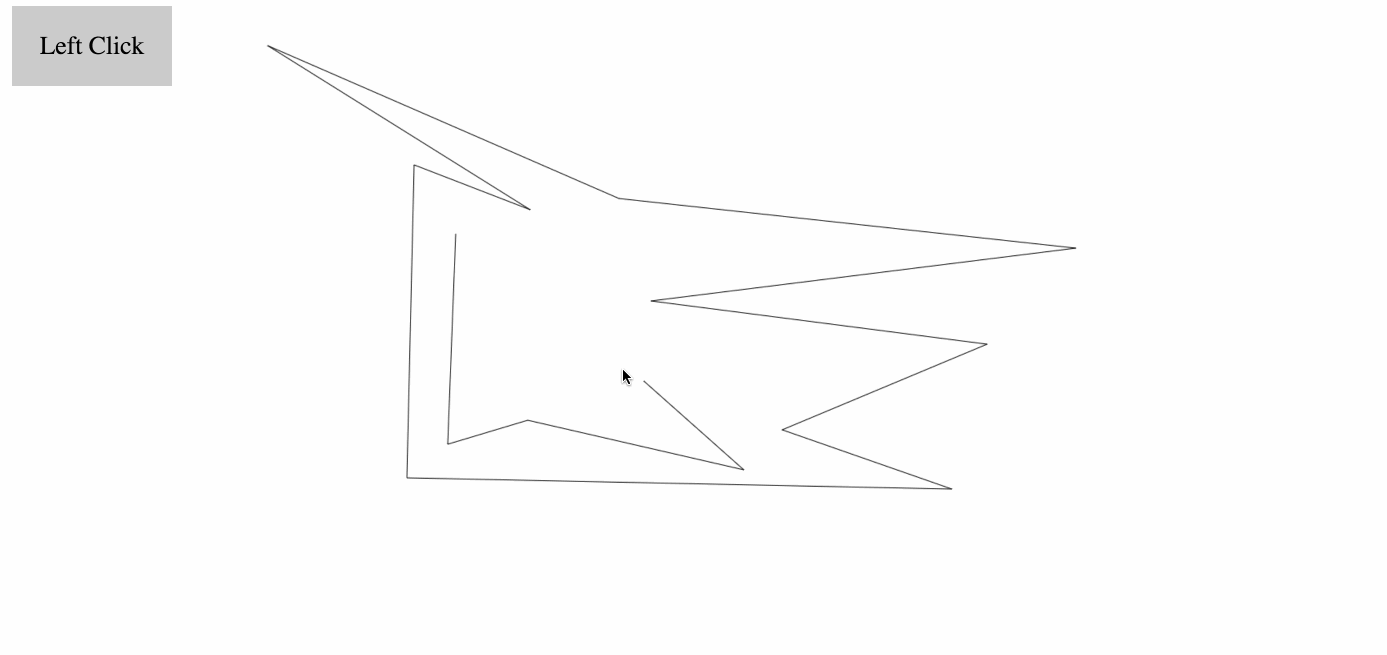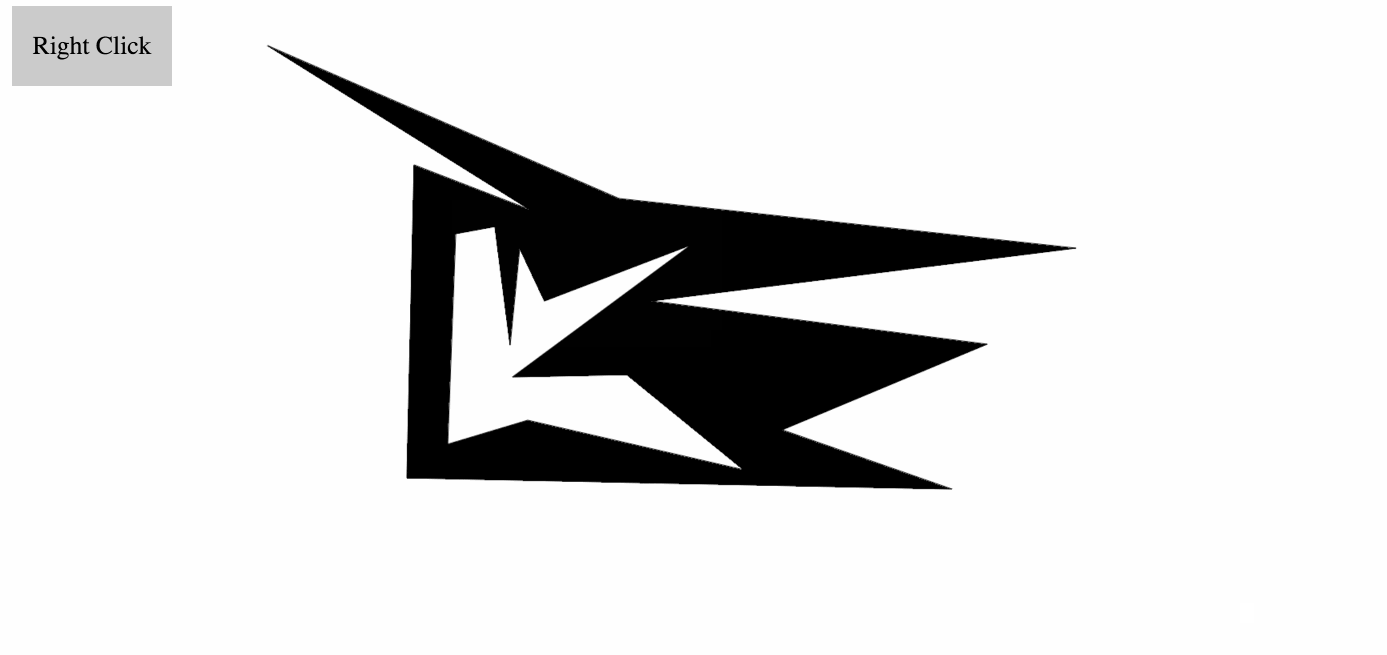任意多边形填充、裁剪、平移、旋转、缩放、翻转算法的实现。
# prepare
npm install -g yarn
yarn install
# develop
npm start
# build
npm run build左键添加点,右键闭合当前多边形。
进入界面后首先绘制外环,左键逆时针添加若干个外环点,右键闭合外环。
然后左键顺时针添加若干内环点,右键闭合内环(可以直接闭合,表示无内环)。
然后可以对多边形做各种操作:
- 平移:按 M,然后依次输入平移的 x、y 值
- 旋转:按 R,然后输入旋转的角度(°)
- 缩放:按 S,然后输入缩放系数
- 翻转:按 F,然后输入 x 或 y,代表翻转方向
- 填充:多边形完成后自动填充黑色,按 I 并依次输入 r、g、b (0-255)
- 裁剪:按 C,然后按照第一次输入多边形的方式输入裁剪多边形(暂时不支持内环,所以不需要内环的步骤),完成后自动裁剪。
算法使用 TypeScript 实现,使用 HTML5 Canvas API 在网页上作画,仅使用了 fillRect(x, y, 1, 1) 来模拟 setPixel(x, y)。在具体实现上,每个多边形仅记录了外环、内环的顶点和连接顺序,像素图是每次根据顶点计算而得到的。像素画布的尺寸就是真实的浏览器尺寸。
填充使用了边界标志填充法,实现了任意多边形(凹、凸、带内环)的填充,处理了所有边界情况,具体实现上,使用了一个标志矩阵来记录每个像素的边界情况,如果标志位是奇数,那么就需要翻转 inside,反之则不用。对于多边形的顶点,根据它跟相邻两个节点的关系,如果是一上一下,那么顶点像素位的标志加一,如果同上或者同下,标志位不变。对于边上的点,如果线段平行于 x 轴, 标志位不变,否则标志位加一。测试对于复杂的多边形,都能正确填充。
填充 demo:
裁剪使用 Weiler-Atherton 算法实现,并且利用计算几何边追赶的**,对 WA 算法做了一些改动,省略了预处理的过程。
由于算法的复杂性,实现中省略了内环的情况,仅能任意凹凸多边形被任意凹凸多边形裁剪,且对于一些边边、边点、点点重合的情况,以及可能切割出多个多边形的情况没有处理,仅保证实现了的部分的正确性。
算法的思路如下:
- 首先找到任何一个交点,如果找不到,判断两个多边形的包含关系直接得到结果,算法结束,否则记第一个节点为 P1。
- 使用两个指针分别代表两个多边形上的点,初始化全部指向 P1。定义点数组 intersections 代表结果,初始化为 [P1]。初始化 P 为 P1。
- 从 P 开始使用叉积判断当前两条边的相对关系。
- 靠外的边所属的多边形上的指针向前行走,边走边判断与另一个多边形的交点,直到遇到下一个交点,停止,记为 P2。
- 另一个多边形上的指针「追赶」上一个多边形的指针,将沿途经过的顶点加入 intersections,直到走到 P2。
- intersections 压入 P2,更新 P 为 P2。
- 如果 P 和 P1 相等,算法结束,返回 intersections,否则转 3。
简化后的算法和 WA 算法很相似,创新点:
- 不需要事先预处理得到所有交点并标记出入性。随着双指针行进的过程逐渐计算交点。
- 不需要区分出入点,从任何交点开始算法都是正确的。
裁剪 demo
因为只记录了每个多边形的顶点,可以简单地让每个顶点乘相应的变换矩阵完成变换,为了更好的界面效果,旋转、缩放操作是相对于重心的,翻转操作以重心所在的 x 轴或 y 轴为对称轴。