矩阵库

这是一个使用了C++标准库写出来的矩阵相关操作的库，能够完成矩阵求逆、转置、基本的算数运算。并且重载了大部分操作符，所以使用起来比较方便。

缺点是在矩阵乘法使用的是原生的算法，还没有优化，时间复杂度应该是O(n^3)。

主要的头文件在matrix目录下。

v1.3注意

v1.3为了完成部分功能，使用了C++17的特性。具体有：

if constexpr，在文件mat_type.h的函数Mat::Random中使用了这个特性。
在实现矩阵链式乘法的优化版本中，使用了std::variant来实现解析乘法优先级。

如果不支持C++14，可以选择Branch中的tag，找到指定的版本，返回v1.2.

v1.2需要C++14

已完成的功能

v1.3

算数运算
1. 基本类型
2. 加法
3. 减法、除法、(与常数的)乘法同样
4. 矩阵乘法
5. 转置和求逆
6. 随机数矩阵
7. 滤波章节例子3.1
8. 优化的链式乘法,编译器优化选项

使用方法和配置

在使用的cpp文件目录下，拷贝src目录下的所有hpp文件拷贝到你正在写的cpp文件同一级目录（或者某个地方你能够include）。或者自己创建复制其中内容都行。之后在使用的cpp文件同一级目录下#include "matrix.hpp"就可以了。

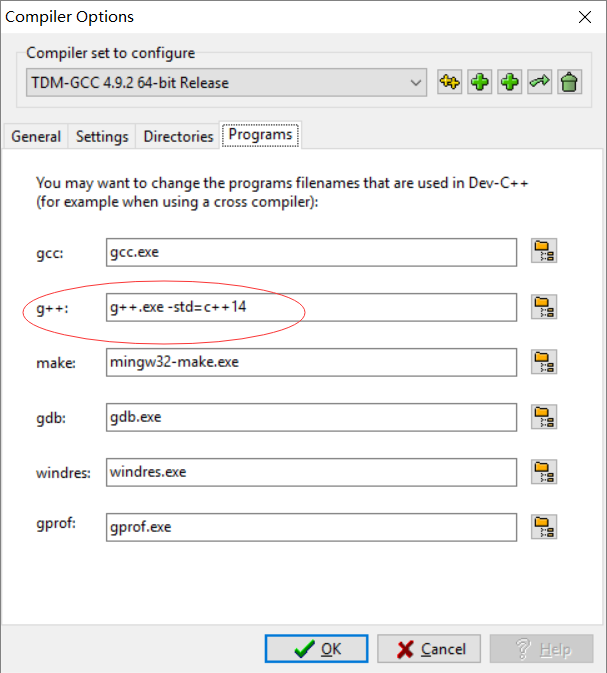
需要c++14。一般最新的dev-cpp都能够支持到c++14，17就不一定了。配置如图：

打开工具->编译选项
点击这个位子，program
在g++后面添加-std=c++14，注意与前面的g++.exe有个空格

1. 基本类型

矩阵的基础类型为wj::Mat<T>, T为double, float, int，分别对于类型Matd, Matf, Mati。

using Matd = wj::Mat<double>;
using Matf = wj::Mat<float>;
using Mati = wj::Mat<int>;

1.1构造函数和访问

// 一个3x3的矩阵
wj::Mati a{
           {1, 2, 3},
           {4, 5, 6},
           {7, 8, 9}};
// 一个3x4的矩阵，默认为元素全为0的矩阵
wj::Mat<int> b(3, 4);

// 构造之后可以通过以下两种方法访问/修改矩阵的每一个数
printf("我是a[0][0]:%i\n 我是a(1, 1):%i\n", matrix_3by3[0][0], matrix_3by3(1, 1));
/*
我是a[0][0]:1
我是a(1, 1):5
*/
a(1, 1) = 3;
a[1][1] = 3; // 同上

如果不想在每一个对象/函数前用wj::，可以在#include "matrix/matrix.h"之后使用using namespace wj;。（以下例子默认使用using...）

1.2 单位矩阵

// c 是一个3x3的单位矩阵
Matd c = Matd::Eye(3);

1.3 使用流进行(cout)输出

cout << a;
/* 输出：
matrix:
value_type: d
size:       3 x 3
[[1, 2, 3]
 [4, 5, 6]
 [7, 8, 9]]
 */

1.4 Clone()

Matd cl = a.Clone()

1.5 行列大小

std::size_t row = a.RowSize();
std::size_t col = a.ColSize();

2. 加法

如果矩阵之间的操作，行列不匹配则会抛出异常(invalid_argument)。

2.1 矩阵之间加法

Matd d = a + a;
/*
matrix:
value_type: d
size:       3 x 3
[[2, 4, 6]
 [8, 10, 12]
 [14, 16, 18]]
 */

2.2 矩阵和常数的加减法

Matd e = 2 + a;
// e = a + 2; 相同的结果
/*
matrix:
value_type: d
size:       3 x 3
[[3, 4, 5]
 [6, 7, 8]
 [9, 10, 11]]
 */

3. 减法、除法、(与常数的)乘法同样

4. 矩阵乘法

4.1 矩阵乘法

Matd f = c * a;
/*
matrix:
value_type: d
size:       3 x 3
[[1, 2, 3]
 [4, 5, 6]
 [7, 8, 9]]
 */

4.2 点乘

// a点乘d
Matd g = a.DotProduct(d);
/*
matrix:
value_type: d
size:       3 x 3
[[2, 8, 18]
 [32, 50, 72]
 [98, 128, 162]]
 */

5. 转置和求逆

转置和求逆，以及各种操作都是产生新的矩阵(Mat对象)。

Matd m{
       {1, 2, 0},
       {3, 4, 4},
       {5, 6, 3}};

cout << m.Transpose();
/*
matrix:
value_type: d
size:       3 x 3
[[1, 3, 5]
 [2, 4, 6]
 [0, 4, 3]]
*/

cout << m.Inverse();
/*
matrix:
value_type: d
size:       3 x 3
[[-1.2, -0.6, 0.8]
 [1.1, 0.3, -0.4]
 [-0.2, 0.4, -0.2]]
 */

6. 随机数矩阵

随机数矩阵使用Mat<T>的静态函数Mat<T>::Random(low, high, row, col)来生成。是随机数均匀分布，生成的类型是T。

例子：

Matd m = wj::Matd::Random(-100., 100., 5, 5);
cout << m;
/*
matrix:
value_type: d
size:       5 x 5
[[-73.6924, -8.26997, -56.2082, 35.7729, 86.9386]
 [3.88327, -93.0856, 5.94004, -98.4604, -86.6316]
 [37.3545, 86.0873, 5.38576, 30.7838, 40.2381]
 [52.4396, -90.5071, -34.3532, 51.2821, -26.9323]
 [96.5101, 50.6712, -85.4628, 76.9414, -12.7177]]
 */

Mati mm = wj::Mat<int>::Random(-100., 100., 5, 5);
cout << mm;
/*
matrix:
value_type: i
size:       5 x 5
[[-100, -74, 51, -8, 7]
 [-56, -91, 36, 36, 87]
 [-23, 4, 67, -94, -90]
 [6, 34, -99, -23, -87]
 [-17, 38, 18, 87, 70]]
 */

7. 滤波章节例子3.1

Matd L = {{1, 1}};
L = L.Transpose();
Matd mu_Y{{0}, 
            {0}};
Matd D_Y{{2, 0}, 
            {0, 2}};
Matd D_delta{{2, 0}, 
                {0, 2}};
Matd D_Y_delta{{0, -1}, 
                {0, 0}};
Matd B{{-1, -1},
        {-1, 0}};
// D_YY * B.Transpose() + D_Y_delta
Matd tmp1 = D_Y * B.Transpose() + D_Y_delta;
Matd tmp2 = D_delta + B * D_Y_delta + D_Y_delta.Transpose() * B.Transpose() + B * D_Y * B.Transpose();
Matd tmp3 = tmp2.Inverse();
Matd Y_hat = mu_Y + tmp1 * tmp3 * (L - B * mu_Y);
cout << "tmp3(inverse):\n" << tmp3;
cout << "Y_hat :\n" << Y_hat;
/*
tmp3(inverse):
matrix:
value_type: d
size:       2 x 2
[[0.222222, -0.111111]
 [-0.111111, 0.222222]]
Y_hat :
matrix:
value_type: d
size:       2 x 1
[[-0.555556]
 [-0.222222]]
*/

自己的一些疑问

19-2-27

完成部分重构，添加了

operator()(size_t rowIndex, colIndex)
完成binary_operation对宏替换为函数

19-3-20

需要支持C++17

8. 动态规划优化后的链式乘法

1. 更新动态规划对矩阵乘法优化。方法为```OptimizedChainMultiply(Args&&... args)```。输入参数给他，就可以完成由动态规划优化的矩阵链式乘法。

void TestOptimizedChainMultiply() {

std::clock_t time_point_1;
std::clock_t time_point_2;
std::clock_t time_point_3;
using wj::Mati;
Mati a0 = Mati::Random(0, 10, 100, 500);
Mati a1 = Mati::Random(0, 10, 500, 10);
Mati a2 = Mati::Random(0, 10, 10, 75);
Mati a3 = Mati::Random(0, 10, 75, 55);
Mati a4 = Mati::Random(0, 10, 55, 10);
Mati a5 = Mati::Random(0, 10, 10, 100);
Mati a6 = Mati::Random(0, 10, 100, 74);
Mati a7 = Mati::Random(0, 10, 74, 45);
Mati a8 = Mati::Random(0, 10, 45, 200);
Mati a9 = Mati::Random(0, 10, 200, 100);
Mati a10 = Mati::Random(0, 10, 100, 200);
Mati a11 = Mati::Random(0, 10, 200, 700);

time_point_1 = std::clock();
auto result = a0 * a1 * a2 * a3 * a4 *
        a5 * a6 * a7 * a8 * a9 * a10 * a11;
time_point_2 = std::clock();
auto ret = wj::OptimizedChainMultiply(
        a0, a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11
);
time_point_3 = std::clock();
// 对两个矩阵进行比较
std::cout << std::boolalpha << (result == ret) << "\n";

double dur1 = static_cast<double>(time_point_2 - time_point_1) * 1000.;
double dur2 = static_cast<double>(time_point_3 - time_point_2) * 1000.;
std::fprintf(stdout, "Native use time:%f(ms)\n",(dur1 / CLOCKS_PER_SEC));
std::fprintf(stdout, "Optimezed use time:%f(ms)\n",(dur2 / CLOCKS_PER_SEC));
}

/**
 * 在单元测试中输出的结果：
 * 
TestOptimizedChainMultiply
15:27:47
144 ./TEST/unit_test.cpp
true
Native use time:687.500000(ms)
Optimezed use time:93.750000(ms)
*/

对于使用g++的时候，开启编译选项'-O2'（或者'-O3'）与否，将会大幅提升程序的性能。比如没有开启编译器优化选项的时候，直接用默认的-O0来编译，那么在上述例子的链式乘法中，从单元测试结果中得到耗时如下:

/**
 * 在单元测试中输出的结果：
 * 
TestOptimizedChainMultiply
15:27:47
144 ./TEST/unit_test.cpp
true
Native use time:687.500000(ms)
Optimezed use time:93.750000(ms)
*/

启动了不同级别优化选项之后：

/**
 * 优化选项 $g++ -std=c++17 -O1 ./test/unit_test.cpp  ./test/main.cpp -o a.out
 * 
TestOptimizedChainMultiply
14:59:16
144 ./TEST/unit_test.cpp
true
Native use time:109.375000(ms)
Optimezed use time:15.625000(ms)
*/

/**
 * 优化选项 $g++ -std=c++17 -O2 ./test/unit_test.cpp  ./test/main.cpp -o a.out
 * 
TestOptimizedChainMultiply
15:01:56
144 ./test/unit_test.cpp
true
Native use time:31.250000(ms)
Optimezed use time:15.625000(ms)
*/

/**
 * 优化选项 $g++ -std=c++17 -O3 ./test/unit_test.cpp  ./test/main.cpp -o a.out
 * 
TestOptimizedChainMultiply
15:03:07
144 ./test/unit_test.cpp
true
Native use time:31.250000(ms)
Optimezed use time:15.625000(ms)

其中 -O2 级别的优化最稳定，效率已经足够了。

为了更加稳定的测试，在测试案例中，使用进行1000次运算，明显时间少于很多，可能是因为流水线的影响：

/**
 * 平均时间十分惊人。。。
 * 
TestOptimizedChainMultiply
15:35:22
150 ./test/unit_test.cpp
true
Native use time:25.468750(ms)
Optimezed use time:4.078125(ms)
*/

对比python中的numpy：

# 在Python中同样进行相同规模的矩阵乘法
# 运算效率几乎一样
# 0.024140625

更新对Random的使用，使用了if constexpr来使得随机生成器合法，需要C++17.
添加了==运算符的重载，能够比较两个相同类型的Mat。不同类型是不能够比较的。

wujinggrt/matrix

矩阵库