This is an algorithm I made accompanying my Master's thesis. It is used to calculate topological invariants of manifolds given some parameters.
The main point of these algorithms is to calculate and verify a reciprocity formula, the formula looks like this:
$$
\frac{1}{|\det(H)|^{n-l/2}}\sum_{x \in (\mathbb{Z}^r/H(\mathbb{Z}^r))^n}\exp\left(\pi i x^T (L\otimes H^{-1}) x\right)
=\frac{1}{|\det(A)|^{m - r/2}}
\exp\left(\frac{i \pi}{4}\sigma(K)\sigma(L)\right)
\sum_{y \in (\mathbb{Z}^l/A(\mathbb{Z}^l))^m}
\exp\left(-\pi i y^T (K\otimes A^{-1}) y\right) \qquad (1)
$$
Where $L$ and $K$ are bilinear forms, i.e. symmetric matrices (also $K$ is even which means its diagonal elements are even) and $A$ and $H$ are the "invertible parts"
of $L$ and $K$. Also $n$ is the dimension of $L$, $m$ the dimension of $K$, $l$ is the rank of $L$ and $r$ is the rank of $K$.
This can be done with the reciprocity_formula function where you pass as arguments the matrices $L$ and $K$. The first output will be the left-hand-side of the equation above and the second output will be the right-hand-side.
however, its use can be much simpler than that:
At the base level it can compute gauss sums like: $$\sum_{n=0}^{p-1} \mathrm{exp}(i \pi q n^2 /p)$$
It can also do the following operations:
- Isolate the invertible part of a symmetric matrix (while keeping the symmetry) using the function split_matrix
- Calculate the cokernel of a symmetric matrix on the field of integers (i.e. the quotient group $\mathbb{Z}^n/L\mathbb{Z}^n$) with the function compute_cokernel
- Split the finite part of the above group into a direct sum of cyclic groups (using the same function)
- Calculate a linking form that corresponds to a given (linking) matrix (again with the same function)
- Calculate the integer linking matrix of a lens space L(p,q) (using Saveliev's method) with the function linking_mat_of_lens_space
- Perform the second Kirby move on symmetric (linking) matrices with the function K2
Very briefly, we can create a manifold by acting on a set of curves inside $S^3$. These curves are partially described by what is called the linking matrix, which is a symmetric matrix. Now there is a way of obtaining the homology of the manifold by looking at the linking matrix. Suppose that $L$ is an $n\times n$ linking matrix then the first homology group can be written as:
$$
H_1 = \langle G_1 ,..., G_n | L\cdot \mathbb{G} = 0 \rangle,
$$
where $\mathbb{G} = (G_1 , ... G_n)^T$ and $G_1,...,G_n$ are each a generator of $\mathbb{Z}$. In other words the first homology group will be given by the cokernel: $\mathbb{Z}^n/L\mathbb{Z}^n$
One thing this algorithm does is calculate the homology by calculating the above cokernel. It does that in two steps, first it isolates the invertible part from the non invertible part of the matrix using only the allowed moves (Kirby moves), bringing it into a form $A\oplus 0_{n-l}$ where $A$ is a symmetric $l \times l$ invertible matrix. Then it calculates the cokernel of $A$: $\mathbb{Z}^l/A\mathbb{Z}^l$.
If you are unfamiliar with the last expression it just means that points of $\mathbb{Z}^l$ are considered equivalent if they differ by a point in $A\mathbb{Z}^l$ (if $x-y = A(z)$ for some $z \in \mathbb{Z}^l$). Our group then would consist of only the inequivalent elements. There are many ways to depict it visually but one of the most natural ones is to consider the action of the matrix $A$ on the "fundamental cell", that is, the square or cube or n-dimensional cube that is formed by the basis vectors $(1,0,...0),(0,1,...,0)...(0,0,...,1)$. The n-paralelliped object that we will get this way would contain the elements of the group. Then the equivalence relation could be displayed as follows: whenever we try to move to an element that is outside the boundary of our area, we instead get teleported to the opposite side as if there was a portal connecting the two sides. We can visualize that in two dimensions with an example, let's say we had the matrix:
(4,2)
(2,4)
And we wanted to see how this group would look like, visually it would look like this:
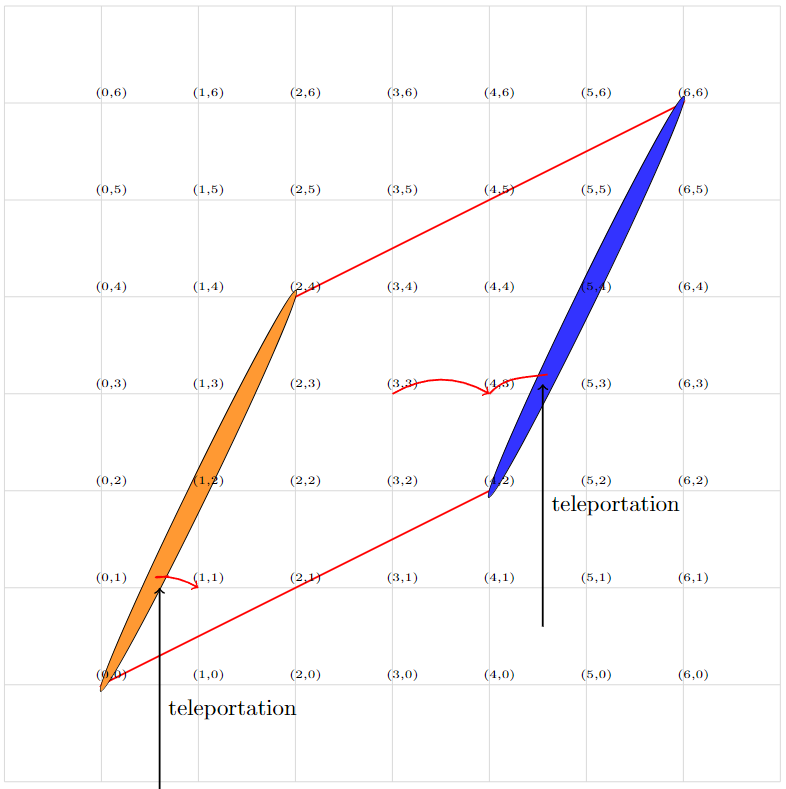
with the blue and orange parts acting as portals. Of course not shown explicitly in the figure there would also be "portals" connecting the top and bottom side of the shape. In order to find and calculate the properties of the above group we had to be able to do the following operations:
- Find a way to show which points are within the group. (done by is_within function)
- Find all the unique points that are in the group. (done by set_of_points_within function)
- Find the cyclic group decomposition of our group. (done by compute_cokernel and its subordinate functions)
For the last point we need to say that since $\mathbb{Z}^l/A\mathbb{Z}^l$ is a finite abelian group then it must have a decomposition into a direct sum of cyclic groups: $\mathbb{Z}_{p_1} \oplus \mathbb{Z}_{p_2} \oplus ... \oplus \mathbb{Z}_{p_k}$ where $p_i$ divides $p_{i+1}$. The essence of the algorithm is that it tries to find an element in group of order $p_k$ (meaning an element that if you add it to itself $p_k$ times it will be equivalent to $0$) and then uses it to generate a $\mathbb{Z}_{p_k}$ type group. Then it considers the original group quotient with the group we generated and repeats the process. The result should be a list of numbers that represent the coefficients of the $\mathbb{Z}_{p_i}$ groups. In addittion, we will get their generators for free.
As it is evident, another main function of this algorithm is the compute_cokernel one. It takes one input of a symmetric matrix and gives five outputs. These are:
- a list like the following $[p_k , p_{k-1},...,p_1]$
- the list of generators of the groups $\mathbb{Z}_{p_k} ... \mathbb{Z}_1$
- the linking form of the matrix in the basis of the above generators
- the corank of the matrix (i.e. the dimension minus the rank which corresponds to the number of (infinite) $\mathbb{Z}$ groups in its decomposition)
- the reduced matrix which is the invertible of the matrix after we separate invertible and non invertible
more will be added on the above explanation
The following is a topological invariant of our manifold
$$
\sum_{y \in (\mathbb{Z}^l/A(\mathbb{Z}^l))^m}
\exp\left(-\pi i y^T (K\otimes A^{-1}) y\right)
$$
where $A$ as we've seen before is the invertible part of the linking matrix and $K$ is a symmetrized coupling constant matrix. The main result of my Master's thesis is that we can relate the above invariant, through formula (1) to another Reshetikhin-Turaev-like invariant shown on the left hand side of the equation. The main function of this algorithm takes as input the linking matrix $L$ and the (even) symmetrized coupling constant matrix $K$ and outputs the left and right hand side of equation (1) in order to confirm it. Of course the formula is proven rigorously by Deloup and Turaev but it is nice to have numerical evidence.
More information will be added soon.
References to all of these are in my Master's Thesis and possibly a future paper.
