while current_iter < args.iterations:
""" E step """
for k in range(args.cluster_num):
if not args.tied:
P_Z_given_X[:, k] = lambdas[k] * N_X_given_muk_sigmak(train_xs, mus[k], sigmas[k])
else:
P_Z_given_X[:, k] = lambdas[k] * N_X_given_muk_sigmak(train_xs, mus[k], sigmas)
## Normalize to make the matrix row stochastic
P_Z_given_X = (P_Z_given_X.T / np.sum(P_Z_given_X, axis = 1)).T
## The number of datapoints belonging to each cluster
Num_ks = np.sum(P_Z_given_X, axis = 0)
""" M step: calculate the new mus and sigmas for each gaussian by applying above P_Z_given_X """
for k in range(args.cluster_num):
# lambdas update
lambdas[k] = 1.0 / N * Num_ks[k]
# mus update
total = np.matrix([0.0, 0.0])
for i in range(N):
# print("********P_Z_given_X[k][i]: ", P_Z_given_X[k][i])
temp2 = P_Z_given_X[i][k] * train_xs[i]
total += temp2
mus[k] = total / Num_ks[k]
x_minus_mus = np.matrix(train_xs - mus[k])
# sigmas updata
if not args.tied:
sigmas[k] = np.array(1.0 / Num_ks[k] * np.dot(np.multiply(x_minus_mus.T, P_Z_given_X[:, k]), x_minus_mus))
else:
sigmas = np.array(1.0 / Num_ks[k] * np.dot(np.multiply(x_minus_mus.T, P_Z_given_X[:, k]), x_minus_mus))
## likelihood computation for plotting
current_model = [lambdas, mus, sigmas]
# current_log_likelihood = np.sum(np.log(np.sum(P_Z_given_X, axis = 1)))
current_log_likelihood = average_log_likelihood(current_model, train_xs, args)
log_likelihoods.append(current_log_likelihood)
current_iter += 1
if not args.nodev:
ll_dev = average_log_likelihood(current_model, dev_xs, args)
print("iter %s dev log_likelihood: %s" % (str(current_iter), str(ll_dev)))
if ll_dev > best_ll:
best_ll = ll_dev
best_model = current_model
best_iter = current_iter
print("iter %s train log_likelihood: %s" % (str(current_iter), str(current_log_likelihood)))
1.1 Implemented the model initilization
1.2 Implemented both tied and full covariance
1.3 Implemented the logic of E and M step
1.4 Declared and implemented a function for computing Prob given the whole data matrix
1.5 Implemented logic using dev data to choose best model
1.6 Run different set of hyperparameters to choose best K(number of clusters) and I(number of iterations) for the data given
1.7 Wrote a function to plot the trend of average likelihood based on different input
1.8 Wrote a function to visualize the cluster
For lambdas: equal weights
For mus: randomly choose K data as the mus
For sigmas: just compute all the data's initial cov
The initialization is also important. Normally we choose the mus that not that close to each other.
I tried several times of same args. Every time the initialization are different because of random. However, the results were very similar finally. So we can see that the GMM is a good model with convergence.
Tied: (2,2) all used the same tied covariance Full: (args.cluster_num,2,2) k different covariance
I tried tied and full on the data and get quiet different results. Full cov are much better than the tied that the tied's corresponding ll even decrease with the iteration increases. Because there are two different gaussian model for each cluster. They don't need to be with total same cov. So the full cov will better help to train the data.
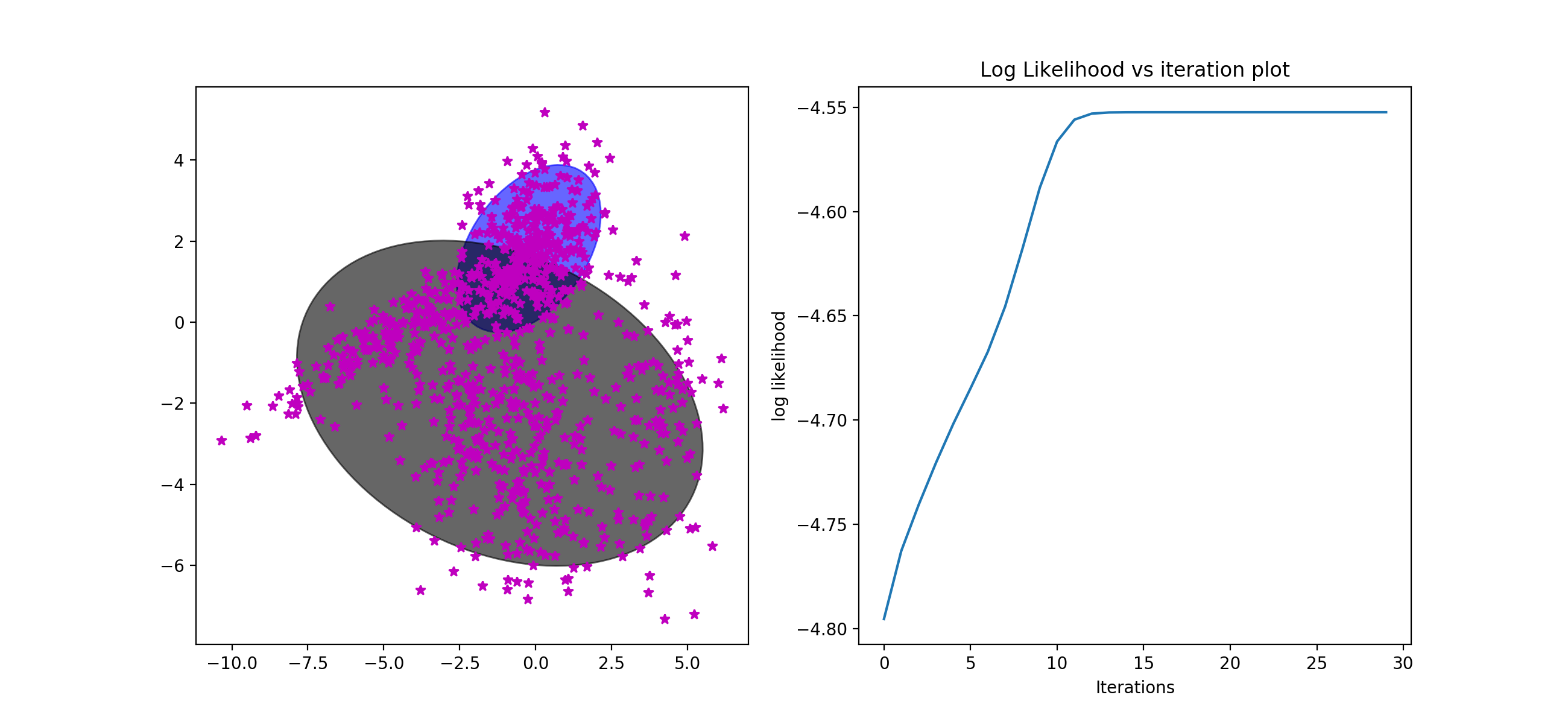
[Tied:]
best iterations: 26
Train LL: -4.6434310115250135
Dev LL: -4.573054852627335
Lambdas: 0.3309869716225309 | 0.3112811767125003 | 0.35773185166496907
Mus: -1.5656443 0.78612924 | 1.0287335 -3.423897 | -1.7639995 0.59269464
Sigma: 6.363095694082074 2.682985481094522 2.682985481094522 2.7155946906120434
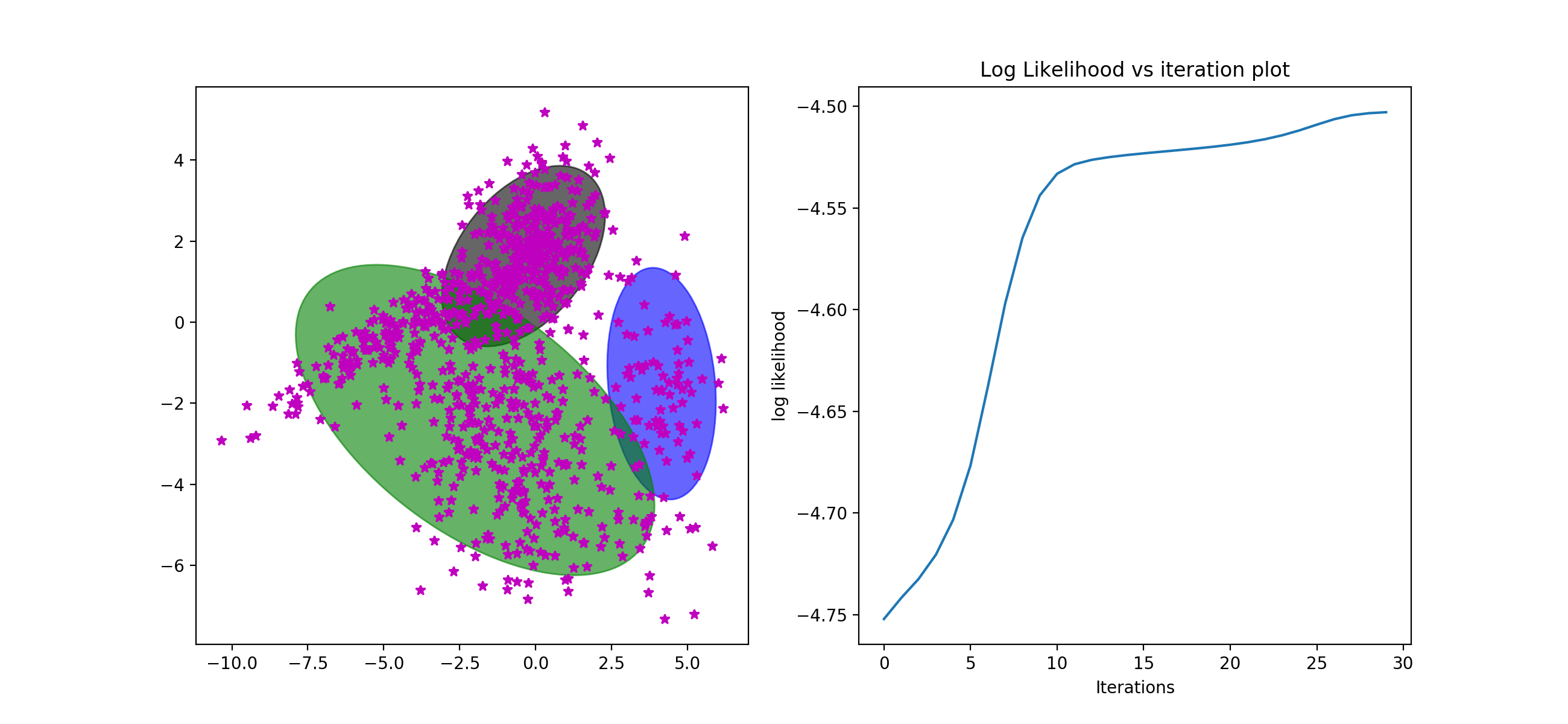
[Full]
best iterations: 30
Train LL: -4.408534943992172
Dev LL: -4.428588478374703
Lambdas: 0.21766690525109716 | 0.31900113086047127 | 0.46333196388843173
Mus: -4.0276423 -0.014956189 | -0.027472558 1.9194889 | 0.121785015 -2.5956209
Sigmas: 5.46446693090698 2.331650071097567 2.331650071097567 1.1739788583262072 | 1.0348618495556612 0.27430423408046867 0.27430423408046867 1.0982431865261826 | 7.332494377897124 -0.2298343619722579 -0.22983436197225796 3.815331550650095
Here all my computation are based on matrix. So I wrothe another function for computing Prob given the whole data matrix. It is also based on scipy.stats.multivariate_normal.
5.1 Inside the train_model function, I only focus on the best iteration. I kept track of each iteration and compare the average likelihood finally return the best one.
5.2 What's more, I also iterate K (number of clusters) and find the best hyperparameters set using different data. Here I run 30 iteration for each K and record the best ll on dev and final ll on training data. Every K run by 10 times to choose the best to avoid the influences of initialization.
Average log likelihood when K = 2: Train LL: -4.552393488272517 Dev LL: -4.652551176276237
Average log likelihood when K = 3: Train LL: -4.4555812491750695 Dev LL: -4.559940625476985
Average log likelihood when K = 4: Train LL: -4.356124260302845 Dev LL: -4.333912957848705
Average log likelihood when K = 5: Train LL: -4.3572362793207615 Dev LL: -4.319924483847427
Average log likelihood when K = 6: Train LL: -4.351551860156118 Dev LL: -4.3399043555224095
Average log likelihood when K = 7: Train LL: -4.3502621987954315 Dev LL: -4.334131138057317
Average log likelihood when K = 10: Train LL: -4.348944327376958 Dev LL: -4.326733513037062
From the log likelihood running on dev data, the best K is 5 and the I is 25.
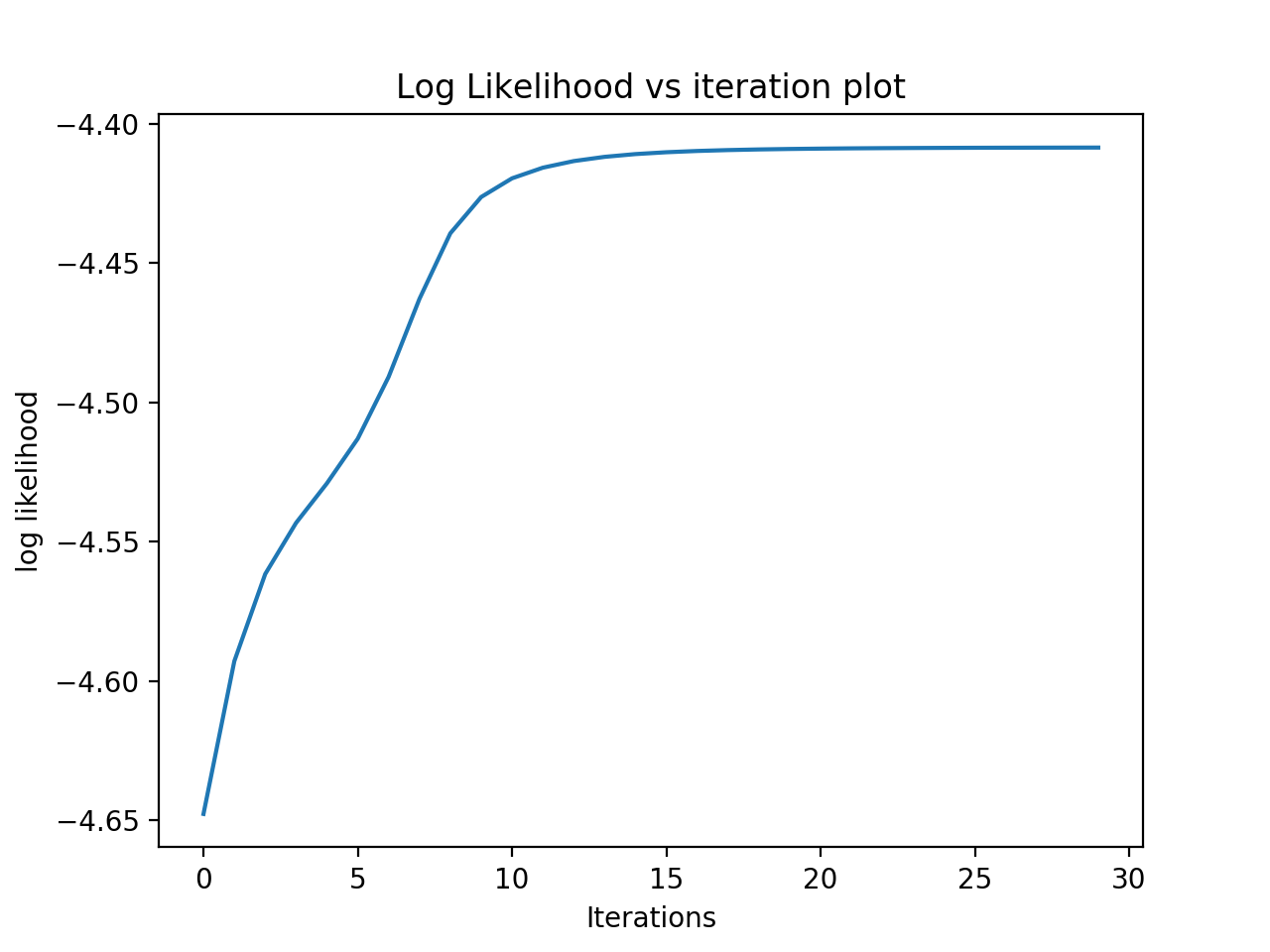
I run 30 iterations based on gaussian_smoketest_clusters.txt and get the result as follows. I also plotted them out in the graph. We can see that only after 13 iterations, the log likelihood changes very little after that. Because after rough 13 iterations, the data already converged.
Train LL: -4.552389712650888
Dev LL: -4.651680060110019 (iterations: 13)
Lambdas: 0.3687387825619876 | 0.6312612174380123
Mus: -0.22733368924786956 1.8138575955444145 | -1.1804852023826538 -1.999821958553207
Sigmas: 1.4037872999856293 0.5055214037437291 0.5055214037437291 1.0645775809832363 | 11.150122405331867 -1.8791714445924614 -1.8791714445924614 4.024144819215513
iter 1 dev log_likelihood: -4.822407754891544
iter 1 train log_likelihood: -4.795391728245874
iter 2 dev log_likelihood: -4.791350788360846
iter 2 train log_likelihood: -4.762766949823095
iter 3 dev log_likelihood: -4.771975507178417
iter 3 train log_likelihood: -4.740737480554617
iter 4 dev log_likelihood: -4.756540523994907
iter 4 train log_likelihood: -4.720579110423338
iter 5 dev log_likelihood: -4.745295422963848
iter 5 train log_likelihood: -4.701901681973038
iter 6 dev log_likelihood: -4.738633163842792
iter 6 train log_likelihood: -4.68478393104509
iter 7 dev log_likelihood: -4.733758549496411
iter 7 train log_likelihood: -4.667227130659346
iter 8 dev log_likelihood: -4.724011585604916
iter 8 train log_likelihood: -4.645511513798269
iter 9 dev log_likelihood: -4.703690367668828
iter 9 train log_likelihood: -4.617820499129099
iter 10 dev log_likelihood: -4.678640593759873
iter 10 train log_likelihood: -4.588617507202847
iter 11 dev log_likelihood: -4.660384618227316
iter 11 train log_likelihood: -4.566437683244976
iter 12 dev log_likelihood: -4.6529402562581
iter 12 train log_likelihood: -4.5559531940571265
iter 13 dev log_likelihood: -4.651596224688492
iter 13 train log_likelihood: -4.553060868246512
iter 14 dev log_likelihood: -4.651601584564344
iter 14 train log_likelihood: -4.552503917555793
iter 15 dev log_likelihood: -4.651679512219045
iter 15 train log_likelihood: -4.552409594600409
iter 16 dev log_likelihood: -4.651711254434139
iter 16 train log_likelihood: -4.5523935266410644
iter 17 dev log_likelihood: -4.6517180742149336
iter 17 train log_likelihood: -4.552390555662009
iter 18 dev log_likelihood: -4.65171585106752
iter 18 train log_likelihood: -4.552389929761206
iter 19 dev log_likelihood: -4.651711085496578
iter 19 train log_likelihood: -4.552389777183576
iter 20 dev log_likelihood: -4.651706055267584
iter 20 train log_likelihood: -4.552389734806648
iter 21 dev log_likelihood: -4.6517014562880785
iter 21 train log_likelihood: -4.552389721644571
iter 22 dev log_likelihood: -4.651697437514994
iter 22 train log_likelihood: -4.5523897170426
iter 23 dev log_likelihood: -4.651693974903871
iter 23 train log_likelihood: -4.552389715164737
iter 24 dev log_likelihood: -4.651691000741476
iter 24 train log_likelihood: -4.552389714239704
iter 25 dev log_likelihood: -4.651688444132804
iter 25 train log_likelihood: -4.552389713696417
iter 26 dev log_likelihood: -4.651686242847816
iter 26 train log_likelihood: -4.552389713336074
iter 27 dev log_likelihood: -4.651684344150161
iter 27 train log_likelihood: -4.552389713080554
iter 28 dev log_likelihood: -4.651682704269082
iter 28 train log_likelihood: -4.552389712893506
iter 29 dev log_likelihood: -4.651681286750287
iter 29 train log_likelihood: -4.552389712754631
iter 30 dev log_likelihood: -4.651680060110019
iter 30 train log_likelihood: -4.552389712650888