d3-geo

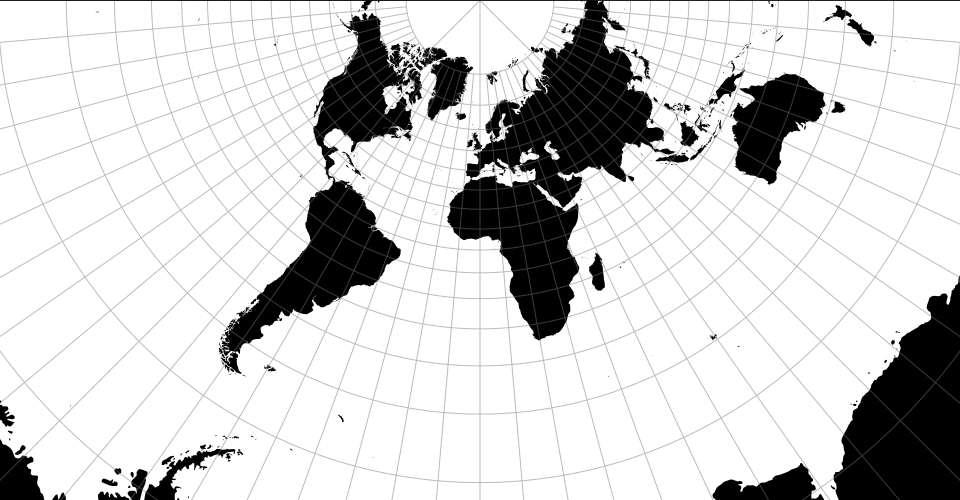
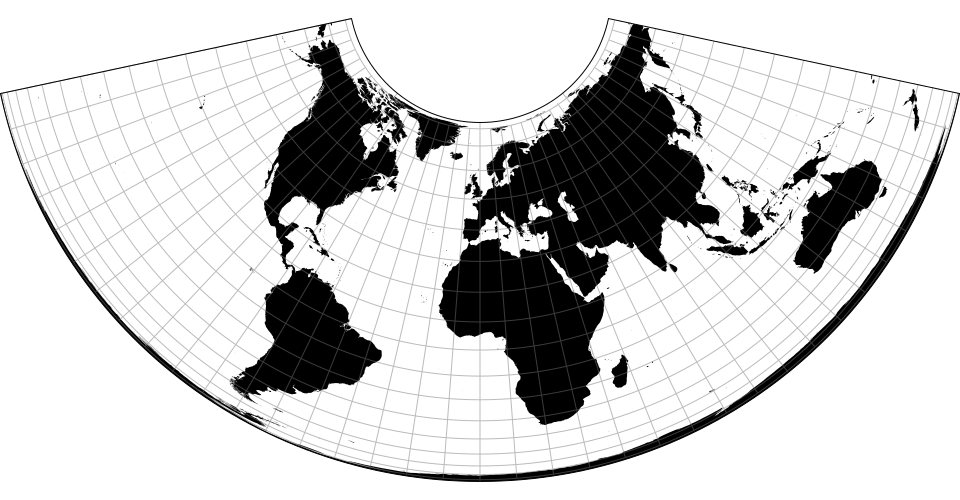
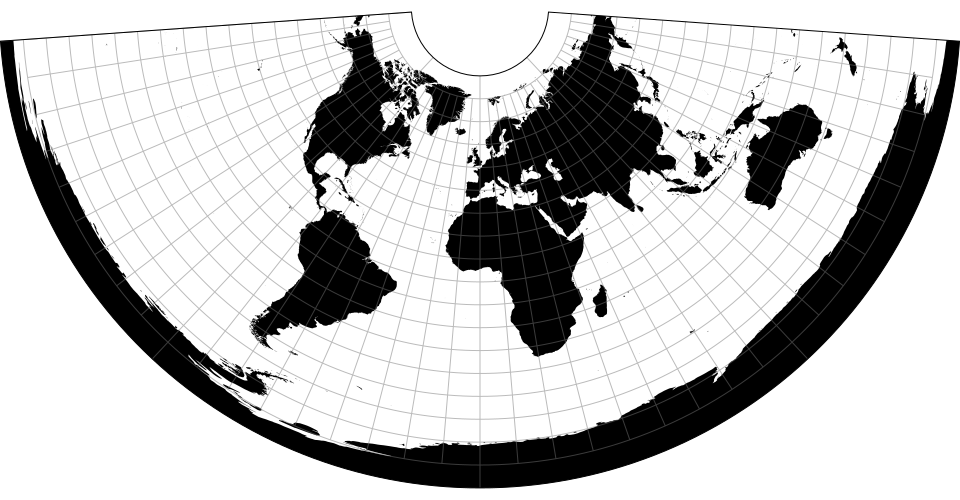
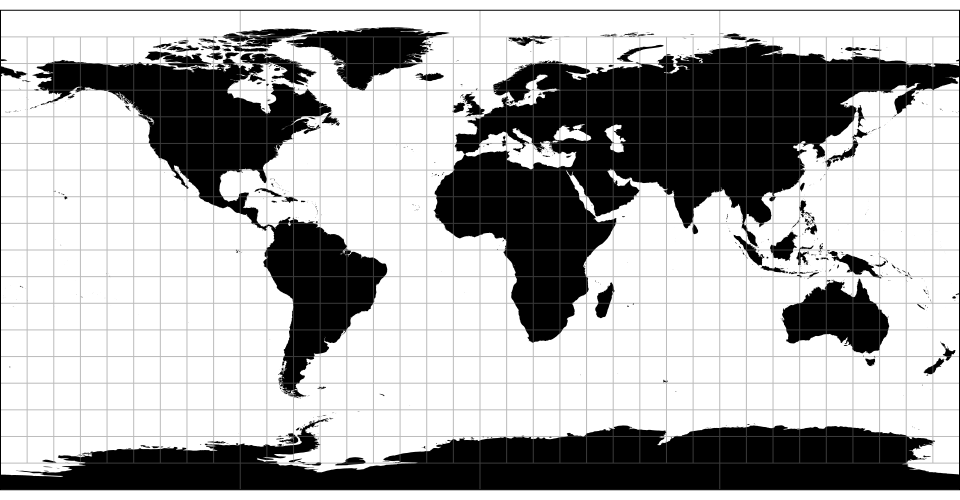
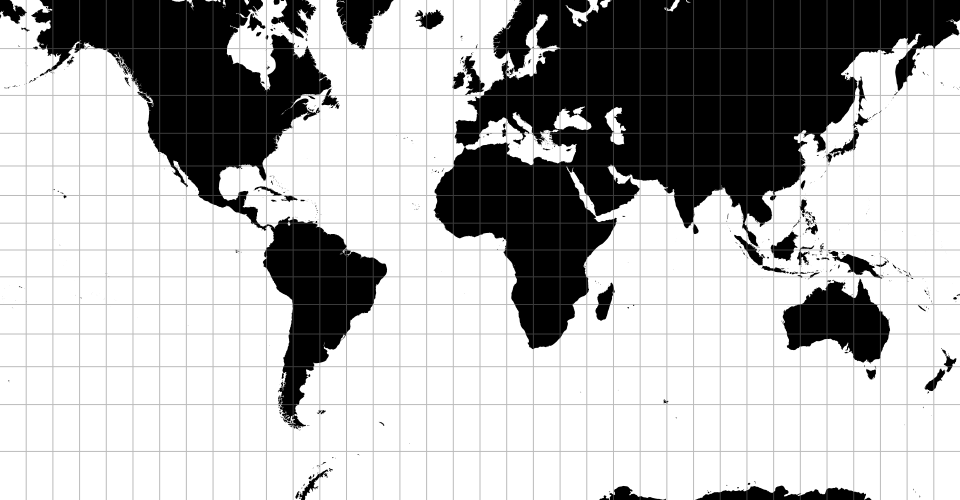
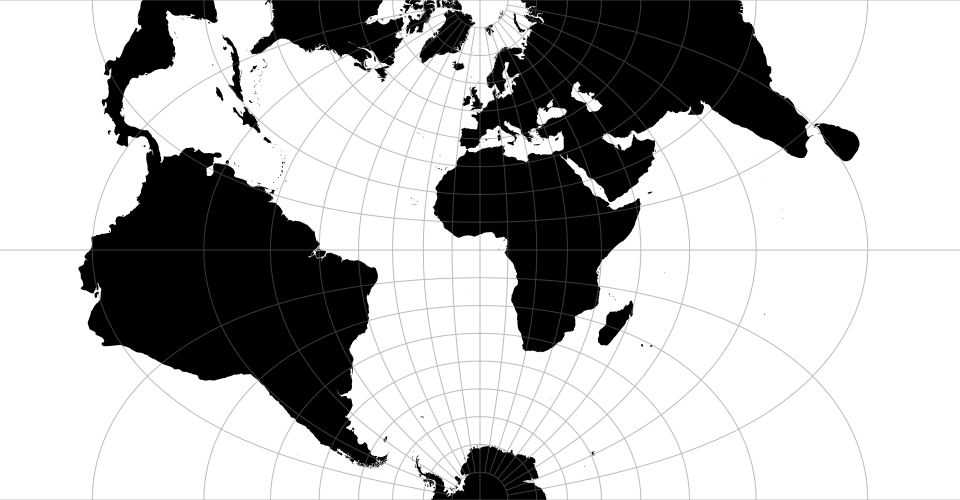
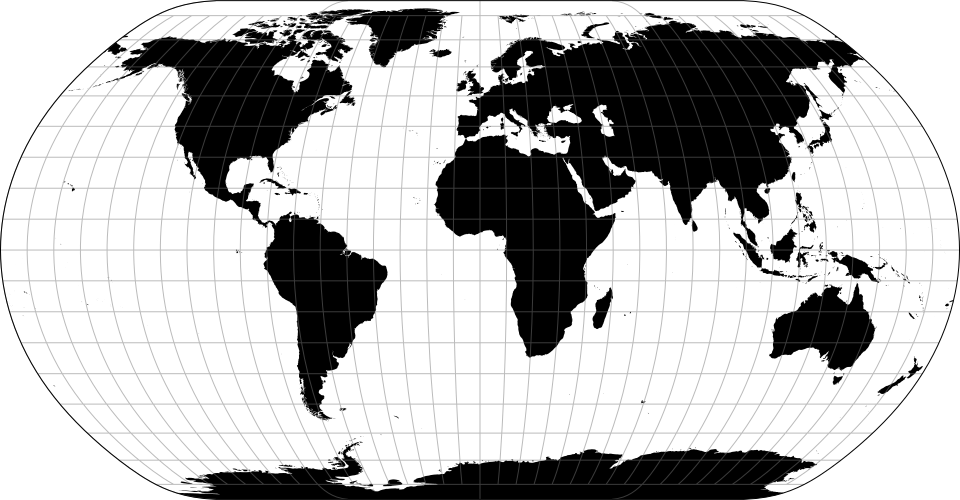
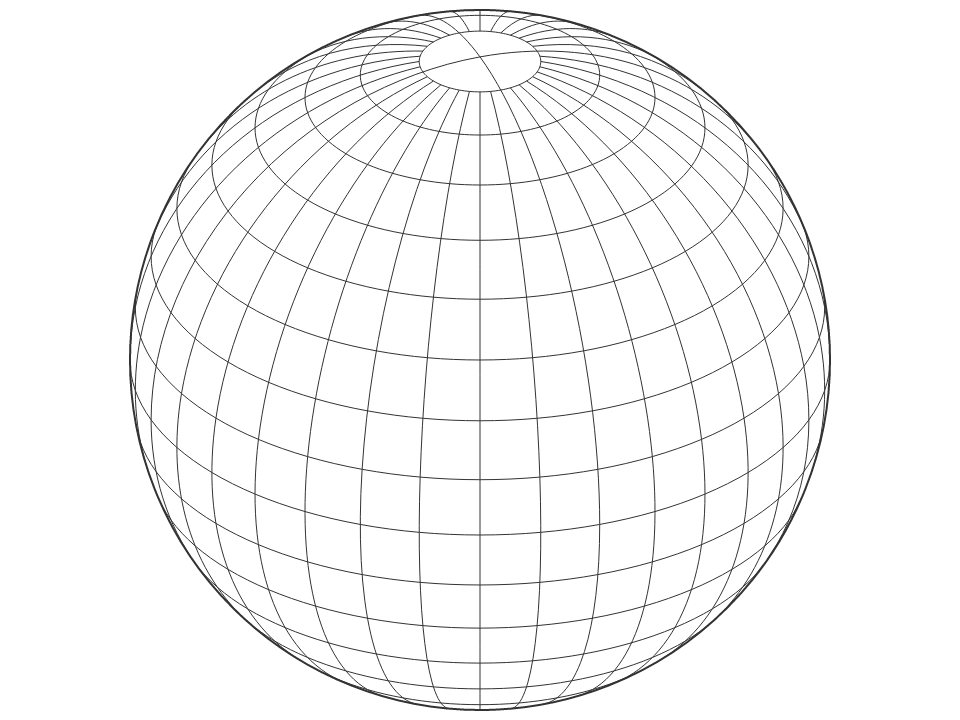
地图投影有时作为点的转换实现。比如球形墨卡托:

function mercator(x, y) {
  return [x, Math.log(Math.tan(Math.PI / 4 + y / 2))];
}

如果你的几何包含连续无限的点集时，这是一个合理的数学方法。然而，计算机并没有无限的内存，所以我们必须使用离散几何，比如多边形和折线!

离散几何使得从球面投影到平面更加困难。球面多边形的边缘是geodesics(测地线)great arc()的部分)，而不是直线。测地线投射到平面上，除了 gnomonic 之外所有的地图投影都是曲线，因此精确的投影需要沿每条弧插值。D3 使用 adaptive sampling(自适应采样)灵感来 line simplification method(线简化方法)，以平衡精度和性能。

多边形和折线的投影还必须处理球面与平面的拓扑差异。一些投影需要切割对向子午线的几何图形，而另一些投影则需要将几何图形 [裁剪为一great arc()](https://bl.ocks.org/mbostock/3021474)。

球面多边形还需要一个 winding order convention(缠绕顺序约定) 来确定多边形的哪边是内边: 小于半球的多边形的外环必须是顺时针方向, 而 larger than a hemisphere(大于半球的多边形的外环) 必须是逆时针的. 代表孔的内圈必须使用与其外圈的相反的环绕顺序。这种环绕规则也被 TopoJSON 和 ESRI shapefiles 采用。但是，它与 GeoJSON 的 RFC 7946 相反。(另请注意，标准 GeoJSON WGS84 使用平面的等距坐标，而不是球面坐标，因此可能需要 stitching 以去除对对向子午线的切割)。

D3的方法提供了很好的表现力: 你可以为你的数据选择正确的投影和样貌。D3 支持许多常见的投影以及特殊的地理投影. 更多信息可以参考工具制作指南.

D3 使用 GeoJSON 来表现地理特征. (也可以参考TopoJSON, 一种更加紧密的对 GeoJSON 的编码). 可以使用 shp2geo 将 shape 文件转为 GeoJSON, 这是 shapefile package 的一部分. 有关 d3-geo 和相关工具的介绍，请参阅 Command-Line Cartography.

Installing

使用 NPM: npm install d3-geo. 此外还可以下载 latest release. 可以直接从 d3js.org 以 standalone library 或作为 D3 4.0 的一部分直接引入. 支持 AMD, CommonJS 和基础的标签引入形式. 如果使用标签引入会暴露 d3 全局变量:

<script src="https://d3js.org/d3-array.v1.min.js"></script>
<script src="https://d3js.org/d3-geo.v1.min.js"></script>
<script>

var projection = d3.geoNaturalEarth1(),
    path = d3.geoPath(projection);

</script>

在浏览器中测试 d3-geo.

API Reference

Paths
Projections (Azimuthal, Composite, Conic, Cylindrical)
Raw Projections
Spherical Math
Spherical Shapes
Streams
Transforms
Clipping

Paths

地理路径生成器, d3.geoPath 与 d3-shape 很像: 给定一个 GeoJSON 或者特征对象，会生成一个 SVG 路径字符串，也可以将其渲染到 Canvas 上. 建议使用 Canvas 进行动态或者交互式投影以提高性能. 路径生成器可以与 projections 或 transforms 一起使用，或者可以直接将平面几何呈现到 Canvas 或 SVG 中.

# d3.geoPath([projection[, context]]) <>

使用默认的设置创建一个新的地理路径生成器. 如果指定了 projection, 则设置当前投影. 如果指定了 context 则设置当前当前上下文.

# path(object[, arguments…]) <>

渲染指定的 object, 可以是一个 GeoJSON 特征或者几何对象:

Point - 单个点.
MultiPoint - 一组点集.
LineString - 一组点集表示的连续的线.
MultiLineString - 组点集数组表示的多条线.
Polygon - 点集数组表示的多边形(可能有镂空).
MultiPolygon - 表示多个多边形的点集.
GeometryCollection - 一组几何对象.
Feature - 包含上述几何对象之一的特征.
FeatureCollection - 一组集合特征.

也支持类型为 Sphere, 在绘制地球轮廓时很有用; 球体没有坐标系. 任何额外的参数都会传递给 pointRadius 访问器.

显示多个特征时, 可以将其与特征集合结合:

svg.append("path")
    .datum({type: "FeatureCollection", features: features})
    .attr("d", d3.geoPath());

或者使用多个 path 元素:

svg.selectAll("path")
  .data(features)
  .enter().append("path")
    .attr("d", d3.geoPath());

多个 path 元素通常比单个 path 元素慢. 但是多个 path 在单独设置样式以及交互时很有用(比如点击和鼠标移入). Canvas 的渲染(可以参考path.context) 通常比 SVG 更快, 但是需要更多的精力去设置样式和交互.

# path.area(object) <>

返回指定的 GeoJSON 对象投影后的平面区域的面积(通常是平方像素). Point, MultiPoint, LineString 和 MultiLineString 面积为零. 对于 Polygon 和 MultiPolygon, 这个方法会首先计算外环的面积，然后减去镂空的面积. 这个方法遵循任何 projection 的裁剪; 参考 projection.clipAngle 和 projection.clipExtent. 这与 d3.geoBounds 的平面形式等价.

# path.bounds(object) <>

返回指定的 GeoJSON 对象投影后的平面包裹框(通常是像素). 包裹框被表示为一个二维数组: [[x₀, y₀], [x₁, y₁]], 其中 x₀ 是最小 x-坐标, y₀ 是最小 y-坐标, x₁ 是最大 x-坐标, and y₁ 是最大 y-坐标. 这对于缩放到特定的特性非常方便. (注意, 在投影平面坐标中, 最小纬度通常是最大 y 值, 而最大纬度通常是最小 y 值). 这个方法遵循任何 projection 的裁剪; 参考 projection.clipAngle 和 projection.clipExtent. 这与 d3.geoArea 的平面形式等价.

# path.centroid(object) <>

返回指定的 GeoJSON 对象投影后的平面质心(通常是像素). 这对于标记州或县的边界或显示符号非常方便. 例如非邻接统计地图可以以质心为中心进行缩放. 这个方法遵循任何 projection 的裁剪; 参考 projection.clipAngle 和 projection.clipExtent. 这与 d3.geoCentroid 的平面形式等价.

# path.measure(object) <>

返回指定的 GeoJSON 对象投影后的平面周长(通常是像素). Point, MultiPoint, LineString 和 MultiLineString 周长为零. 对于 Polygon 和 MultiPolygon, 这个方法会计算所有环的总长度. 这个方法遵循任何 projection 的裁剪; 参考 projection.clipAngle 和 projection.clipExtent. 这与 d3.geoLength 的平面形式等价.

# path.projection([projection]) <>

如果指定了 projection 则将当前投影设置为指定的投影. 如果没有指定 projection 则返回当前的投影, 默认为 null. null 投影表示一个恒等转换: 输入的集合不被计算, 而是直接在原始坐标中呈现. 这对于预投影来说省略了坐标计算因此速度更快, 或用于等矩形投影的快速绘制.

给定的 projection 通常是 D3 的内置地理投影; 但是任何暴露 projection.stream 函数的对象都可以被使用. 参考 D3 的 transforms 获取有关任意几何变换的更多例子.

# path.context([context]) <>

如果指定了 context 则将当前渲染上下设置为指定的 context 并返回当前路径生成器. 如果 context 为 null 则path generator 将返回 SVG 路径字符串; 如果 context 非 null 则路径生成器将调用指定上下文上的方法来呈现几何图形. 上下文必须实现 CanvasRenderingContext2D API 的以下子集:

context.beginPath()
context.moveTo(x, y)
context.lineTo(x, y)
context.arc(x, y, radius, startAngle, endAngle)
context.closePath()

如果没有指定 context 则返回当前的渲染上下文, 默认为 null.

# path.pointRadius([radius]) <>

如果指定了 radius 则将当前显示的 Point 和 MultiPoint 的半径设置为指定的数值. 如果没有指定 radius 则返回当前半径访问器, 默认为 4.5. 半径通常被指定为一个常数, 也可以被指定为一个返回数值的函数, 函数形式可以为每个特征单独计算半径值, 会传递 path generator 的参数. 例如, 如果你的 GeoJSON 数据有额外的数属性, 你可以使用访问器函数的形式去设置不同的半径; 也可以使用 d3.symbol 和 projection 来获取更大的灵活性.

Projections

投影可以将球面多边形几何映射为平面多边形几何. D3 提供集中标准投影的实现:

Azimuthal(方位投影)
Composite(合成投影)
Conic(圆锥投影)
Cylindrical(圆柱投影)

更多投影参考 d3-geo-projection. 你也可以使用 d3.geoProjection 或者 d3.geoProjectionMutator 实现自定义投影

# projection(point) <>

返回一个新的数组 [x, y](通常是像素) 来表示给定的 point 经过投影后的坐标. 给定的点必须是以度为单位的 [longitude, latitude] 形式. 如果给定的 point 没有定义投影位置则可能返回 null, 比如当点在投影的裁剪边界之外时.

# projection.invert(point) <>

根据指定的点坐标 [x, y](通常是像素) 计算出该点对应的经过投影前的以度为单位的坐标 [longitude, latitude](逆投影). 如果指定的点没有定义投影位置时可能返回 null, 例如当点在投影的裁剪边界之外时.

这种方法只定义在可逆投影上.

# projection.stream(stream) <>

为指定的输出 stream(流) 返回 projection stream(投影流). 任何输入的几何图形输出之前都会被投影. 一个典型的投影包括几个几何变换: 首先将输入几何图形转换为弧度, 三轴旋转, 裁剪或沿着对向子午线剪切, 最后通过自适应重采样, 缩放和平移投影到平面上.

# projection.preclip([preclip])

如果指定了 preclip 则将投影的球形裁剪设置为指定的裁剪函数并返回投影. 如果没有指定 preclip 则返回当前的预裁剪函数(参考 preclip).

# projection.postclip([postclip])

如果指定了 postclip, 则将投影的笛卡尔裁剪设置为指定的函数并返回投影. 如果没有指定 postclip 则返回当前的笛卡尔坐标裁剪(参考 postclip).

# projection.clipAngle([angle]) <>

如果指定了 angle 则以度为单位设置投影的裁剪角度并返回投影. 如果 angle 为 null 则切换为对向子午线裁剪而不是 small-circle 裁剪. 如果没有指定 angle 则返回当前的裁剪角度, 默认为 null. small-circle 独立于通过 projection.clipExtent 定义的视窗裁剪.

可以参考 projection.preclip, d3.geoClipAntimeridian, d3.geoClipCircle.

# projection.clipExtent([extent]) <>

如果指定了 extent 则将投影的视窗裁剪范围设置为指定的像素包裹框并返回投影. extent 以数组 [[x₀, y₀], [x₁, y₁]] 的形式指定, 其中 x₀ 为视窗的左侧坐标, y₀ 为顶部, x₁ 为右侧, y₁ 为底部坐标. 如果 extent 为 null 则不会执行视窗裁剪. 如果 extent 没有指定则返回当前的视窗裁剪范围, 默认为 null. 视窗裁剪独立于通过 projection.clipAngle 设置的 small-circle 裁剪.

参考 projection.postclip, d3.geoClipRectangle.

# projection.scale([scale]) <>

如果指定了 scale 则将投影的缩放因子设置为指定的值并返回投影. 如果没有指定 scale 则返回当前的缩放因子, 默认的缩放因子由具体的投影方式决定. 缩放因子与投影点之间的距离成线性关系; 但是在不同的投影中不同.

# projection.translate([translate]) <>

如果指定了 translate 则将投影的平移偏移量设置为指定的二元数组 [t_x, t_y] 并返回投影. 如果没有指定 translate 则返回当前的平移偏移, 默认为 [480, 250]. 平移偏移量决定了投影中心的像素坐标. 默认的平移偏移量将 ⟨0°,0°⟩ 放置在 960×500 的区域中心.

# projection.center([center]) <>

如果指定了 center 则将投影的中心设置为指定的以度为单位的 longitude 和 latitude 组成的二元数组 center 并返回投影. 如果没有指定 center 则返回当前的投影中心, 默认为 ⟨0°,0°⟩.

# projection.angle([angle]) <>

如果指定了 angle 则将投影后的旋转角度设置为指定的以度为单位的角度并返回投影. 如果没有指定 angle 则返回当前投影角度, 默认为 0°. 注意, 在渲染期间旋转(比如使用 context.rotate) 可能比通过投影旋转更快.

# projection.rotate([angles]) <>

如果指定了 rotation 则将投影的三轴球形旋转设置为指定的 angles, 角度必须是包含两个或三个元素的表示旋转角度的数组 [lambda, phi, gamma] 用以表示每个球面轴. (分别对应偏航，俯仰和横滚) 如果 gamma 没有指定则默认为 0. d3.geoRotation 也同理. 如果没有指定 rotation 则返回当前的角度默认为 [0, 0, 0].

# projection.precision([precision]) <>

如果指定了 precision 则将投影的自适应重采样阈值设置为指定的像素值并返回投影. 这个值对应 Douglas–Peucker 距离. 如果 precision 没有指定则返回投影当前的采样精度, 默认为 √0.5 ≅ 0.70710…

# projection.fitExtent(extent, object) <>

调整投影的 scale 和 translate 使给定的 GeoJSON object 适应在 extent 范围中. extent 以 [[x₀, y₀], [x₁, y₁]] 的形式指定, 其中 x₀ 为包裹框的左边界, y₀ 为上边界, x₁ 为右边界, y₁ 为下边界. 返回投影.

例如, 对 New Jersey State Plane projection 进行缩放和平移以将 GeoJSON 对象 nj 位于 960×500 的包裹框内, 并设置边距为 20:

var projection = d3.geoTransverseMercator()
    .rotate([74 + 30 / 60, -38 - 50 / 60])
    .fitExtent([[20, 20], [940, 480]], nj);

在确定了缩放和平移之后, 任何 clip extent 将会被忽略. 用来计算给定对象包裹框的 precision 计算的有效等级为 150.

# projection.fitSize(size, object) <>

projection.fitExtent 的便捷用法, 其中左上角坐标为 [0, 0]. 下面两个用法是等效的:

projection.fitExtent([[0, 0], [width, height]], object);
projection.fitSize([width, height], object);

# projection.fitWidth(width, object) <>

projection.fitSize 的便捷用法, 其中高度是根据对象的宽高比和宽度自动计算的.

# projection.fitHeight(height, object) <>

projection.fitSize 的便捷用法, 其中宽度是根据对象的宽高比和高度自动计算的.

Azimuthal Projections

方位投影把球体直接投射到平面上.

# d3.geoAzimuthalEqualArea() <>
# d3.geoAzimuthalEqualAreaRaw

等面积方位投影.

# d3.geoAzimuthalEquidistant() <>
# d3.geoAzimuthalEquidistantRaw

等距方位投影.

# d3.geoGnomonic() <>
# d3.geoGnomonicRaw

诺蒙尼日投影.

# d3.geoOrthographic() <>
# d3.geoOrthographicRaw

正交投影.

# d3.geoStereographic() <>
# d3.geoStereographicRaw

赤平投影.

Composite Projections

复合投影由多个投影组成. 复合投影具有固定的裁剪, 中心以及旋转, 并且复合投影不支持 projection.center, projection.rotate, projection.clipAngle, 和 projection.clipExtent.

# d3.geoAlbersUsa() <>

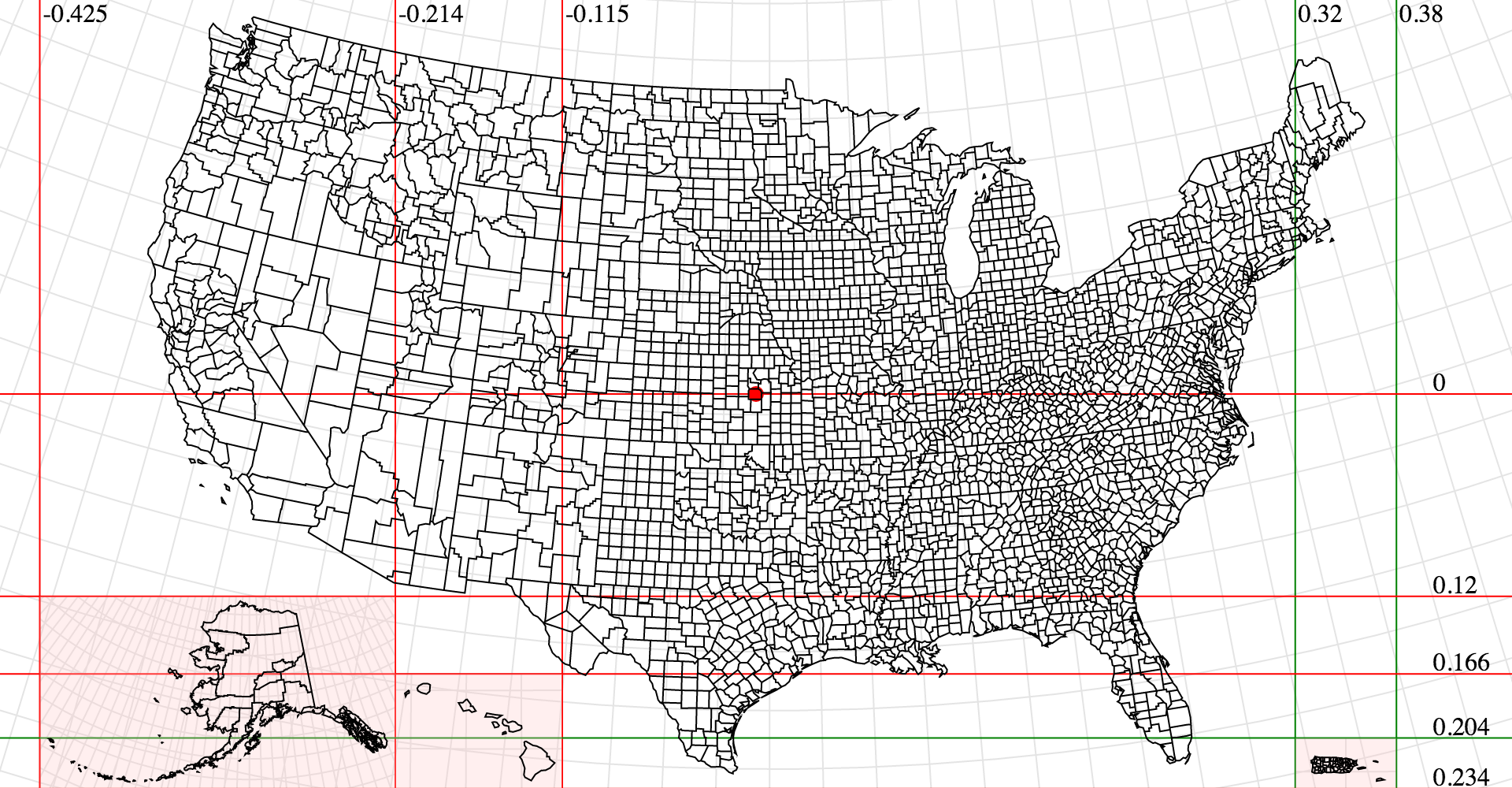
这是以美国为中心的三个 d3.geoConicEqualArea 组成的投影: d3.geoAlbers 用来投影较低的 48 个州, 圆锥等面积投影用来投影 Alaska 和 Hawaii. 请注意 Alaska 被缩小了: 相对被缩小到原来的 0.35 倍. Philippe Rivière 的这张图用来展示这个投影如何处理 Alaska 和 Hawaii：

See d3-composite-projections for more examples.

Conic Projections

圆锥投影将球体投射到圆锥上, 然后将圆锥展开到平面上. 圆锥投影有两条标准平行线.

# conic.parallels([parallels]) <>

在圆锥投影中定义地图布局的两个标准平行线.

# d3.geoAlbers() <>

Albers 的等面积圆锥投影. 这是以美国为中心的 d3.geoConicEqualArea.

# d3.geoConicConformal() <>
# d3.geoConicConformalRaw(phi0, phi1) <>

圆锥保角投影. 平行线默认为 [30°, 30°] 导致平顶. 参考 conic.parallels.

# d3.geoConicEqualArea() <>
# d3.geoConicEqualAreaRaw(phi0, phi1) <>

Albers 等面积圆锥投影. 参考 conic.parallels.

# d3.geoConicEquidistant() <>
# d3.geoConicEquidistantRaw(phi0, phi1) <>

圆锥等距投影. 参考 conic.parallels.

Cylindrical Projections

圆柱投影将球体投射到一个圆柱体上, 然后将圆柱体展开到平面上. Pseudocylindrical projections(伪圆柱投影) 是圆柱投影的延伸.

# d3.geoEquirectangular() <>
# d3.geoEquirectangularRaw

等矩形(圆柱)投影.

# d3.geoMercator() <>
# d3.geoMercatorRaw

球面墨卡托投影. 定义了默认的 projection.clipExtent: 世界被投射到一个正方形上, 裁剪到大约 ±85° 纬度.

# d3.geoTransverseMercator() <>
# d3.geoTransverseMercatorRaw

横向球面墨卡托投影, 定义了默认的 projection.clipExtent: 世界被投射到一个正方形上, 裁剪到大约 ±85° 纬度.

# d3.geoNaturalEarth1() <>
# d3.geoNaturalEarth1Raw

Natural Earth projection(自然地球投影) 是由 Tom Patterson 设计的伪圆柱投影. 它既不是等角也不是等角的, 但是看起来很吸引人, 像是一个缩小的世界.

Raw Projections

原始投影是一个用来实现自定义点转换功能的函数; 它们通常被传递给 d3.geoProjection 或 d3.geoProjectionMutator. 这个接口的暴露方便了相关投影的推导. 原始投影接收球面坐标 [lambda, phi] (弧度, 不是角度) 返回点坐标 [x, y], 通常是在以原点为中心的单位正方形中.

# project(lambda, phi)

计算给定以弧度为单位的点 [lambda, phi] 对应的投影后的无单位坐标 [x, y].

# project.invert(x, y)

project 的逆计算.

# d3.geoProjection(project) <>

根据指定的 raw projection 构造一个新的投影 project. project 函数以弧度为单位接收 longitude and latitude, 通常被称为 lambda (λ) and phi (φ), 返回二元数组 [x, y] 表示其单位投影. project 函数不需要缩放或平移点, 因为它们是通过 projection.scale, projection.translate, 和 projection.center 投影自动应用的. 同样的, 也不需要像投影那样执行任何球面旋转, 比如在投影之前使用 projection.rotate 进行球面旋转.

例如, 球面墨卡托投影可以实现为:

var mercator = d3.geoProjection(function(x, y) {
  return [x, Math.log(Math.tan(Math.PI / 4 + y / 2))];
});

如果 project 函数暴露 invert 方法, 则返回的投影会暴露 projection.invert.

# d3.geoProjectionMutator(factory) <>

根据指定的 raw projection factory 构造一个新的投影并返回一个当原始投影变化时调用的 mutate 函数. factory 必须返回一个原始投影. 返回的 mutate 函数返回一个投影函数. 例如, 圆锥投影通常有两个可配的平行线. 合适的 factory 比如 d3.geoConicEqualAreaRaw 应该为:

// y0 and y1 represent two parallels
function conicFactory(phi0, phi1) {
  return function conicRaw(lambda, phi) {
    return […, …];
  };
}

适用 d3.geoProjectionMutator 时, 你可以实现一个允许平行线改变的标准投影, 将内部使用的原始投影重新分配给 d3.geoProjection:

function conicCustom() {
  var phi0 = 29.5,
      phi1 = 45.5,
      mutate = d3.geoProjectionMutator(conicFactory),
      projection = mutate(phi0, phi1);

  projection.parallels = function(_) {
    return arguments.length ? mutate(phi0 = +_[0], phi1 = +_[1]) : [phi0, phi1];
  };

  return projection;
}

在创建可变投影时, 通常不会暴露 mutate 函数.

Spherical Math

# d3.geoArea(object) <>

返回指定的 GeoJSON 对象的球形区域的立体角. 等价于 path.area 的球面形式.

# d3.geoBounds(object) <>

返回指定 GeoJSON 对象的球面包围框. 包裹框以二维数组形式表示: [[left, bottom], [right, top]], 其中 left 为最小经度, bottom 为最小纬度, right 为最大经度, top 为最大纬度. 所有坐标都以度为单位. (注意, 在投影平面坐标中, 最小纬度通常是最大 y 值, 而最大纬度通常是最小 y 值) 等价于 path.bounds 的球面形式.

# d3.geoCentroid(object) <>

返回指定 GeoJSON 对象的球形质心. 等价于 path.centroid 的球面形式.

# d3.geoDistance(a, b) <>

以弧度为单位返回两点 a 和 b 之间的弧长. 每个点都必须被指定为以度为单位的二元数组的形式: [longitude, latitude]. 等价于两点之间计算 path.measure 的球面形式.

# d3.geoLength(object) <>

以弧度为单位返回指定 GeoJSON 对象的弧长. 如果是多边形则返回外环的周长加上任何内环的周长. 等价于 path.measure 的球面形式.

# d3.geoInterpolate(a, b) <>

在给定的两个点 a 和 b 之间返回一个插值函数. 每个点都必须被指定为以度为单位的二元数组的形式: [longitude, latitude]. 返回的插值函数接收单个参数 t, 其中 t 为从 0 到 1 的数值. t 为 0 时插值函数返回点 a, t 为 1 时插值函数返回点 b. 中间值沿着经过 a 和 b great arc()弧从 a 插值到 b. 如果 a 和 b 正相对应, 则选择任意great arc()弧.

# d3.geoContains(object, point) <>

判断一个点是否被包含在指定的 GeoJSON 对象中, 如果是则返回 true, 否则返回 false. 指定的点必须被指定为以度为单位的二元数组的形式: [longitude, latitude]. 如果 GeoJSON 为点或者多个点则启用精确测试, 如果是球则总是返回 true; 对于其他的几何类型, 则使用一个很小的阈值来判断是否被包含.

# d3.geoRotation(angles) <>

根据指定的 angles 返回一个旋转函数, 其中 angles 必须是一个二元或三元数值数组 [lambda, phi, gamma] 用来表示在每个球面轴上的旋转角度. (分别对应偏航，俯仰和横滚) 如果省略了 gamma 则默认为 0. 参考 projection.rotate.

# rotation(point) <>

以角度为单位返回将给定的点经过旋转后新的点: [longitude, latitude]. 指定的点必须以度为单位的二元数组形式: [longitude, latitude].

# rotation.invert(point) <>

根据指定的点返回该点经过旋转之前的点的坐标: [longitude, latitude]. 是 rotation 的逆运算, 同理指定的点也必须是以度为单位的二元数组形式.

Spherical Shapes

在生成 great arc(大圆弧的一部分)时, 只需要给 d3.geoPath 传入 GeoJSON LineString 对象即可. D3 的插值器使用大圆插值进行内部点插值, 因此不需要大圆弧生成器.

# d3.geoCircle() <>

返回一个新的圆生成器。

# circle(arguments…) <>

使用当前的 center, radius 和 precision 返回一个新的 GeoJSON 几何对象, 类型为 Polygon, 近似于球体表面上的一个圆. 任何参数都传递给访问器.

# circle.center([center]) <>

如果指定了 center 则将当前圆生成器的中心设置为指定的以度为单位的点: [longitude, latitude] 并返回圆生成器. 中心点可以指定为一个函数; 无论何时生成一个圆, 都会调用此函数, 并将传递给圆生成器的任何参数. 如果 center 没有被指定则返回当前的中心访问器, 默认为:

function center() {
  return [0, 0];
}

# circle.radius([radius]) <>

如果指定了 radius 则将当前圆生成器的半径设置为指定的角度(以角度为单位)并返回圆生成器. radius 可以指定为一个函数; 无论何时生成一个圆, 都会调用此函数, 并将传递给圆生成器的任何参数. 如果 radius 没有被指定则返回当前的半径访问器, 默认为:

function radius() {
  return 90;
}

# circle.precision([angle]) <>

如果指定的 precision 则将圆生成器的精度设置为指定的度并返回圆生成器. 精度可以指定为函数形式; 无论何时生成一个圆, 都会调用此函数, 并将传递给圆生成器的任何参数. 如果没有指定 precision 则返回当前的精度访问器, 默认为:

function precision() {
  return 6;
}

小圆不遵循大圆弧，因此生成的多边形只是一个近似, 指定一个较小的精确角度可以提高多边形的精度, 但也增加了生成和渲染它的成本.

# d3.geoGraticule() <>

构造用于创建经纬网的几何生成器: 一种由经线和纬线组成的均匀网格, 用于显示投影变形. 默认的经纬网的经纬线在 ±80° 之间每隔 10° 设置一条线. 对于极地地区则是 90°.

# graticule() <>

返回一个 GeoJSON MultiLineString 几何对象, 该对象表示此分划线的所有经纬线.

# graticule.lines() <>

返回一个 GeoJSON LineString 几何对象数组, 每个经线对应一个对象.

# graticule.outline() <>

返回一个 GeoJSON 多边形几何对象, 表示这个经纬网的轮廓, 也就是经纬网的边界.

# graticule.extent([extent]) <>

如果指定了 extent 则设置经纬网的经度和纬度边界. 如果没有指定 extent 则返回当前纬度边界, 默认为 ⟨⟨-180°, -80° - ε⟩, ⟨180°, 80° + ε⟩⟩.

# graticule.extentMajor([extent]) <>

如果指定了 extent 则设置经纬网的经度边界. 如果没有指定 extent 则返回当前经纬网经度边界, 默认为 ⟨⟨-180°, -90° + ε⟩, ⟨180°, 90° - ε⟩⟩.

# graticule.extentMinor([extent]) <>

如果指定了 extent 则设置经纬网的纬度边界. 如果没有指定 extent 则返回当前纬度边界, 默认为 ⟨⟨-180°, -80° - ε⟩, ⟨180°, 80° + ε⟩⟩.

# graticule.step([step]) <>

如果指定了 step 则设置经纬网的经度和纬度步长. 如果没有指定 step 则返回经纬网的纬度步长, 默认为 ⟨10°, 10°⟩.

# graticule.stepMajor([step]) <>

如果指定了 step 则设置经纬网的经度步长. 如果没有指定 step 则返回经纬网的经度步长, 默认为 ⟨90°, 360°⟩.

# graticule.stepMinor([step]) <>

如果指定了 step 则设置经纬网的纬度步长. 如果没有指定 step 则返回经纬网的经度步长, 默认为 ⟨10°, 10°⟩.

# graticule.precision([angle]) <>

如果指定了 precision 则以度为单位设置经纬网的精度. 如果没有指定 precision 则返回当前精度, 默认为 2.5°.

# d3.geoGraticule10() <>

一个方便的方法, 直接生成默认的 10° 的全球经纬网, 以 GeoJSON MultiLineString 对象形式返回。等价于:

function geoGraticule10() {
  return d3.geoGraticule()();
}

Streams

D3 使用一系列函数调用进行几何转换, 过渡过程中的中间值不被保存以最小化开销. 流必须实现多个方法来接收输入几何图形. 流本质上是有状态的; point 的定义取决于该点是否在 line 内, 同样地线与环的区别是由 polygon 决定的. 尽管被命名为 “流” 但是这些方法是被同步调用的.

# d3.geoStream(object, stream) <>

将指定的 GeoJSON 对象流到指定的投影流. 虽然 features 和 geometry 对象都支持作为输入, 但是流接口只描述几何形状, 因此其他特性属性对流来说是不可见的.

# stream.point(x, y[, z])

指示具有指定坐标 x 和 y (以及可选的 z )的点. 坐标系统未指定并且依赖于实现; 例如, projection streams 需要以角度为单位的球面坐标作为输入. 除了多边形和线上下文外, 点表示点对象(Point or MultiPoint). 在线或者多边形里, 点表示的是路径上的点坐标.

# stream.lineStart()

表示线或者多边形的起点. 在多边形里, 表示环的起点. 多边形的第一个环是外环, 通常是顺时针方向. 任何随后的环表示多边形上的孔, 通常是逆时针方向的.

# stream.lineEnd()

表示线或者多边形的终点. 在多边形里, 表示环的终点. 与 GeoJSON 不同, 环的冗余闭合坐标不通过 point 表示, 而是通过多边形中的 lineEnd 隐含. 因此, 给定的多边形输入:

{
  "type": "Polygon",
  "coordinates": [
    [[0, 0], [0, 1], [1, 1], [1, 0], [0, 0]]
  ]
}

将调用流的以下方法:

stream.polygonStart();
stream.lineStart();
stream.point(0, 0);
stream.point(0, 1);
stream.point(1, 1);
stream.point(1, 0);  // 结束，不会调用 stream.point(0, 0)
stream.lineEnd();
stream.polygonEnd();

# stream.polygonStart()

表示多边形的开始. 多边形的第一行表示外部环, 后面的任何一行表示内部孔.

# stream.polygonEnd()

表示多边形的结束.

# stream.sphere()

表示球(地球, 球心在 ⟨0,0,0⟩ 的单位球).

Transforms

变换是投影的推广. 变换实现了 projection.stream 并且可以被传递给 path.projection. 然而, 变换仅仅实现的是一个投影方法子集, 并且表示任意的几何变换, 而不仅仅是球面到平面的投影.

# d3.geoTransform(methods) <>

使用指定的方法对象定义一个任意的转换. 任何未定义的方法都将使用直通的方式将输入到输出流. 例如, 反转 y 维度(参考 identity.reflectY):

var reflectY = d3.geoTransform({
  point: function(x, y) {
    this.stream.point(x, -y);
  }
});

或者定义仿射矩阵变换:

function matrix(a, b, c, d, tx, ty) {
  return d3.geoTransform({
    point: function(x, y) {
      this.stream.point(a * x + b * y + tx, c * x + d * y + ty);
    }
  });
}

# d3.geoIdentity() <>

单位变换可用于缩放、平移和剪切平面几何图形. 它实现了 projection.scale, projection.translate, projection.fitExtent, projection.fitSize, projection.fitWidth, projection.fitHeight 和 projection.clipExtent.

# identity.reflectX([reflect])

如果指定了 reflect , 则设置是否在输出中反转 x 维度. 如果没有指定 reflect 则返回当前是否反转 x, 默认为 false.

# identity.reflectY([reflect])

如果指定了 reflect 则设置是否在输出中反转 x 维度. 如果没有指定 reflect 则返回当前是否反转 x, 默认为 false. 这在从标准的 spatial reference systems 转换时非常有用, 在此类系统中, y 方向是向上的, 而显示的时候比如 Canvas 和 SVG 则 y 是向下的.

Clipping

投影分两个阶段完成几何图形的切割或剪裁.

# preclip(stream)

预剪切发生在地理坐标中. 沿着180度经线切割. 或者沿着一个纬线切割是最常见的策略.

参考 projection.preclip.

# postclip(stream)

后期剪切发生在平面上, 当一个投影有一定的边界时, 例如一个将投影限制在一个矩形框中.

参考 projection.postclip.

裁剪函数以 projection stream 转换的形式实现. 预剪切操作在球面坐标上，以弧度为单位. 后剪接操作在平面坐标上，以像素为单位.

# d3.geoClipAntimeridian

一个剪切函数, 使跨越180度经线的几何图形流(线或多边形)被切成两半，每一边各一个. 通常用于预剪切.

# d3.geoClipCircle(angle)

生成一个剪切函数, 该函数转换流使得几何图形以围绕投影 center 的小半径角为界. 通常用于预剪切.

# d3.geoClipRectangle(x0, y0, x1, y1)

生成一个剪切函数, 该函数转换流使几何图形以矩形坐标框 [[x0, y0]， [x1, y1]] 为边界. 通常用于后期剪切.

xswei/d3-geo