/GAMMALAB-TASK

Neural Network Design Capability

Primary LanguagePython

GammaLab TASK--Neural Network Design Capability

根据特定的任务设计适合的网络结构，搭建出在限制条件下性能达标的网络

任务1:

找出一个序列中的最大值的起始位置

考察指标：
  1. inductive bias尽量小：epoch=1测试集的准确度达到98%
  2. 表达效率高：训练准确度达到96%所需的batches小于1000

任务2:

找出一个序列中连续三个数相加最大的子序列的起始位置

考察指标：
  1. inductive bias尽量小：epoch=1测试集的准确度达到98%
  2. 表达效率高：训练准确度达到96%所需的batches小于1000

任务3:

输入一个序列和一个标量N，找出该序列中连续N个数相加最大的子序列的起始位置

Constraints：
  1. batch = 32, lr=0.01, optimizer=Adam，epoch=1
  2. 为避免直接利用数字信息，将sequence和query统一embed到8维空间作为输入
  3. 因为建模随机性，只要5次有一次能超过指标即可
考察指标：
  1. 最后100个batch的平均准确率大于91%（bonus指标：大于95%）
  2. 100个batch的平均准确率稳定超过80%所需要的batch小于1100

任务4

训练：输入一个序列和一个标量N，连续N个数相加最大的子序列的起始位置为P1，同一P1的序列认为是一类
预测：输入一个序列和一个标量N，连续N个数相加最大的子序列的起始位置为P2，其中P1和P2的并集为空；将P2集合分成P2_1(target)和P2_2(distractor)，在P2_1=i中，选取两个（sequence，query），一个作为anchor，一个作为target混入distractor中，求target与anchor排名rank 1的平均准确度

Constraints
  1. 可跑多个epochs，可调参，注意regularization
  2. evaluation脚本：python3 evaluate.py embeddings.csv task4_test_label.csv，其中embeddings无header，无index，每行是一个embedding
考察指标
  1. 完成一个平均准确度超过50%的baseline
  2. 根据错误寻找一个优化点（optmization strategy方面的或是结构方面的优化点均可），完成并在baseline上有non-trivial的提升

任务5

输入为两个长度为N的序列，序列1中任意一个数a和序列2中任意一个数b，如果|a-b|=15，则认为a和b相似。两个序列中所有相似对（a，b）的个数是偶数时，label=0；奇数时，label=1

Hints：

设计一个alignment模块

Constraints：
  1. 结构设计，不用调参，固定batch = 32, lr=0.01, optimizer=Adam，epoch=1
  2. 为避免直接利用数字信息，将序列中的数字映射到8维空间作为输入
  3. 不设定硬性考察指标，请大家自行探索最优结构，最后进行测试集排行

任务6

一个序列由1和0组成，判断序列中1的个数是奇数还是偶数

Constraints：
  1. 结构设计，不用调参，固定batch = 32, lr=0.01, optimizer=Adam，epoch=1
  2. 为避免直接利用数字信息，将序列中的数字映射到8维空间作为输入
  3. 鼓励尝试各种结构，不过至少一种结构是基于RNN的
  4. 测试集accuracy达到100%
挑战任务

判断一个序列中奇数的个数是奇数还是偶数

任务7

设计网络结构，预测二维物体的对称性和空隙率

空隙率：二维物体本身像素点数/经过形态学闭运算后像素点数
对称性：左右对称性

说明:虽然这个任务大家听的比较多了，但还是值得亲手做一做

Constraints：
  1. 设计两个不同的网络结构分别预测对称性和空隙率
  2. 两个任务acc均大于95%，依据测试集acc进行排名，作为年终考评参考

任务8

设计网络结构，反转一个变长序列（最大长度N=20），即246910000反转为196420000，其中1-9为需要反转的有效字符，0为补位字符

考核点：
  1. 序列长度很长时，如何记住前序信息
  2. output structure是序列的优化方法
Constraints：
  1. 结构设计，不用调参，固定batch=32， lr=0.02, optimizer=Adam, epoch=1
  2. 将序列中的数字映射到8维空间作为输入
  3. 禁止直接将input与output层相连

年终竞赛

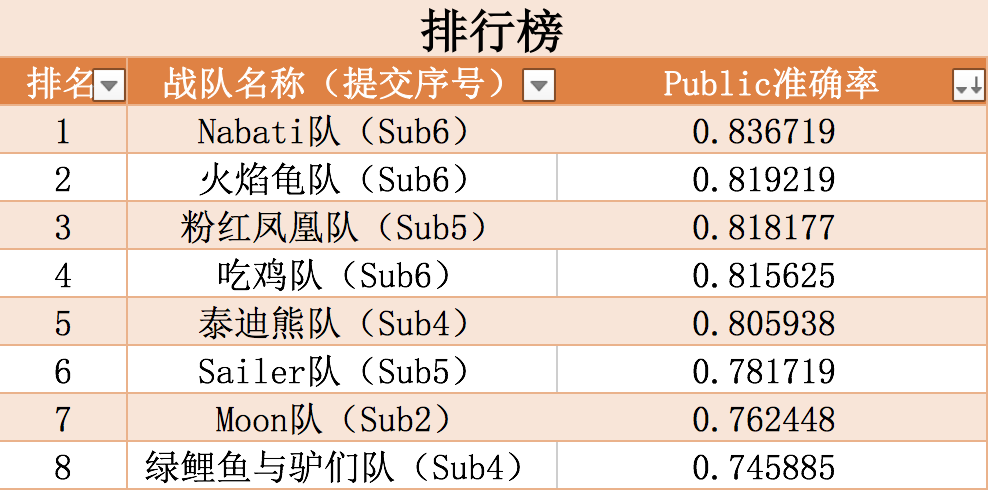
快乐集成一起吃鸡 很幸运碾压性优势获得第一

TASK RANK

TODO

  • Update task1 run.py
  • Update task2.py
  • Update task3.py
  • Update task4.py
  • Update task5.py
  • Update task6.py
  • Update task7.py
  • Update task8 run.py
  • Update 年终竞赛.py