githut
(1)Ceres Solver
(2)Ceres-Solver学习笔记(1)
(3)Ceres-Solver学习笔记(2)
(4)Ceres-Solver学习笔记(3)
(5)Ceres-Solver学习笔记(4)
(6)Ceres-Solver学习笔记(5)
(7)Ceres-Solver学习笔记(6)
(8)Ceres-Solver学习笔记(7)
(9)Ceres-Solver学习笔记(8)
(10)Ceres-Solver学习笔记(9)
$${\arg \min}_{x} f(x)=\frac{1}{2}(10-x)^{2}\tag{1}$$
步骤
(1)编写CostFunction结构体。必须重载运算符(),必须使用模板类型,所有输入参数和输出参数都使用模板类型。
(2)构造一个求解非线性最小二乘法的Problem来进行未知数求解。
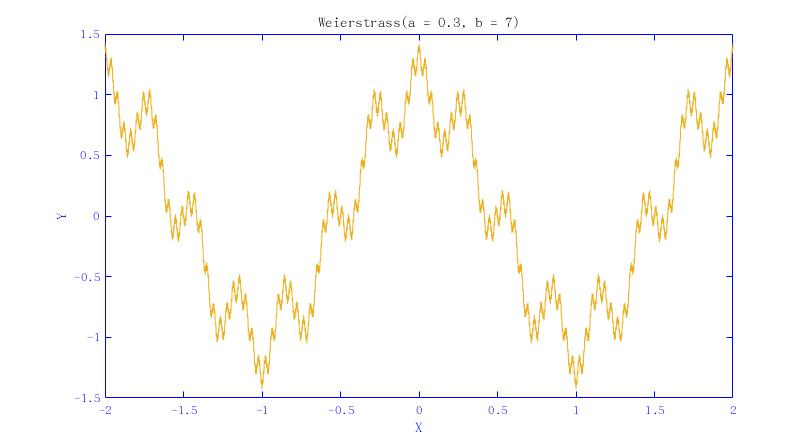
(1)魏尔斯特拉斯函数(Weierstrass function)
$$f(x)=\sum_{n=0}^{N}a^{n}cos(b^{n} \pi x)\tag{2}$$
其中$0<a<1$,$b$为正奇数,且满足$ab>1+\frac{3}{2} \pi$
(2)Weierstrass图像绘制
(3)步骤
(3.1)构造数据。设置参数$a=0.3, b=7, n=200$ 。
(3.2)编写CostFunction结构体。
(3.3)构造一个求解非线性最小二乘法的Problem来进行未知数求解。
(4)总结
(4.1)利用ceres无法对非线性函数进行曲线拟合,如魏尔斯特拉斯函数。原因包括两点:函数无法进行微分求解和初始点难以选取。
(4.2)此处改为ceres对$y=e^{ax^{2}+b}$函数进行曲线拟合,其中 $a=0.3, b=0.1$ 。该函数图如下所示:
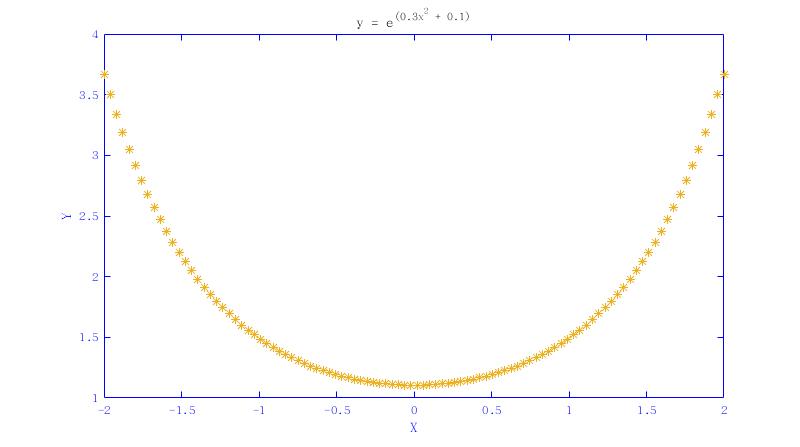
(4.3)可以采用三种方法对问题进行求解,即:在进行Problem构建时,采用AutoDiffCostFunction或NumericDiffCostFunction进行数值微分求解;当无法使用模板来创建costfunctor时,继承SizedCostFunction类来实现Problem。
(1)共线方程
$$\begin{equation} \begin{split} \left{ \begin{array}{} x-x_{0}=- f\frac{a_{1}(X-X_{s})+b_{1}(Y-Y_{s})+c_{1}(Z-Z_{s})}{a_{3}(X-X_{s})+b_{3}(Y-Y_{s})+c_{3}(Z-Z_{s})}, & \ y-y_{0}=-f \frac{a_{2}(X-X_{s})+b_{2}(Y-Y_{s})+c_{2}(Z-Z_{s})}{a_{3}(X-X_{s})+b_{3}(Y-Y_{s})+c_{3}(Z-Z_{s})} \end{array} \right. \end{split}\tag{3} \end{equation}$$
其中$x_{0}, y_{0}, f$已知,$abc$为旋转矩阵,可以利用$\phi, \omega, \kappa$表示如下:
$$\begin{equation} \begin{split} \left{ \begin{array}{} a_{1}=cos\phi cos\kappa -sin\phi sin\omega sin\kappa, & \ a_{2}=-cos\phi sin\kappa -sin\phi sin\omega cos\kappa, & \ a_{3}=-sin\phi cos\omega, & \ b_{1}=cos\omega sin\kappa, & \ b_{2}=cos\omega cos\kappa, & \ b_{3}=-sin\omega, & \ c_{1}=sin\phi cos\kappa +cos\phi sin\omega sin\kappa, & \c_{2}=-sin\phi sin\kappa +cos\phi sin\omega cos\kappa, & \ c_{3}=cos\phi cos\omega \end{array} \right. \end{split}\tag{4} \end{equation}$$
(2)步骤
(2.1)读入数据,格式为$(x, y, X, Y, Z)$ 。前2维像素坐标—单位$mm$ ,后三维代像坐标—单位$m$ 。
(2.2)编写CostFunction结构体。
(2.3)构造一个求解非线性最小二乘法的Problem来进行未知数求解。
(3)运行结果
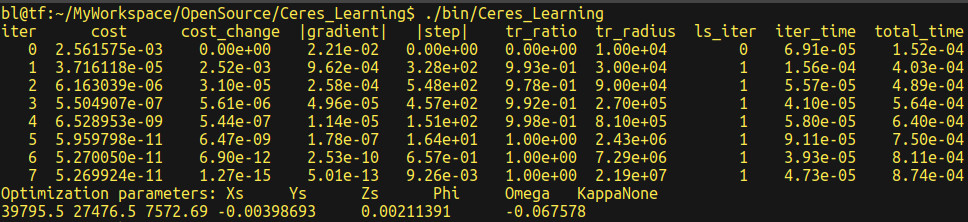
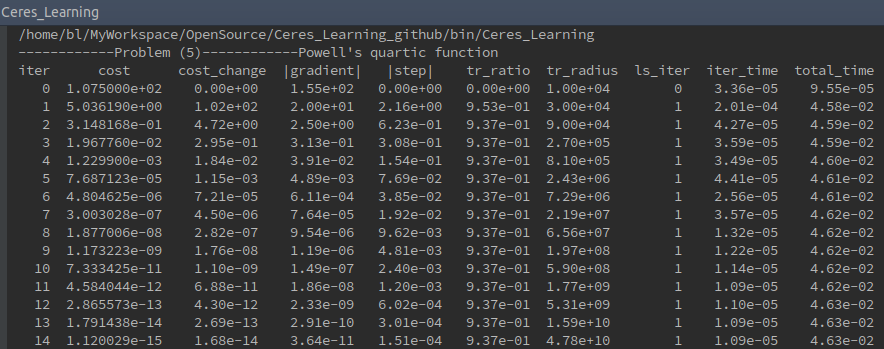
1.4 Powell's Quartic Function
(1)数学表达式
$$f(X)=\left(x_1+10x_2\right)^2+5\left(x_3-x_4\right)^2+\left(x_2-2x_3\right)^4+10\left(x_1-x_4\right)^4\tag{5}$$
其中:
$\bullet -10\leq x_i\leq 10, i=1,2,3,4$
$\bullet f_{min}(X^*)=0$
$\bullet x^*_i=0$
(2)Powell's Quartic Function分解
$$\begin{equation} \begin{split} f_{1}(x)&=x_{1}+10x_{2} \ f_{2}(x)&=\sqrt{5}(x_{3}-x_{4}) \ f_{3}(x)&=(x_{2}-2x_{3})^{2} \ f_{4}(x)&=\sqrt{10}(x_{1}-x_{4})^{2} \ F(x)&=[f_{1}(x), f_{2}(x), f_{3}(x), f_{4}(x)] \end{split} \end{equation}\tag{6}$$
(3)最优化问题数学描述
$${\arg \min}_{x} \frac{1}{2} |F(x)|^{2}\tag{7}$$
(4)步骤
(4.1)编写CostFunction结构体。
(4.2)构造一个求解非线性最小二乘法的Problem来进行未知数求解。
(5)运行结果
(1)BA数据集
Bundle Adjustment in the Large
备注:此处使用Ladybug Dataset:problem-49-7776-pre.txt.bz2
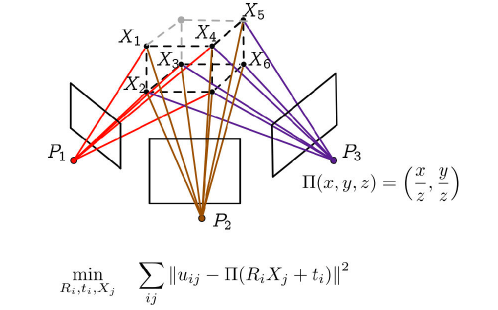
(2)BA问题
ceres solver学习之bundle adjustment
(3)步骤
(3.1)读取problem-49-7776-pre.txt.bz2数据。
(3.2)编写CostFunction结构体。
(3.3)构造一个求解非线性最小二乘法的Problem来进行未知数求解。
(4)运行结果