The following R code demonstrates how to implement the method proposed in Li et al. (2022) [1].
source('source_fQR.R')
### examples to visualize simulated data ------
n.tp = 100
sim_data <- sim.fQR(n.sub = 100, n.tp = n.tp, eigen.basis = "legendre.polynomials")
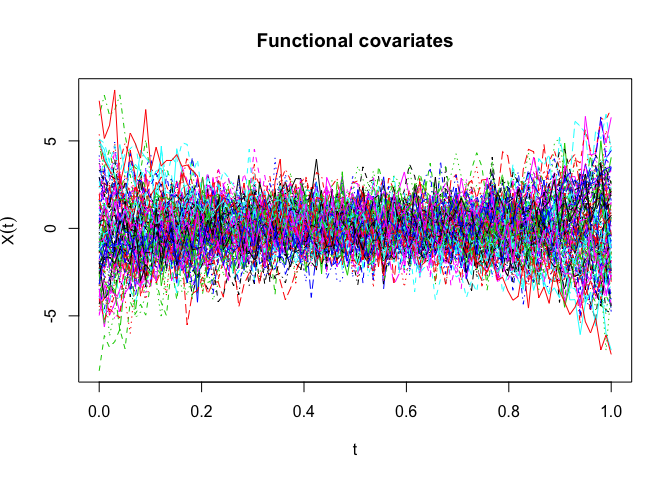
## Functional covariates:
## eigen.value = 1 0.5 0.25
## eigen.function = legendre.polynomials
matplot(x = seq(from = 0, to = 1, length = n.tp), t(sim_data$X), type="l",
xlab = expression(t), ylab = expression(X(t)), main = "Functional covariates") ### real data example using the bike rental data set ----
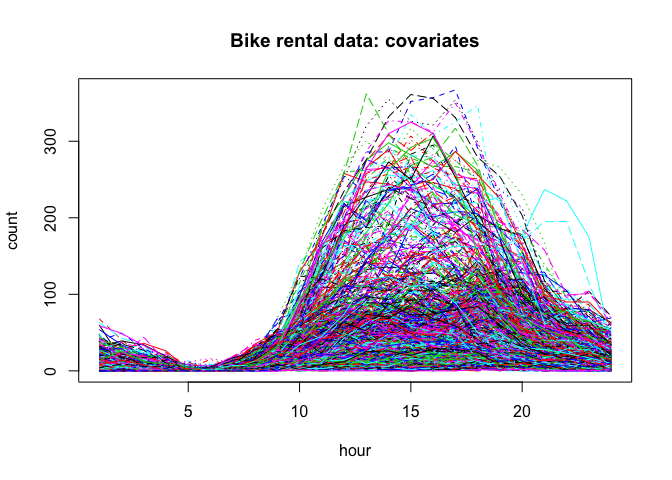
load("bike_data.RData")
matplot(x = 1:24, t(X), type="l",
xlab="hour", ylab="count", main = "Bike rental data: covariates")taus = c(0.8,0.825,0.85,0.875,0.9)
ret = fQR(Y, X, taus = taus, pve = 0.99)
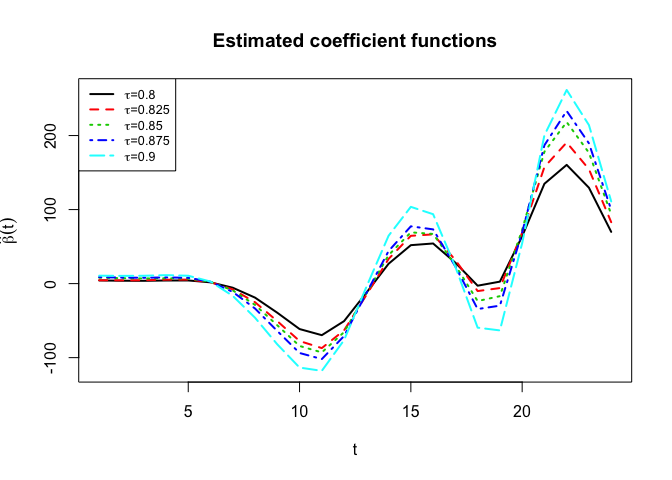
# plot beta.hat for each quantile level
matplot(x = 1:24, ret$beta.hat,
type = "l", col = 1:length(taus), lty = 1:length(taus), lwd = 2,
xlab=expression(t), ylab = expression(hat(beta)(t)),
main = "Estimated coefficient functions")
legend("topleft", legend = c(expression(paste(tau,"=0.8")),
expression(paste(tau,"=0.825")),
expression(paste(tau,"=0.85")),
expression(paste(tau,"=0.875")),
expression(paste(tau,"=0.9"))),
col = 1:length(taus), lwd=rep(2, ret$K),lty = 1:length(taus), cex=0.8)# pvalue for constancy slope test
ret$pvalue
## [1] 0.2991717
### Composite Quantile regression ----
# Method 1: QAE
b.QAE = apply(ret$coef[-1,],1,mean)
beta.QAE = ret$x.fpca$efunctions %*% b.QAE
# Method 2: CRQ
CRQ = crq.fit.func(Y,ret$x.fpca$scores,taus)
a.CRQ = CRQ[1,]
b.CRQ = CRQ[-1,1]
beta.CRQ = ret$x.fpca$efunctions %*% b.CRQ## focus on the 0.9th quantile
coef.matrix <- cbind(RQ = ret$coef[-1, ret$K], b.QAE, b.CRQ)
beta.matrix <- ret$x.fpca$efunctions %*% coef.matrix
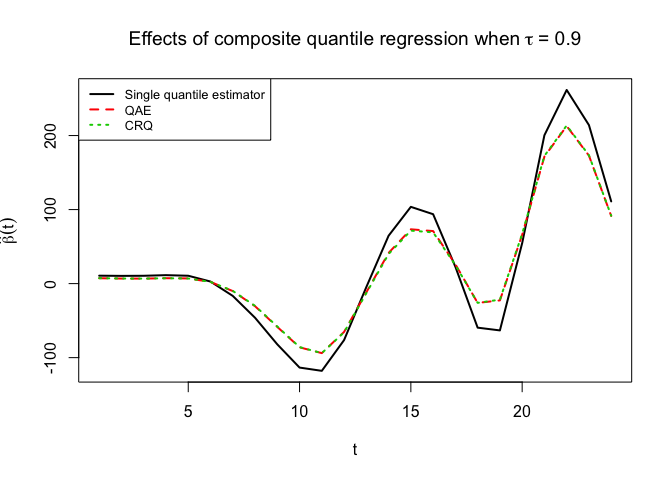
# plot beta.hat for each quantile level
matplot(x = 1:24, beta.matrix,
type = "l", col = 1:3, lty = 1:3, lwd = 2,
xlab=expression(t), ylab = expression(hat(beta)(t)),
main = expression("Effects of composite quantile regression when" ~ tau ~ "= 0.9"))
legend("topleft", legend = c("Single quantile estimator",
"QAE", "CRQ"),
col = 1:3, lwd=rep(2, 3),lty = 1:3, cex=0.8)
[1] Li, M., Wang, K., Maity, A. and Staicu, A.M. (2022). Inference in Functional Linear Quantile Regression. Journal of Multivariate Analysis, 190, 104985.
[2] The bike data is recorded by the Capital Bikeshare System (CBS), which is available at http://capitalbikeshare.com/system-data.