LibMOON: A Gradient-based MultiObjective OptimizatioN Library in PyTorch

LibMOON is an open-source library built on PyTorch for gradient based MultiObjective (MOO). See the latest documentation for detailed introductions and API instructions.

Star or fork us on GitHub — it motivates us a lot!

News

[Sep 26 2024] LibMOON paper is accepted to NeurIPS 2024.
[Aug 27 2024] Added support for LoRA-PSL (ICML 2024). Many thanks to Weiyu Chen for his contribution.
[June 20 2024] Supports most popular gradient-based methods: MGDAUB, Random, EPO, PMGDA, Aggregation-based methods, PMTL, HVGrad, MOOSVGD ...
[April 20 2024] Supports PMTL (NeurIPS 2019), HvGrad (EMO 2022). Many thanks for Dr. Xi Lin's contribution and helpful communications from Dr. Hao Wang.
[March 17 2024] Supports three MOBO-PSL methods. Many thanks to Liang Zhao's contribution.
[March 10 2024] Supports hypernetwork-based Pareto set learning methods.

1. LibMOON Supported Problems

1.1 Synthetic Problems

LibMOON supports a large number of synthetic problems, including ZDT, DTLZ, RE, MAF, WFG, Fi and UF problems.

1.2 Multiobjective Multitask Learning (MO-MTL) Problems

Method	$L_1$	$L_2$
Fairness classification	Binary cross entropy	DEO
Multiobjective classification	Cross entropy loss BR	Cross entropy loss UL
MO machine learning	Mean square loss	Mean square loss
MO distribution alignment	Similarity 1	Similarity 2

Notes:

DEO: Difference of Equality of Opportunity.

2. LibMOON Supported Solvers

LibMOON includes a variety of solvers tailored for different needs as image below shows.

2.1 Finite solution solvers

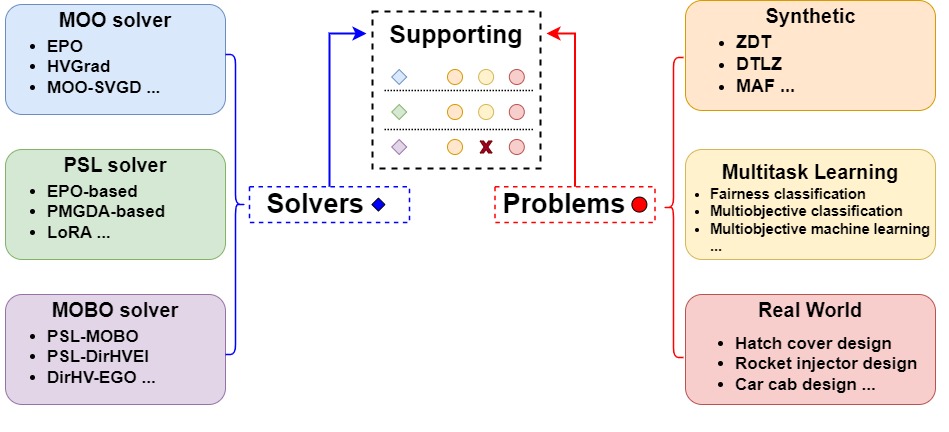
GradAggSolver
EPOSolver
MOO-SVGDSolver
MGDASolver
PMGDASolver
PMTLSolver
HVGradSolver

Method	Property	Paper	Complexity
EPO (Mahapatra et al 2020)	Exact solutions	paper	$O(m^2nK)$
MGDA-UB (Sener et al 2018)	Arbitrary solutions	paper	$O(m^2nK)$
PMGDA (Zhang et al 2024)	Specific solutions	paper	$O(m^2nK)$
Random (Lin et al 2021)	Arbitrary solutions	paper	$O(m^2nK)$
MOO-SVGD (Liu et al 2021)	Diverse solutions	paper	$O(m^2nK^2)$
PMTL (Lin et al 2019)	Sector solutions	paper	$O(m^2nK^2)$
HVGrad (Deist et al 2021)	Maximal HV solutions	paper	$O(m^2nK^2)$
Agg-LS (Miettinen et al 1999)	Convex hull solutions	book	$O(mnK)$
Agg-Tche (Zhang et al 2007)	Exact solutions	paper	$O(mnK)$
Agg-mTche (Ma et al 2017)	Exact solutions	paper	$O(mnK)$
Agg-PBI (Zhang et al 2007)	Approximate exact solutions	paper	$O(mnK)$
Agg-COSMOS (Ruchte et al 2007)	Approximate exact solutions	paper	$O(mnK)$
Agg-SoftTche (Lin et al 2024)	Fast approximate exact solutions	paper	$O(mnK)$

Notations:

$m$ is the number of objectives.
$K$ is the number of subproblems.
$n$ is the number of decision variables.

In neural network methods, $n$ is very large (>10,000), $K$ is also large (e.g., 20-50), and $m$ is relatively small (e.g., 2-4). Consequently, $m^2$ is not a significant issue, but $n^2$ and $K^2$ are major concerns.

2.2 Pareto set learning(PSL) Solvers

LibMOON supports various models of PSL solvers, categorized as follows:

Method	Property	Paper
EPO-based PSL (Navon et al 2021)	Exact solutions	paper
PMGDA-based PSL (Zhang et al 2024)	Specific solutions	paper
Aggregation-baed PSL (Sener et al 2018)	Minimal aggregation function solutions	paper
Evolutionary PSL (Sener et al 2018)	Mitigate local minimal by ES	paper
LoRA PSL (Chen et al 2024)	Light model structure	paper

2.3 MultiObjective Bayesian Optimization (MOBO) Solvers

PSL-MONO
PSL-DirHV-EI
DirHV-EGO

3. Installation and quick start

Libmoon is available on PyPI. You can install it using pip:

pip install libmoon==0.1.11

Example1: Finding a size-K (K=5) Pareto solutions with four lines of code.

from libmoon.solver.gradient.methods import EPOSolver
from libmoon.util.synthetic import synthetic_init
from libmoon.util.prefs import get_uniform_pref
from libmoon.util import get_problem

problem = get_problem(problem_name='ZDT1')
prefs = get_uniform_pref(n_prob=5, n_obj=problem.n_obj, clip_eps=1e-2)
solver = EPOSolver(step_size=1e-2, n_iter=1000, tol=1e-2, problem=problem, prefs=prefs)
res = solver.solve(x=synthetic_init(problem, prefs))

Example2: PSL in a problem with three lines of solving problem and two lines of evaluating the results.

from libmoon.solver.psl.core_psl import BasePSLSolver
from libmoon.util import get_problem
from libmoon.util.prefs import get_uniform_pref
from torch import Tensor

problem = get_problem(problem_name='ZDT1')
# agg list [ ’ls ’, ’tche ’, ’mtche ’, ’pbi ’, ... ]
prefs = get_uniform_pref(n_prob=100, n_obj=problem.n_obj, clip_eps=1e-2)
solver = BasePSLSolver(problem, solver_name='agg_ls')
model, _ = solver.solve()
eval_y = problem.evaluate(model(Tensor(prefs).cuda()))

4. Citing LibMOON and Acknowledgements

4.1 If you find our code useful, please cite our codebase:

@article{zhang2024libmoon,
      title={LibMOON: A Gradient-based MultiObjective OptimizatioN Library in PyTorch}, 
      author={Xiaoyuan Zhang and Liang Zhao and Yingying Yu and Xi Lin and Yifan Chen and Han Zhao and Qingfu Zhang},
      year={2024},
      journal={Advances in Neural Information Processing Systems},
}

4.2 Main Contributors

Name	Institution	Role
*Xiaoyuan Zhang ()**	CityUHK	Pareto set learning/MOO solvers/Project lead
*Liang Zhao ()**	CityUHK	MOBO
*Yingying Yu ()**	CityUHK	Software design
Xi Lin	CityUHK	Software design

(*): The first three authors contribute equally to this work.

4.3 Advisory Board

We sincernely thank the following contributors for their valuable contributions or feedbacks. We also want thanks for our collobrators from XDU, SZU, SUSTech, ECNU, NEU, SEU for their early use of our code.

We also espeically thank for the following contributors: Xuehai Pan, Hongzong Li, Zhe Zhao, Meitong Liu, Weiduo Liao, Baijiong Lin, Weiyu Chen, Prof. Jingda Deng, Prof. Yifan Chen, Prof. Ke Shang, Prof. Genghui Li, Prof. Han Zhao, Prof. Zhenkun Wang, Prof. Tao Qin, and Prof. Qingfu Zhang (Corresponding) .