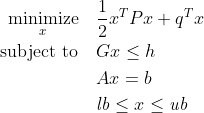QP Solvers for Python

Wrapper around Quadratic Programming (QP) solvers in Python, with a unified interface.

Installation

The simplest way to install this module is:

# Python 3
sudo apt install python3-dev
pip3 install qpsolvers

# Python 2
sudo apt install python-dev
pip2 install -r requirements2.txt

See also the documentation for other installation instructions.

Usage

The function solve_qp(P, q, G, h, A, b, lb, ub) is called with the solver keyword argument to select the backend solver. The convex quadratic program it solves is, in standard form:

Vector inequalities are taken coordinate by coordinate. The matrix P should be positive definite.

Example

To solve a quadratic program, simply build the matrices that define it and call the solve_qp function:

from numpy import array, dot
from qpsolvers import solve_qp

M = array([[1., 2., 0.], [-8., 3., 2.], [0., 1., 1.]])
P = dot(M.T, M)  # this is a positive definite matrix
q = dot(array([3., 2., 3.]), M).reshape((3,))
G = array([[1., 2., 1.], [2., 0., 1.], [-1., 2., -1.]])
h = array([3., 2., -2.]).reshape((3,))
A = array([1., 1., 1.])
b = array([1.])

x = solve_qp(P, q, G, h, A, b)
print("QP solution: x = {}".format(x))

This example outputs the solution [0.30769231, -0.69230769, 1.38461538].

Solvers

The list of supported solvers currently includes:

Dense solvers:
- CVXOPT
- qpOASES
- quadprog
Sparse solvers:
- ECOS
- Gurobi
- MOSEK
- OSQP

Frequently Asked Questions

Can I print the list of solvers available on my machine?
- Absolutely: print(qpsolvers.available_solvers)
Is it possible to solve a least squares rather than a quadratic program?
- Yes, qpsolvers also provides a solve_ls function.
I have a squared norm in my cost function, how can I apply a QP solver to my problem?
- You can cast squared norms to QP matrices and feed the result to solve_qp.
I have a non-convex quadratic program. Is there a solver I can use?
- Unfortunately most available QP solvers are designed for convex problems.
- If your cost matrix P is semi-definite rather than definite, try OSQP.
- If your problem has concave components, go for a nonlinear solver such as IPOPT e.g. using CasADi.
I get the following build error on Windows when running pip install qpsolvers.
- You will need to install the Visual C++ Build Tools to build all package dependencies.

Performances

On a dense problem, the performance of all solvers (as measured by IPython's %timeit on my machine) is:

Solver	Type	Time (ms)
quadprog	Dense	0.02
qpoases	Dense	0.03
osqp	Sparse	0.04
ecos	Sparse	0.34
cvxopt	Dense	0.46
gurobi	Sparse	0.84
cvxpy	Sparse	3.40
mosek	Sparse	7.17

On a sparse problem, these performances become:

Solver	Type	Time (ms)
osqp	Sparse	1
mosek	Sparse	17
ecos	Sparse	21
cvxopt	Dense	186
gurobi	Sparse	221
quadprog	Dense	550
cvxpy	Sparse	654
qpoases	Dense	2250

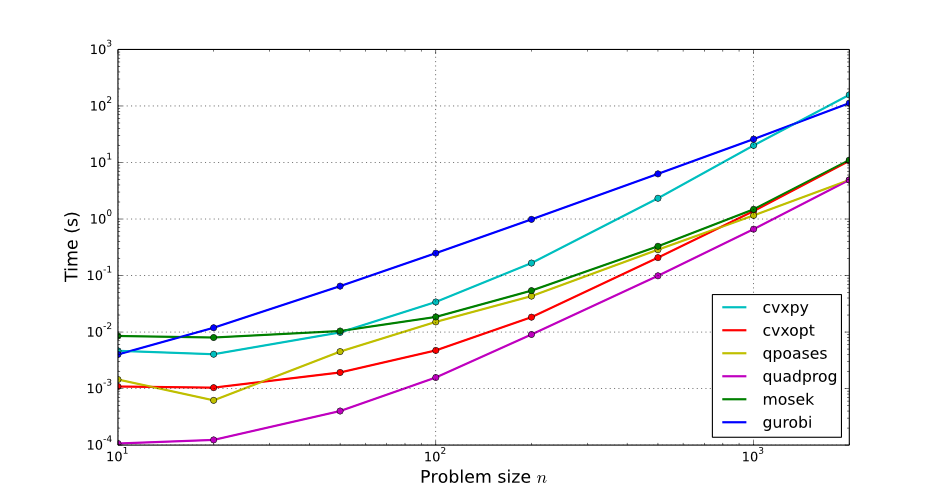
Finally, here are the results on a benchmark of random problems (each data point corresponds to an average over 10 runs):

Note that performances of QP solvers largely depend on the problem solved. For instance, MOSEK performs an automatic conversion to Second-Order Cone Programming (SOCP) which the documentation advises bypassing for better performance. Similarly, ECOS reformulates from QP to SOCP and works best on small problems.