/recurrent-slds

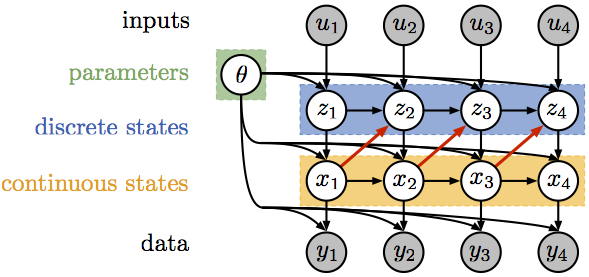
Recurrent Switching Linear Dynamical Systems

Primary LanguagePythonMIT LicenseMIT

recurrent-slds

Recurrent Switching Linear Dynamical Systems (rSLDS), like the standard SLDS they are based upon, are models for decomposing nonlinear time-series data into discrete segments with relatively simple dynamics. The recurrent SLDS introduces an additional dependency between the discrete and continuous latent states, allowing the discrete state probability to depend upon the previous continuous state. These dependencies are highlighted in red in the graphical model below.

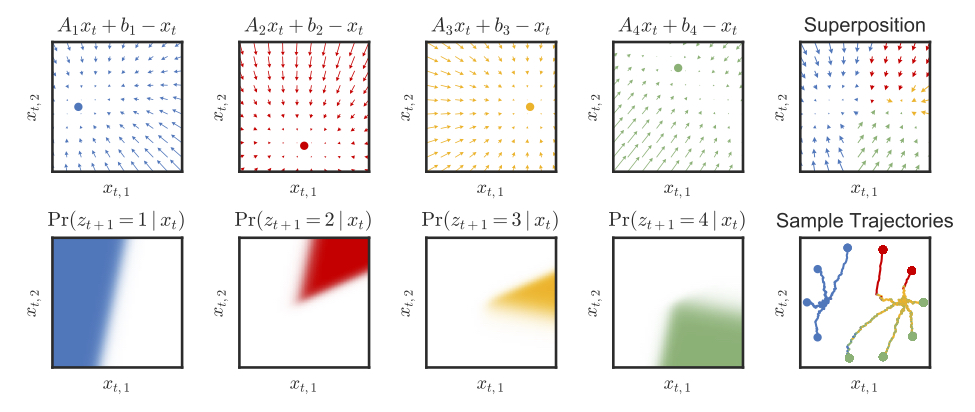
Probabilistic Model

These dependencies effectively cut up the continuous latent space into partitions with unique, linear dynamics. Composing these pieces gives rise to globally nonlinear dynamics. Here's an example of a 2D continuous latent state:

Probabilistic Model

In control literature, these models are known as hybrid systems. We develop efficient Bayesian inference algorithms for a class of recurrent SLDS. The important ingredient is an augmentation scheme to enable conjugate block Gibbs updates of the continuous latent states. Complete details of the algorithm are given in the following paper:

@inproceedings{linderman2017recurrent,
    title={Bayesian learning and inference in recurrent switching linear dynamical systems},
    author={Scott W. Linderman* and Johnson*, Matthew J. and Miller, Andrew C. and Adams, Ryan P. and Blei, David M. and Paninski, Liam},
    booktitle={Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS)},
    year={2017},
    link = {http://proceedings.mlr.press/v54/linderman17a/linderman17a.pdf},
}

Here's a link to the AISTATS paper.

Installation

This package is built upon many others, all of which are actively being developed. Follow the links to install these packages from source:

github.com/mattjj/pybasicbayes
github.com/mattjj/pyhsmm
github.com/mattjj/pylds
github.com/mattjj/pyslds
github.com/slinderman/pypolyagamma

Note that some of these have cython code which may need to be compiled. Follow the instructions on the project pages if you run into trouble.

Demo

Start with the NASCAR demo:

python examples/nascar.py

This will fit a recurrent switching linear dynamical system to synthetic NASCAR data, as in Figure 3 of the AISTATS paper.