My final year project using Microsoft SEAL. The purpose of this project is to Create Functionalities for Matrices and Vectors and Build a Logistic Regression model using Fully Homomorphic Encryption.
The code also contains some benchmark tests for matrix and vector operations as well as some examples based on the original examples already provided in the SEAL library.
Note: SEAL Version 3.4.5 is required. To view the graphs, you will need to have GNUPlot and Python 3 installed on your machine
- Setup for Linux
- Setup for Windows
- Matrix and Vector Operations
- Polynomial Evaluation
- Logistic Regression
- About the example files
- Bugs
First, make sure you have Microsoft SEAL installed. Follow the tutorial on https://github.com/Microsoft/SEAL.
If you have made any changes to the file name or added other files you will need to modify the CMakeLists.txt file accordingly.
To Build the project for the first time you need to run cmake . to generate the proper Makefile then you can build it with make.
Refer to the Windows installation of SEAL in https://github.com/Microsoft/SEAL.
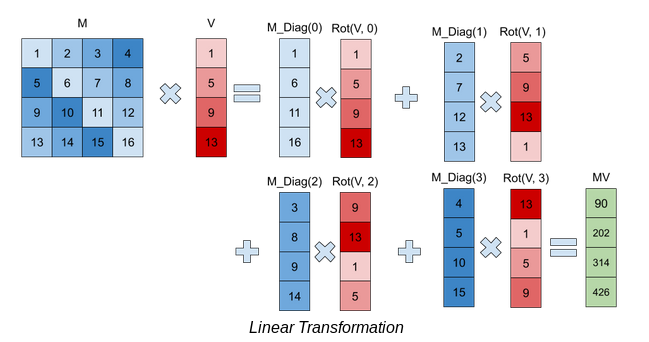
The linear_transformation.cpp file contains an implementation of the linear transformation algorithm in the paper: https://eprint.iacr.org/2018/1041.pdf .
This implementation uses rotations with element-wise multiplication and addition to perform matrix vector multiplication without using dot products. With the SIMD capability of SEAL, this method performs computations pretty quickly.
The linear_transformation2.cpp file is a similar to linear_transformation.cpp but without debugging statements and 3 test cases. You can use it to perform stress tests on certain parameters.
The drawing below shows an example of linear transformation with a 4x4 matrix:
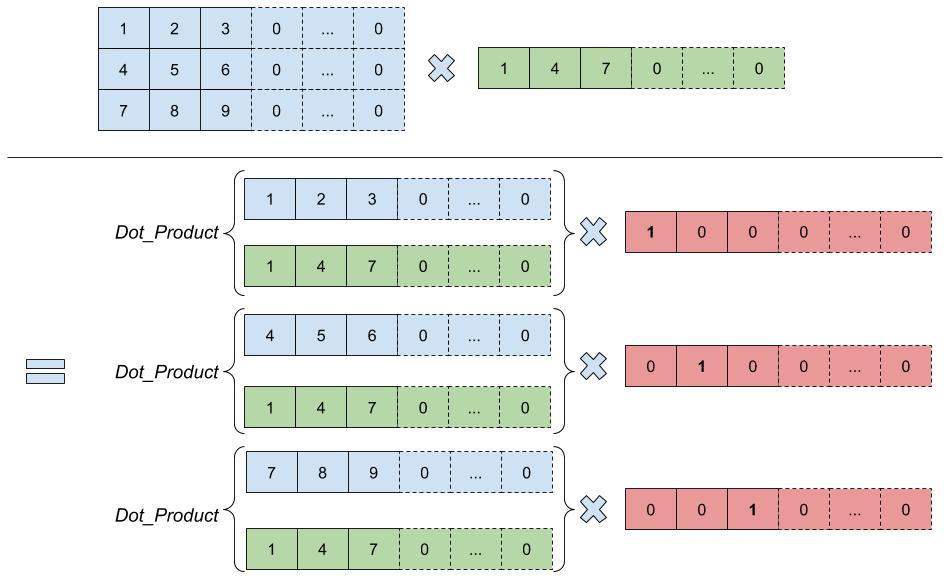
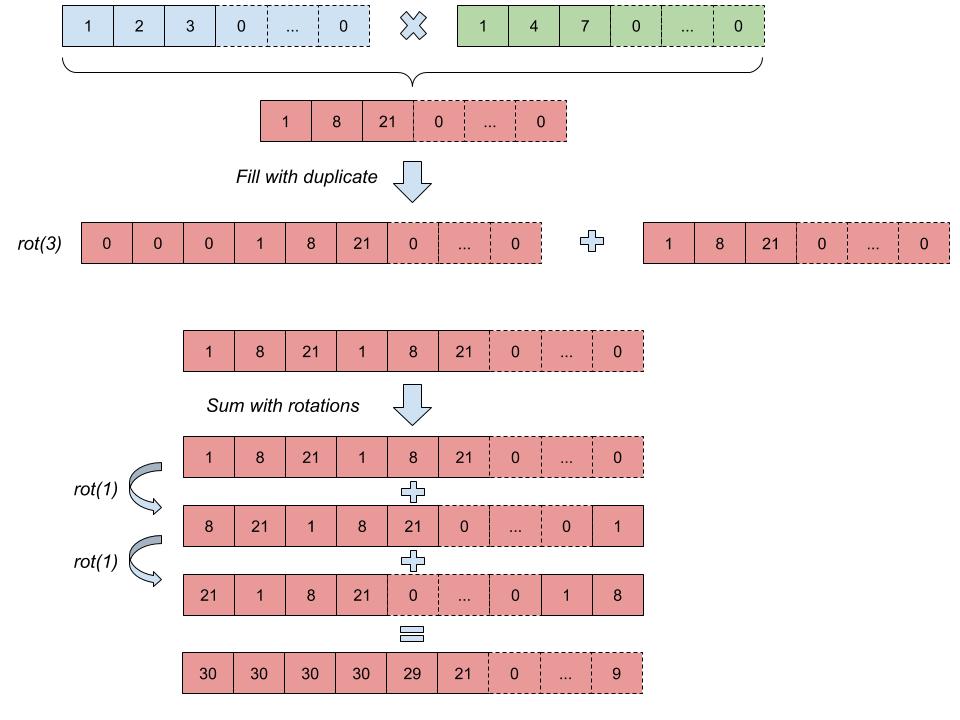
It is also possible to perform linear transformation on rectangular matrices using a hybrid approach proposed in in the paper “GAZELLE: A Low Latency Framework For Secure Neural Network Inference". However I have implemented another way of doing it illustrated below:
The dot products are computed as follows:
The matrix_multiplication.cpp file includes an implementation of the homomorphic matrix multiplication algorithm in the paper: https://eprint.iacr.org/2018/1041.pdf .
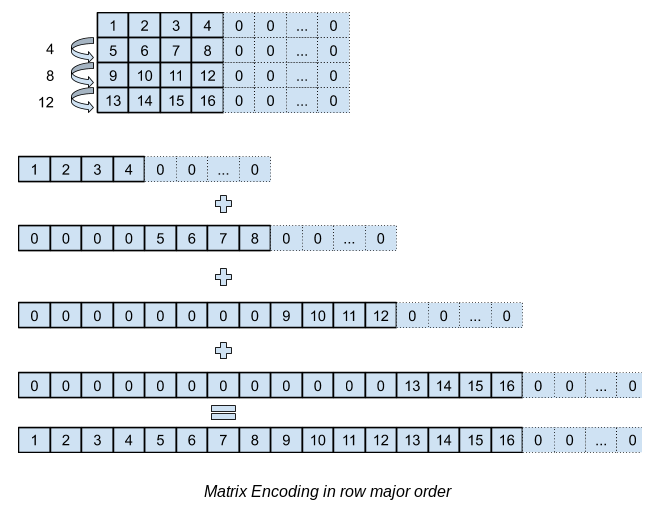
This implementation uses the linear transformation algorithm previously discusssed, Matrix Encoding and the 4 permutations of the input matrix: U_sigma, U_tau, V_k and W_k.
In order to compute those permutations, it is necessary to have the matrix encoded in row major order such as in this illustration:
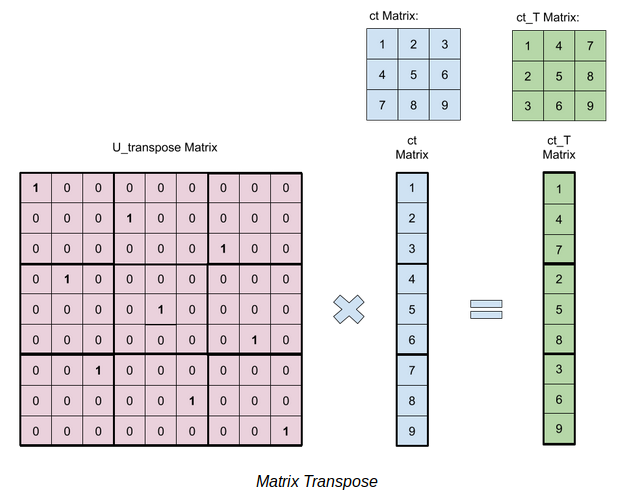
The matrix_transpose.cpp file contains method for homomorphically transposing a matrix. Since the tranpose of a matrix is technically a permuation, we can simply encode the matrix into a ciphertext vector and perform linear transformation with a matrix U_transpose with corresponding 1s and 0s. The illustration below shows an example of this method with a 3x3 matrix:
The matrix_ops.cpp file includes a naive method of performing matrix operations in CKKS. Here I am encoding every single element in the matrix and encrypting it instead of using entire rows from the matrix. A GNUPlot script and a data file are generated by running matrix_ops.
The vector_ops.cpp file consists of a small performance test for BFV and CKKS with poly_modulus_degree = 8192.
The benchmark.cpp file consists of performance tests for CKKS with 3 sets of input vectors of sizes 10, 100, 1000.
Running benchmark (after building the project) will generate a bench_<your poly modulus degree>.dat file and a corresponding script_<your poly modulus degree>.p file that can be used in GNUPlot. If you have gnuplot installed you can run the script file with gnuplot "script_<your poly modulus degree>". This will generate a canvas_"<your poly modulus degree>.html" with a graph of the output.
The benchmark2.cpp is similar to the first benchmark file.
The file polynomial.cpp contains 2 methods to evaluate polynomials using SEAL based on the works of Hao Chen in https://github.com/haochenuw/algorithms-in-SEAL/ :
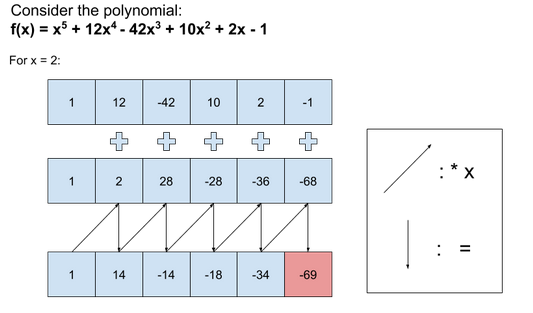
Horner's method for evaluating polynomials uses D multiplications and additions where D is the degree of the polynomial. Therefore the Modulus chain used must be of length greater than D+1 because of the rescaling and modulus switching operations required after every multiplication.
The drawing below shows an example of Horner's method:
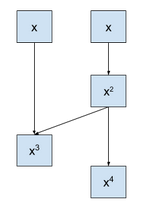
The tree method for evaluating polynomials uses log(D) multiplications and additions where D is the degree of the polynomial. This functions faster than Horner's method since it requires less operations which also allow us to have a lower poly_modulus_degree and smaller Modulus Chain.
The powers of x are pre-computed in a tree such as the example illustrated below:
The goal of this project is eventually to implement a logistic regression model that could work over encrypted data. The dataset used is pulsar_stars.csv simply because it was easy to use: the features are integers and the labels are at the last column 0s and 1s. To use this dataset properly the features matrix has to be standardized, that is why I built a standard_scaler function that performs (value - mean )/ standard_deviation over the values of the features matrix. I have also provided helper functions for transforming the CSV file into a matrix of floats. The code for logistic regression is based on the code and explanation in https://ml-cheatsheet.readthedocs.io/en/latest/logistic_regression.html .
This version of Logistic Regression has the functions:
sigmoid: returns the sigmoid of a valuepredict: returns the sigmoid of the linear transformation between the features and the weightscost_function: returns the costupdate_weightsor Gradient Descent: returns the updated weightstrain: returns the new weights and the cost history after a certain number of iterations of training
This version of Logistic Regression works on encrypted data using the CKKS scheme. It has the same functions as the normal logistic regression code except they have been modified to work using the SEAL functions. Since there is no way to write the sigmoid function 1/(1 + e^-value) in SEAL because there are no division and exponential operation in HE, an approximation of it is required. The polynomial approximation used here is based on the finding in the paper https://eprint.iacr.org/2018/074.pdf and is of the form:
f3(x) = 0.5 + 1.20096(x/8) - 0.81562(x/8)^3with a polynomial of degree 3f5(x) = 0.5 + 1.53048(x/8) - 2.3533056(x/8)^3 + 1.3511295(x/8)^5with a polynomial of degree 5f7(x) = 0.5 + 1.73496(x/8) - 4.19407(x/8)^3 + 5.43402(x/8)^5 - 2.50739(x/8)^7with a polynomial of degree 7
The polynomial approximation of the sigmoid function can be evaluated with the polynomial evaluation methods: Horner's and Tree method.
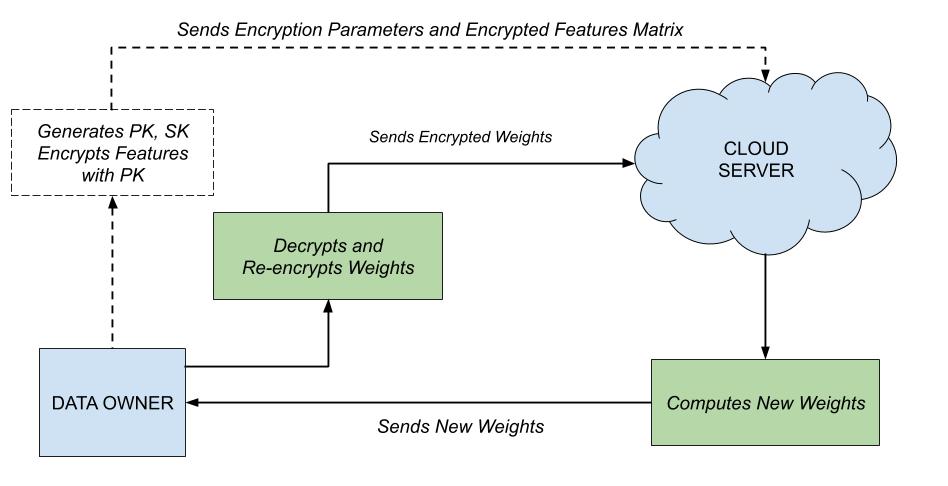
The protocol of the LR-CKKS works as follows:
In theory, using higher degree polynomials for approximating the sigmoid function is better however this would require a lot of rescaling which would lead to losing a lot of precision bits. In order to get the best precision and performance, I used the degree 3 polynomial with Horner's method.
All the explanations below are based on the comments and code from the SEAL examples. If you need a more detailed explaination, please refer to the original SEAL examples.
The first file is the 1_bfv.cpp. It contains an example on how to use the bfv scheme in SEAL. The BFV encryption scheme is used mainly to encrypt integers. It requires three parameters:
- Degree of Polynomial Modulus:
poly_modulus_degree - Ciphertext Coefficient Modulus:
coeff_modulus - Plaintext Coefficient Modulus:
plain_modulus
Each ciphertext has an invariant noise budget measured in bits that is consumed on every ciphertext operation. If the noise budget were to reach 0, the ciphertext would be too corrupted for decryption.
The noise budget is computed as follows: log2(coeff_modulus/plain_modulus). Choosing a larger coeff_modulus will give you a larger noise budget but will make computations a bit slower. The example provided uses a helper function from SEAL to create this parameter.
The size of a ciphertext in SEAL is the number of polynomials. A new ciphertext has a size of 2. Homomorphic Multiplication increases the size of the ciphertext: If two ciphertexts have sizes M and N then their multiplication will yield a size of M+N-1. The larger the ciphertext size the greater the consuption rate of the noise budget will be.
It is possible to reduce the size of ciphertexts from 3 to 2 by applying Relinearization to the ciphertexts. However this procedure comes at a certain computational cost.
There are 3 types of encoding that can be used in SEAL: Integer Encoding , Batch Encoding and CKKS Encoding.
The reason you may want to encode your Plaintext before encrypting it is to avoid integer overflow. Integer overflow happens when the plaintext coefficients exceed plain_modulus.
The modulus switching chain is a chain of other encryption parameters derived from the original parameters. The parameters in the modulus switching chain are the same as the original parameters with the exception that size of the coefficient modulus is decreasing going down the chain. The example provided shows a coeff_modulus of 5 primes of sizes {50, 30, 30, 50, 50} bits. Thus, there are 5 levels in this chain:
{50, 30, 30, 50, 50}-> Level 4 (Key level){50, 30, 30, 50}-> Level 3 (Data level){50, 30, 30}-> Level 2{50, 30}-> Level 1{50}-> Level 0 (Lowest level)
Modulus Switching is a technique of changing the ciphertext parameters down the chain. You may want to use this to gain computational performance from having smaller parameters. This method may reduce your ciphertext noise budget. If there is no need to perform further computations on a ciphertext, you can switch it down to the smallest (last) set of parameters in the chain before decrypting it.
The CKKS encryption scheme focuses on performing operations on encrypted real and complex numbers. Homomorphic multiplication in CKKS causes the scales in ciphertexts to grow. The scale can be considered as the bit precision of the encoding. The scale must not get too close to the total size of coeff_modulus. You can rescale to reduce the scale and stabilize the scale expansion. Rescaling is a type of modulus switching, it removes the last of the primes from the coeff_modulus but it scales down the ciphertext by the removed prime.
Suppose that the scale in a CKKS ciphertext is S and the last prime in the coeff_modulus is P. Rescaling to the next level changes the scale to S/P and removes the prime P from the coeff_modulus (just like in Modulus Switching). A good strategy is to set the initial scale S and primes P_i to be very close to each other. If ciphertexts have scale S before multiplication then they will have scale S^2 after multiplication and then S^2/P_i after rescaling thus S^2/P_i will be close to S again. Generally, for a circuit of depth D, we need to rescale D times, i.e., we need to be able to remove D primes from the coeff_modulus. Once we have only one prime left in the coeff_modulus, the remaining prime must be larger than S by a few bits to preserve the pre-decimal-point value of the plaintext.
Therefore a generally good strategy is to choose the parameters for the CKKS scheme as follows:
- Choose a
60 bitprime as as the first prime incoeff_modulusgiving us the highest precision when decrypting - Choose another
60 bitprime as the last prime incoeff_modulus - Choose the intermediate primes to be close to each other
The values I have used are {60, 40, 40, 60} with a poly_modulus_degree = 8192 which yields a coeff_modulus of 200 bits in total which is below max bit count for the poly_modulus_degree: CoeffModulus::MaxBitCount(8192) returns 218. The initial scale is set to 2^40. At the last level, this leaves us 60-40 = 20 bits of precision before the decimal point and around 10 to 20 bits of precision after the decimal point. Since our intermediate primes are 40 bits which is very close to 2^40 we are able to achieve stabilization as described earlier.
In the example, we're evaluating the polynomial PI*x^3 + 0.4x + 1. When computing x^2 (to compute x^3 later), you will notice that the scale will grow to 2^80. After rescaling the new scale should be close to 2^40 (NOT equal).
Rotation can be used in both BFV and CKKS schemes. It is a mechanism that allows you to rotate the encrypted vectors cyclically. It requires special keys called Galois keys which can be generated from the KeyGenerator class. It is possible to rotate the columns and rotate the rows. Rotations usually don't consume any noise budget. However, this is only the case when the special prime is at least as large as the other primes. The same applies for relinearization.
- Parameter mismatch CKKS LR ->
update_weights() - Ciphertext transparent in CKKS LR ->
update_weights()