This code tries to reproduce the 1989 Yann LeCun et al. paper: Backpropagation Applied to Handwritten Zip Code Recognition. To my knowledge this is the earliest real-world application of a neural net trained with backpropagation (now 33 years ago).
Since we don't have the exact dataset that was used in the paper, we take MNIST and randomly pick examples from it to generate an approximation of the dataset, which contains only 7291 training and 2007 testing digits, only of size 16x16 pixels (standard MNIST is 28x28).
$ python prepro.py
Now we can attempt to reproduce the paper. The original network trained for 3 days, but my (Apple Silicon M1) MacBook Air 33 years later chunks through it in about 90 seconds. (non-emulated arm64 but CPU only, I don't believe PyTorch and Apple M1 are best friends ever just yet, but anyway still about 3000X speedup). So now that we've run prepro we can run repro! (haha):
$ python repro.py
Running this prints (on the 23rd, final pass):
eval: split train. loss 4.073383e-03. error 0.62%. misses: 45
eval: split test . loss 2.838382e-02. error 4.09%. misses: 82
This is close but not quite the same as what the paper reports. To match the paper exactly we'd expect the following instead:
eval: split train. loss 2.5e-3. error 0.14%. misses: 10
eval: split test . loss 1.8e-2. error 5.00%. misses: 102
I expect that the majority of this discrepancy comes from the training dataset itself. We've only simulated the original dataset using what we have today 33 years later (MNIST). There are a number of other details that are not specified in the paper, so I also had to do some guessing (see notes below). For example, the specific sparse connectivity structure between layers H1 and H2 is not described, the paper just says that the inputs are "chosen according to a scheme that will not be dicussed here". Alternatively, the paper uses a "special version of Newton's algorithm that uses a positive, diagonal approximation of Hessian", but I only used simple SGD in this implementation because it is signficiantly simpler and, according to the paper, "this algorithm is not believed to bring a tremendous increase in learning speed". Anyway, we are getting numbers on similar orders of magnitude...
My notes from the paper:
- 7291 digits are used for training
- 2007 digits are used for testing
- each image is 16x16 pixels grayscale (not binary)
- images are scaled to range [-1, 1]
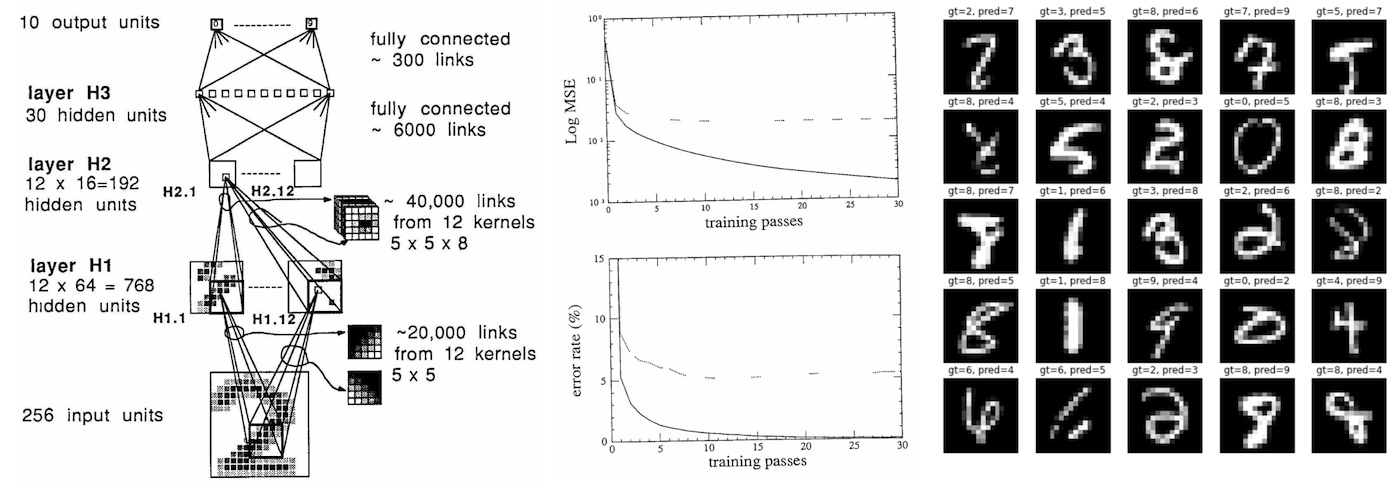
- network has three hidden layers H1 H2 H3
- H1 is 5x5 stride 2 conv with 12 planes. constant padding of -1.
- not "standard": units do not share biases! (including in the same feature plane)
- H1 has 768 units (8812), 19,968 connections (76826), 1,068 parameters (768 biases + 2512 weights)
- not "standard": H2 units all draw input from 5x5 stride 2 conv but each only connecting to different 8 out of the 12 planes
- H2 contains 192 units (4412), 38,592 connections (192 units * 201 input lines), 2,592 parameters (12 * 200 weights + 192 biases)
- H3 has 30 units fully connected to H2. So 5790 connections (30 * 192 + 30)
- output layer has 10 units fully connected to H3. So 310 weights (30 * 10 + 10)
- total: 1256 units, 64,660 connections, 9760 parameters
- tanh activations on all units (including output units!)
- weights of output chosen to be in quasi-linear regime
- cost function: mean squared error
- weight init: random values in U[-2.4/F, 2.4/F] where F is the fan-in. "tends to keep total inputs in operating range of sigmoid"
- training
- patterns presented in constant order
- SGD on single example at a time
- use special version of Newton's algorithm that uses a positive, diagonal approximation of Hessian
- trained for 23 passes over data, measuring train+test error after each pass. total 167,693 presentations (23 * 7291)
- final error: 2.5e-3 train, 1.8e-2 test
- percent misclassification: 0.14% on train (10 mistakes), 5.0% on test (102 mistakes).
- compute:
- run on SUN-4/260 workstation
- digital signal co-processor:
- 256 kbytes of local memory
- peak performance of 12.5M MAC/s on fp32 (ie 25MFLOPS)
- trained for 3 days
- throughput of 10-12 digits/s, "limited mainly by the normalization step"
- throughput of 30 digits/s on normalized digits
- "we have successfully applied backpropagation learning to a large, real-world task"
Open questions:
- The 12 -> 8 connections from H2 to H1 are not described in this paper... I will assume a sensible block structure connectivity
- Not clear what exactly is the "MSE loss". Was the scaling factor of 1/2 included to simplify the gradient calculation? Will assume no.
- What is the learning rate? I will run a sweep to determine the best one manually.
- Was any learning rate decay used? Not mentioned, I am assuming no.
- Was any weight decay used? not mentioned, assuming no.
- Is there a bug in the pdf where in weight init the fan in should have a square root? The pdf's formatting is a bit messed up. Assuming yes.
- The paper does not say, but what exactly are the targets? Assuming they are +1/-1 for pos/neg, as the output units have tanh too...
One more notes on the weight init conundrum. Eg the "Kaiming init" is:
a = gain * sqrt(3 / fan_in)
~U(-a, a)
For tanh neurons the recommended gain is 5/3. So therefore we would have a = sqrt(3) * 5 / 3 * sqrt(1 / fan_in) = 2.89 * sqrt(1 / fan_in), which is close to what the paper does (gain 2.4). So if the original work in fact did use a sqrt and the pdf is just formatted wrong, then the (modern) Kaiming init and the originally used init are pretty close.
- modernize the network using knowledge from 33 years of time travel.
- include my janky hyperparameter sweeping code for tuning the learning rate potentially