现将大部分原理从博客搬过来 详细的代码讲解和运行结果说明太长 还是请去我的博客查看:https://blog.csdn.net/weixin_43934607/article/details/100111813
这个百度比较多就不赘述了 在看到我的文章前一定也看了不少了!
开篇先说几点
- 本文是基于博客"https://blog.csdn.net/ironyoung/article/details/49455343"补充与拓展
- 本文努力去通俗的阐述bp神经网络原理 与结合实际bp网络图重构其代码 尤其核心算法部分 让bp算法使用更清晰明了 并且下面贴的代码注释非常全 也给出了用的哪个具体计算公式 很容易看懂
"d":输出值的正确结果 "o":实际输出值 "k":输出节点的个数(因为如果输出层节点不止一个时 就把多个节点的误差相加)
- 该式子是输出层误差的进一步分解
"f(netk)":是把输出层误差的"o"替换掉 "f(x)":指激活函数 本文用的"sigmoid"函数(激活函数通常不是自定 有固定的函数去选择) "netk":输入层从隐藏层取到 并且还没有经过激活函数的值
- 第二个式子使把"netk"又进一步分解 用隐藏层的值来表示
"j":隐藏层节点数(本文用的单层隐藏层) "w":隐藏层第j个节点对输出层第k个节点的加权 "y":第j个隐藏层节点的值(该值是已经经过了激活函数的值)
综上:输出层一个节点未经过激活函数的值"netk" 就等于(隐藏层每个节点的值 都乘其对输出层那个对应节点的加权)的和
- 该式子又是对隐藏层误差第二个式子的分解
"f(netj)":是把“yj"替换掉了("yj"指的隐藏层节点的值) 换成输入层的值来表示 "i":输入层的节点数 "v":输入层第i个节点对隐藏层第j个节点的加权 "x":输入层第i个节点输入的值
综上:隐藏层一个节点未经过激活函数的值"netk" 就等于(输入层每个节点输入的值 都乘其对隐藏层那个对应节点的加权)的和
总结:
- 实际上每次往前一层都是分解该层未经过激活函数的值 把该值用:(上一层每个节点的值*每个节点对该节点的加权)的和来替换 不断向前扩大 用前一层来替换
- 同时可以看到我们可以改变加权“w”、“v"来减小误差
"w7":一个隐藏层的一个加权 "net":输出层从隐藏层取到未经过加权的值 "out":经过加权函数后的值 "Eo1":o1节点的误差 "Etotal":所有节点最终的误差和
第一个偏导
第二个偏导
第三个偏导
综上所得各个偏导的乘积
"w1":输入层加权 "neth1":隐藏层获取输入层 且没经过激活函数的值 "outh1":经过激活函数的值 "neto1":输出层没加权的值 "outo1":输出层经过加权的值 也是最终输出结果 "Eo1":o1节点得误差 o2同理...
"outh1"为分叉处 所以用"Etotal"对"outh1"的偏导表示其之后所有的影响 下面又把对"outh1"的偏导进行拆分 分成两路
- 所以每次计算输入层偏导时要分成两部分来算
b1和b2指的是偏移(即:在加到下一层的时候 加权永远都是+1 但自己的值是改变的)
- 用o1的值举例偏移怎莫用
注意:b1的值对o1、o2是不同的值 一个节点有一个自己偏移值(输入层的节点都没有偏移值) 最后再加上该值就是未经过激活函数的net值
- 要修改偏移的话同理 用链式先画出影响的链 再一步一步偏导(下面的代码中有实现和讲解)
其他减小误差的方法就不赘述了 欢迎大佬补充
这个图就是我们一会儿要解决xor问题的神经网络图: 两个输入节点、一层隐藏层,且4个节点、一个输出节点
注意:
- 图中b1和b2指的是偏移 每个节点只有一个该值 用于从上一层获取到值之后加上该值 所以隐藏层每个节点都有其不同偏移b1、输出层每个节点也有其不同的偏移b2(输入层节点都没有偏移)
- net和out的区别是 net没经过激活函数但是已经加了偏移 out是net经过激活函数后的值 图中写成out形式 代表该节点的最终输出值
因为我们要用代码实现的神经网络图只有一个输出节点 所以这里的Etotal就是那一个输出节点的误差
1)依然用上面说的链式的原则 一直进行偏导 就得到上面的结果 2)最后"*1"是因为"neto1"对"b2"的偏导时 因为b2是偏移量 直接相加 所以偏移量对下一层的加权是1
这里以w9进行举例 其他加权做法相同
- 这里之所以用两个括号括起来 因为虽然咱们实现的bp网络只有一个输出节点 但是咱们在代码要遍历输出层的节点 遍历的时候咱们并不知道有多少个输出节点 所以用括号括起来
- 如果输出有多个节点 参照上面的"如何订正输入层加权" 把第一个括号里的式子进行拓展
- 最后对b1偏导的结果是1的道理跟上面相同
- 这里用w1进行举例 其他加权求变化量原理相同
- 用括号括起来也是因为代码中遍历输出节点时不知道节点个数 第一个式子会变成多个节点情况的和 但实际只有一个
- 通过上面可以看到,输出层节点偏移量的改变值和隐藏层加权的改变值只是最后一个偏导不同,隐藏层节点的偏移量和输入层节点加权的该变量也只是最后一个偏导的值不同
偏移更新的表达式同理
- 在正向传播获取值时:在遍历当前层节点时 遍历上一层节点(从隐藏层开始)
- 在反向传播获修改加权时:在遍历当前层节点时 遍历下一层节点 找到对应的加权
(该部分过长,包含了详细的代码注释还有运行运行训练结果说明,就不搬过来了,请去我的blog看吧!)
- 可以看出结果还是比较符合预期 在两个数相差很小时的判断结果就很接近0 其余情况就很接近1
- 在进行调整时 通过减少样本数提高误差的减小速度 从而可以输入更低的误差 但效果不是并很好 所以就选择增加样本 增大学习效率 同时输入一个折中的误差 似乎效果更好点
- 在设置训练数据的时候要尽量包含的范围段全一些 可以大幅提高准确率 但是训练数据如果设置的不太合理的话 可能会导致训练时误差减少的特别慢 最后训练次数可能达到最大值但也没到设置的误差阀值
- 在把误差从0.001降到0.0001之后 训练次数也是大幅翻倍甚至达到250w+次 但是准确率也明显提高 每组结果都更加接近0或1
如果有其他看法欢迎留言!!!



![[外链图片转存失败(img-uk0V5onh-1566937228531)(en-resource://database/1437:1)]](https://img-blog.csdnimg.cn/20190828042621146.png)
![[外链图片转存失败(img-OfVTK3Ig-1566937228532)(en-resource://database/1439:1)]](https://img-blog.csdnimg.cn/20190828042629458.png)
![[外链图片转存失败(img-pROmpG30-1566937228533)(en-resource://database/1435:1)]](https://img-blog.csdnimg.cn/20190828042640970.png)
![[外链图片转存失败(img-cZdonQYJ-1566937228534)(en-resource://database/1463:1)]](https://img-blog.csdnimg.cn/20190828042651923.png)
![[外链图片转存失败(img-JeG5NVlJ-1566937228535)(en-resource://database/1393:1)]](https://img-blog.csdnimg.cn/20190828042705716.png)
![[外链图片转存失败(img-6SW53z75-1566937228538)(en-resource://database/1367:1)]](https://img-blog.csdnimg.cn/20190828042727869.png)
![[外链图片转存失败(img-uqHdHe51-1566937228538)(en-resource://database/1375:1)]](https://img-blog.csdnimg.cn/20190828042735431.png)
![[外链图片转存失败(img-VM7lwo2H-1566937228539)(en-resource://database/1397:1)]](https://img-blog.csdnimg.cn/20190828042744313.png)
![[外链图片转存失败(img-3dfb1uPy-1566937228540)(en-resource://database/1403:1)]](https://img-blog.csdnimg.cn/20190828042751454.png)
![[外链图片转存失败(img-2uM1o9Kb-1566937228541)(en-resource://database/1405:1)]](https://img-blog.csdnimg.cn/20190828042758445.png)
![[外链图片转存失败(img-JOv1Ljeg-1566937228541)(en-resource://database/1457:1)]](https://img-blog.csdnimg.cn/20190828042815246.png)
![[外链图片转存失败(img-2Lu9Yipi-1566937228542)(en-resource://database/1445:1)]](https://img-blog.csdnimg.cn/20190828042842487.png)
![[外链图片转存失败(img-vfvqKQa6-1566937228543)(en-resource://database/1409:1)]](https://img-blog.csdnimg.cn/20190829161908860.png)
![[外链图片转存失败(img-dLR1nUAD-1566937228543)(en-resource://database/1449:1)]](https://img-blog.csdnimg.cn/20190828042858105.png)
![[外链图片转存失败(img-0MBNhMsN-1566937228544)(en-resource://database/1339:1)]](https://img-blog.csdnimg.cn/20190829162242605.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkzNDYwNw==,size_16,color_FFFFFF,t_70)
![[外链图片转存失败(img-hqu45bT3-1566937228545)(en-resource://database/1453:1)]](https://img-blog.csdnimg.cn/2019082804291924.png)
![[外链图片转存失败(img-nqICtA4j-1566937228545)(en-resource://database/1389:1)]](https://img-blog.csdnimg.cn/20190828042925680.png)
![[外链图片转存失败(img-n7q4NzBl-1566937228546)(en-resource://database/1431:1)]](https://img-blog.csdnimg.cn/20190828042935960.png)
![[外链图片转存失败(img-Y0t4dKVF-1566937228547)(en-resource://database/1433:1)]](https://img-blog.csdnimg.cn/20190828043007844.png)
![[外链图片转存失败(img-fgmnE2t0-1566937228547)(en-resource://database/1335:1)]](https://img-blog.csdnimg.cn/2019082804301955.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkzNDYwNw==,size_16,color_FFFFFF,t_70)
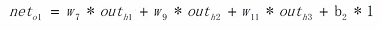

![[外链图片转存失败(img-kT3CO7OK-1566937228549)(en-resource://database/1539:1)]](https://img-blog.csdnimg.cn/20190828043036207.png)

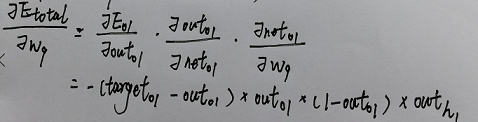
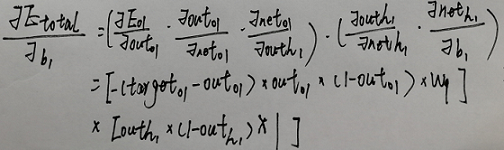
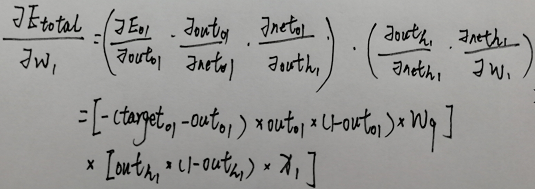
![[外链图片转存失败(img-m1PLAwk7-1566937228553)(en-resource://database/1551:1)]](https://img-blog.csdnimg.cn/20190828043114475.png)