/tsp_solving_dp_gvns

In this project we shall discuss on the Travelling Salesman Problem (TSP) and will take a few attempts to solve it, using Dynamic programming, or by using approximation algorithms (GVNS) and work on the corresponding python implementations.

Primary LanguageJupyter NotebookMIT LicenseMIT

Traveling Salesmen Problem Solving by Dynamic Programming & GVNS (TSP)

In this project we shall discuss on the Travelling Salesman Problem (TSP) a very famous NP-hard problem and will take a few attempts to solve it, using Dynamic programming, or by using approximation algorithms (GVNS) and work on the corresponding python implementations.

How to use the application ?

  1. Clone the project on your machine with :
    
git clone https://github.com/zakariamejdoul/tsp_solving_dp_gvns.git
  2. Run all cells in Jupyter Notebook file named main-app.ipynb.
  3. Put the instance path (you can use the instances provided in the folder named instances).
  4. Put your choice : 1 for dynamic programming method and 2 for GVNS metaheuristic method.
  5. Put your source city (the numbering order of cities starts with 1).
  6. If you have selected the choice 2 (GVNS method) you must provide the maximum execution time
    of the program in minutes.
  7. Enjoy the results !


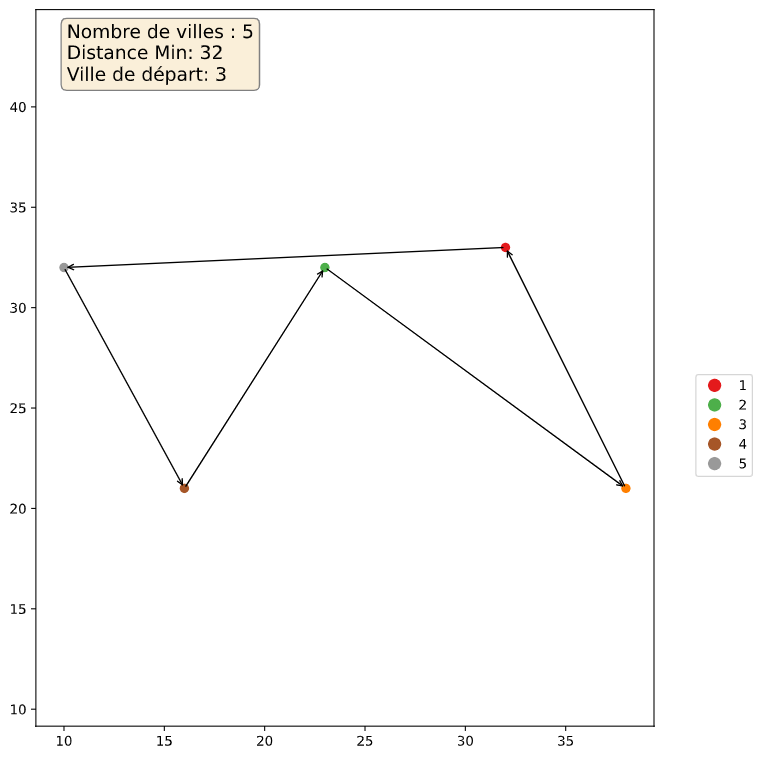
Results include the optimal path, the optimal distance and the target plot.


Your matrix : 

   0,   12,   10,   19,    8
  12,    0,    3,    7,    2
  10,    3,    0,    6,   20
  19,    7,    6,    0,    4
   8,    2,   20,    4,    0

TSP solver

******* Menu *******
Please choose one of these methods :
(1) Solve with dynamic programming 
(2) Solve with GVNS


OPTIMAL POLICY : [3, 1, 5, 4, 2, 3]
OPTIMAL VALUE : 32

Generated coordinates of cities : 
[[32 33]
 [23 32]
 [38 21]
 [16 21]
 [10 32]]

Plot Example