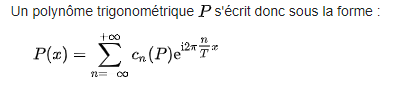Sur twitch, on essaie avec l'aide de quelques Viewers de synthétiser des sons avec du code !
Merci à MarcelPatulacci, j_l_22, bebertiii et tout/es les autres pour leur aide !
Vous pouvez retrouver :
- la vidéo sur ma chaîne youtube
- Le code, en libre accès, sur github. Vous pouvez même faire des pull Request et proposer vos modifs si vous le souhaitez ( et savez comment faire évidemment )
- l'application elle même, enfin du moins dans l'état où on l'a laissée à la fin du stream
- et dans ce document, que vous êtes en train de lire et pouvez retrouver ici quelques prises de notes théoriques ou remarques importantes faites pendant le stream !
Retrouvez plus d'infos sur mon twitter
Pour commencer , on a déjà juste essayé de jouer des sons "purs" à une fréquence donnée et il a fallut se demander quelle était la fréquence d'une note appelée "C" ou Do.
Il semblerait que la règle en vigueur chez nous, en occident,soit :
- on divise un octave en 12 demis ton
- le mi et le si n'ont pas de "#"
- du début à la fin d'une octave, on double de fréquence
- la fréquence de base, fondamentales, c'est le LA (A) à 440Hz pour des raisons arbitaires.
Avec ces 4 règles on peut construire l'ensemble de la gamme Tempérée à 12 tons avec du code !
Pour doubler de fréquence en 12 notes, ca veut dire que d'une note à la suivante on multiplie par 1.059 car :
C'est le principe "d'égale tempérament" ( apparemment. je l'apprend en meme temps que vous )
Du coup en terme de code ca donne ca :
const tunesName = [
"A",
"A#",
"B",
"C",
"C#",
"D",
"D#",
"E",
"F",
"F#",
"G",
"G#",
];
const A_STANDARD_PITCH = 440
const tuneValues = tunesName.map((note, idx) => ({
name: note,
freq: A_STANDARD_PITCH * 1.05946 ** idx,
}));qui nous fait :
[
{"name":"A","freq":440},
{"name":"A#","freq":466.16240000000005},
{"name":"B","freq":493.8804163040001},
{"name":"C","freq":523.2465458574359},
{"name":"C#","freq":554.3587854741191},
{"name":"D","freq":587.3209588584102},
{"name":"D#","freq":622.2430630721313},
{"name":"E","freq":659.2416356024004},
{"name":"F","freq":698.4401432553191},
{"name":"F#","freq":739.9693941732804},
{"name":"G","freq":783.9679743508237},
{"name":"G#","freq":830.5827101057238}
]Ce qui ne nous amène pas trop loin du G#5 théorique à 830.61Hz d'apres cette page..
Vous pouvez écouter le résultat ici
On peut constater en écoutant les notes que ca ne ressemble pas du tout à un instrument de musique réel et ça, apparemment serait du à une histoire d'harmonique.
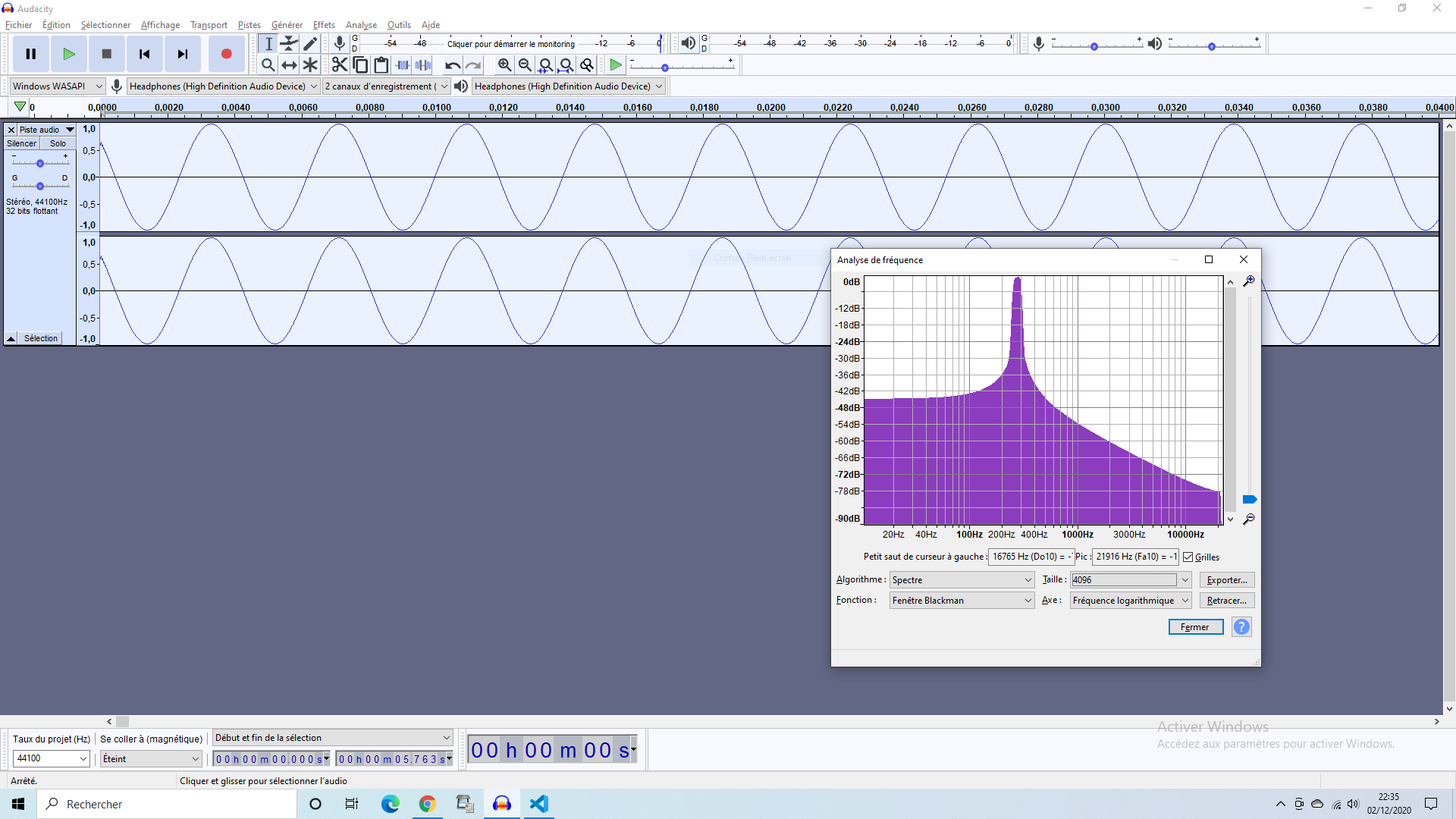
Voici la forme d'onde d'un DO ( C ) observé avec Audacity et sa "transformée de Fourier" ( son spectre fréquentiel )
Juste avant que le logiciel de Streaming ne plante !
Heureusement il existe dans l'API Web Audio une fonction "customWave" qui permet de définir ses propres formes d'ondes en décrivant les harmoniques.
L'API web Audio permet de produire une fonction d'onde personnalisée en fournissant la table des coefficients réels et imaginaires de la serie de Fourier de la fonction d'onde à produire.
Avec le Code suivant :
var oscillator = contexteAudio.createOscillator();
if (this.type === "custom") {
var real = new Float32Array(10);
var imag = new Float32Array(10);
real = [0, 0.8, 0.3, 0.5, 0.6, 0.4, 0.3, 0.5,0.4,0.6]
imag = [0, 0.8, 0.3, 0.5, 0.6, 0.4, 0.3, 0.5,0.4,0.6]
var wave = contexteAudio.createPeriodicWave(real, imag, {
disableNormalization: false,
});
// if you use your own periodic wave,
// do not set type
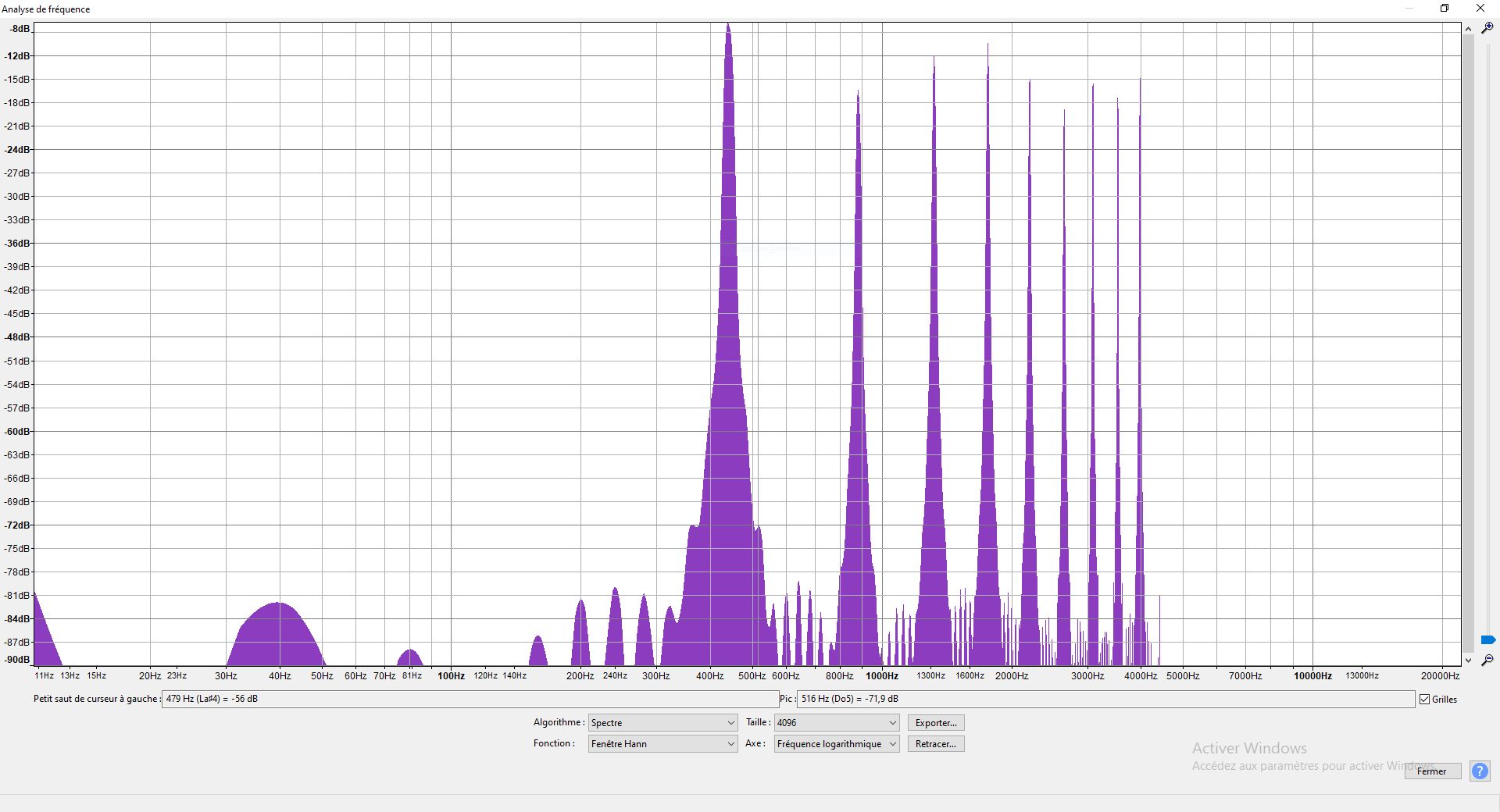
oscillator.setPeriodicWave(wave);On obtient le spectre suivant pour un LA à 440Hz :
( on voit des pics à 440HZ, puis 2 * 440 = 880 puis 3 * 440 = 1420Hz etc. Les petits pics sont dus aux sinus rajoutés par la partie imaginaire )
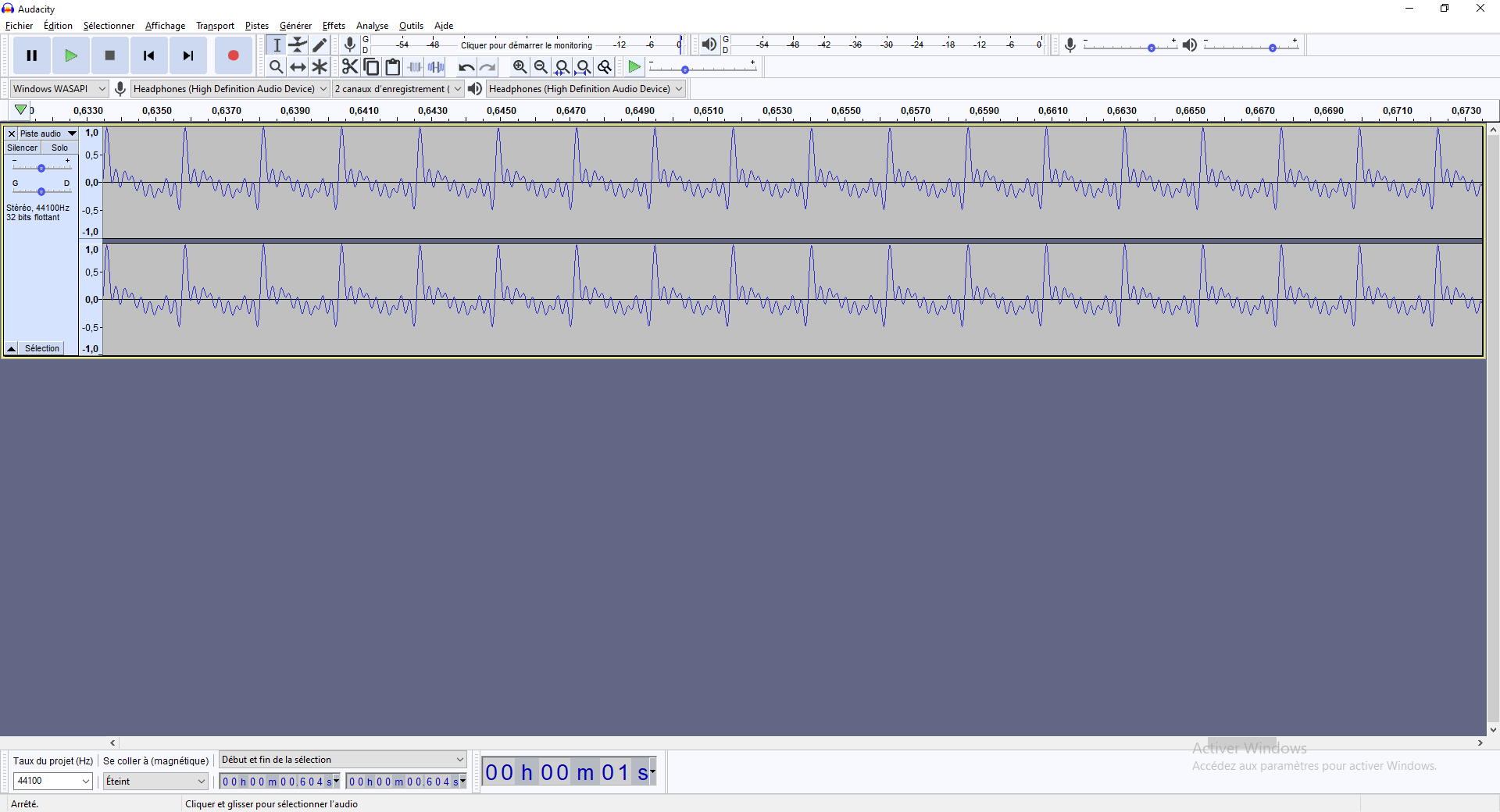
Ce spectre nous donne la fonction d'onde suivante :
Qui commence à ressembler à un son un peu plus naturel à l'oreille que la sinusoïde pure !
Cependant, on se sait pas exactement ce que sont ces "Coefficients de la série de Fourier"....
Cette formule là :
Se traduit ainsi en code :
def harmonique(freqFond, nth):
return np.cos(2*pi*time*nth*freqFondamental)
def generateHarmonic(freqFondamental, N):
h=np.zeros((N,len(time)))
for i in range(N):
h[i] = harmonique(freqFondamental,i+1)
return h
def sumHarmonics(f,N, coef):
H=generateHarmonic(f,N)
e=np.dot(coef,H)
return e
## N'importe quoi au hasard
c=np.array([1,0.4,0.8,0.1,0.3,0.6,0.2,0.1,0.1,0.05])
f=sumHarmonics(440,len(c), c)