Fast Fourier Transform Acceleration Algorithm. (Accelerated by CUDA)
基于FFT的蝶形公式,利用GPU的多核心优势,结合蝶形公式算法中同一层级的运算因子互不干扰的特点,对算法进行了并行化优化处理,加速效果十分显著。
在同一测试机器上,速度能达到Matlab(R2017b)的数十倍。
基于快速傅里叶变换的蝶形公式,对于N元待转换信号,蝶形公式为logN层级的子运算,每层的子运算中,运算因子在同层中互不干扰,因此只要利用好CUDA的__syncthreads()函数,在此基础上便可进一步利用GPU的单个线程来纵向处理每一个运算因子。
- 注意到蝶形公式中的旋转因子Wn^k大量重复出现,因此必须要对旋转因子做好预处理工作。由于预处理数据是静态的,故可考虑将其放入纹理单元以加速数据读取
- 使用
zero-copy(一种直接映射数据的技术)进行Host-Device之间的数据传输,减少数据传输成本 - 合理利用GPU的高速缓存等,尽量减少数据交换的通讯成本
- 算法上做一些合理优化,减少重复运算,同时及时释放空闲的内存占用,增加内存利用率
- GPU的sm单元间存在通信限制,因此要结合蝶形公式的算法结构,进一步改进算法以加强并行计算的性能
- Host到Device之间的内存数据传输仍然占用了大量时间,需要进一步改善数据传输的速度
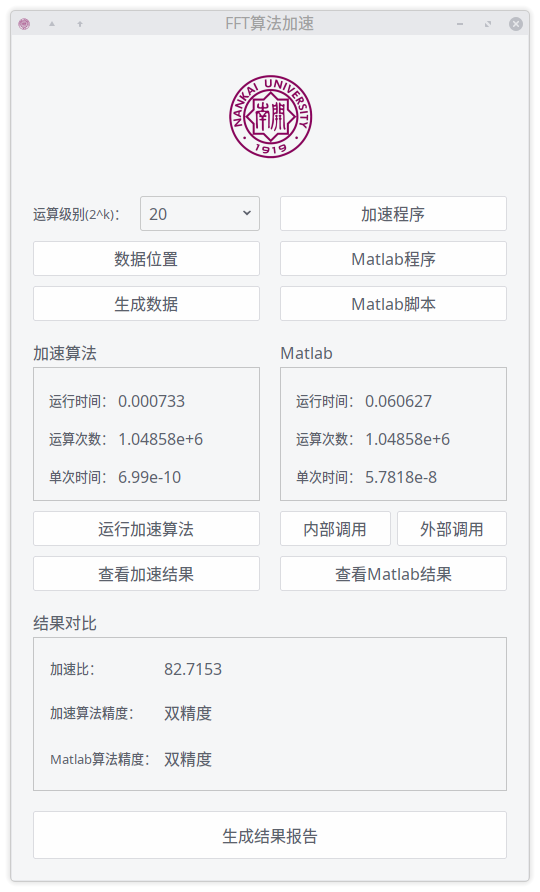
利用QT设计了简单的界面,具备一定的实用化功能