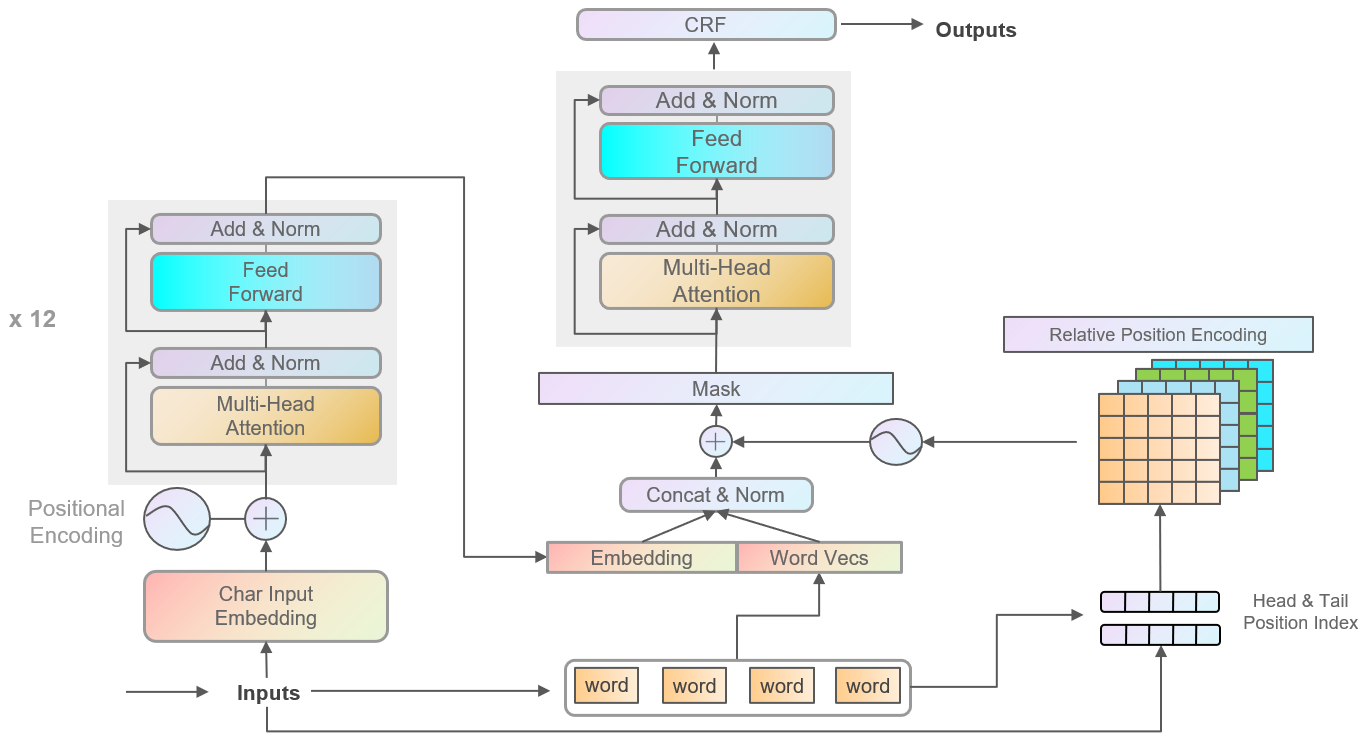
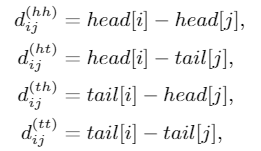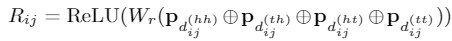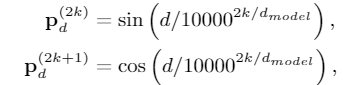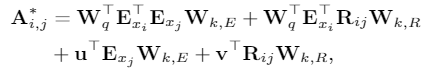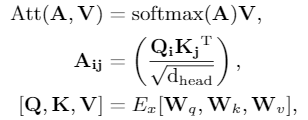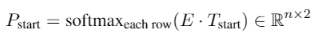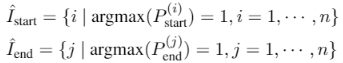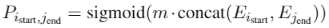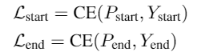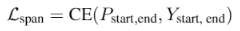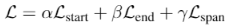模型结构上对结果影响较大的地方有：
- BERT 提取的特征和word embedding 组合时，需要对应 Head & Tail position，同时加一层 layer norm，收敛速度会加快。
- 由于是一层FLAT结构，FLAT的输出和输入的关联比较直接，需要将输入中pad的位置，mask为 0，效果会有一点提升。
另外可以试试Relative Position Encoding的不同融合方式。
PrivacyNER_with_NoisyData_CCF
|
├─ config.py
├─ preprocess.py
├─ main.py
├─ set_env.sh
├─ requirements.txt
├─ data
│ ├─ addition
│ ├─ dataset.py
│ └─ origin
├─ model
│ ├─ advTrain.py
│ ├─ layers
│ │ ├─ attention.py
│ │ ├─ encoder.py
│ │ ├─ flat.py
│ │ ├─ position.py
│ │ └─ structuredOut.py
│ ├─ model.py
│ ├─ mymodel.py
│ └─ trainer.py
├─ notebook
│ ├─ data_aug_nlpcda.ipynb
│ ├─ eda.ipynb
│ ├─ paddleNLP工具.ipynb
│ ├─ regex.ipynb
│ └─ traditional_model.ipynb
└─ utils
├─ callbacks
│ └─ earlystop.py
├─ postprocess
│ ├─ process.py
│ └─ selfsupervise.py
├─ preprocess
│ ├─ format.py
│ ├─ process.py
│ └─ tokenizer.py
└─ tools.py
FLAT部分Blog原文：https://mp.weixin.qq.com/s/6aU6ZDYPWPHc3KssuzArKw
论文：FLAT: Chinese NER Using Flat-Lattice Transformer
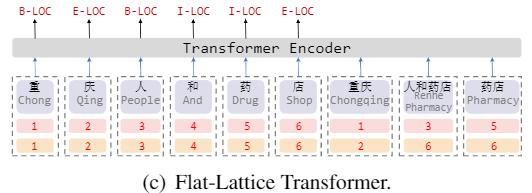
将Lattice图结构无损转换为扁平的Flat结构的方法，并将LSTM替换为了更先进的Transformer Encoder，更好地建模了序列的长期依赖关系；
提出了一种针对Flat结构的相对位置编码机制，使得字符与词汇信息交互更直接，在基于词典的中文NER模型中取得了SOTA。
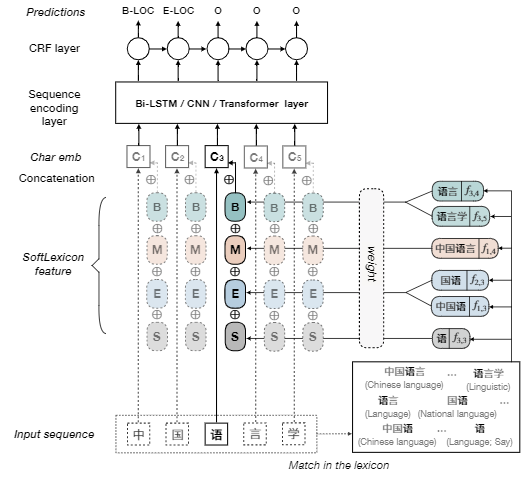
由于中文词汇的稀疏性和模糊性，基于字符的序列标注模型往往比基于词汇的序列标注模型表现更好，但在基于字符的模型中引入分词信息往往能够带来性能的提升，尤其是对于NER任务来说，词汇能够提供丰富的实体边界信息。
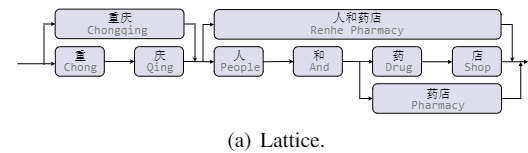
Lattice LSTM首次提出使用Lattice结构在NER任务中融入词汇信息，如图所示，一个句子的Lattice结构是一个有向无环图，每个节点是一个字或者一个词。
Lattice LSTM (ACL 2018): 将词汇信息引入中文NER的开篇之作，作者将词节点编码为向量，并在字节点以注意力的方式融合词向量。
Lexicon Rethink CNN(IJCAI 2019): 作者提出了含有rethink机制的CNN网络解决Lattice LSTM的词汇冲突问题。
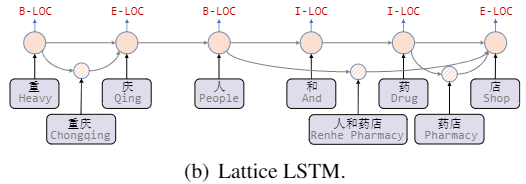
RNN和CNN难以建模长距离的依赖关系，且在Lattice LSTM中的字符只能获取前向信息，没有和词汇进行足够充分的全局交互
从Transformer的position representation得到启发，作者给每一个token/span(字、词)增加了两个位置编码，分别表示该span在sentence中开始(head)和结束(tail)的位置
扁平的结构允许我们使用Transformer Encoder，其中的self-attention机制允许任何字符和词汇进行直接的交互
span是字符和词汇的总称，span之间存在三种关系：交叉、包含、分离，然而作者没有直接编码这些位置关系，而是将其表示为一个稠密向量。作者用 和 表示span的头尾位置坐标，并从四个不同的角度来计算 和 的距离：
使用$A^{*}{i,j}$代替 tranformer 的self attention 中的 $A{i,j}$:
通过FLAT模型后，取出token的编码表示，将其送入CRF层进行解码得到预测的标签序列。
论文中给出的结果显示，FLAT相较于一众NER模型，取得了SOTA的效果。同时，使用较大规模数据时，效果更好。在对比实验中发现，字符与包含它的词汇之间的充分交互是很重要的。
class MultiHeadAttention(nn.Module):
def __init__(self, hidden_size, num_heads, scaled=True, attn_dropout=None):
super(MultiHeadAttentionRel, self).__init__()
self.hidden_size = hidden_size
self.num_heads = num_heads
self.per_head_size = self.hidden_size // self.num_heads
self.scaled = scaled
assert (self.per_head_size * self.num_heads == self.hidden_size)
# 正常 attention 的 q,k,v 变换矩阵
self.w_k = nn.Linear(self.hidden_size, self.hidden_size)
self.w_q = nn.Linear(self.hidden_size, self.hidden_size)
self.w_v = nn.Linear(self.hidden_size, self.hidden_size)
# 计算 Rij 的权重
self.w_r = nn.Linear(self.hidden_size, self.hidden_size)
# 计算 A* 的权重
self.u = nn.Parameter(torch.randn(self.num_heads, self.per_head_size), requires_grad=True)
self.v = nn.Parameter(torch.randn(self.num_heads, self.per_head_size), requires_grad=True)
self.dropout = nn.Dropout(attn_dropout)
def forward(self, key, query, value, pos, flat_mask):
"pos 为 自定义的 postion embedding，对应公式的 Rij"
batch = key.size(0)
# 输入线性变换
key = self.w_k(key)
query = self.w_q(query)
value = self.w_v(value)
rel_pos_embedding = self.w_r(pos)
####### 计算 A* 矩阵的方法 和 论文不是完全一致
# batch, seq_len, n_head, d_head
key = torch.reshape(key, [batch, -1, self.num_heads, self.per_head_size])
query = torch.reshape(query, [batch, -1, self.num_heads, self.per_head_size])
value = torch.reshape(value, [batch, -1, self.num_heads, self.per_head_size])
# batch, seq_len, seq_len, n_head, d_head
rel_pos_embedding = torch.reshape(rel_pos_embedding,
list(rel_pos_embedding.size()[:3]) + [self.num_heads, self.per_head_size])
# batch, n_head, seq_len, d_head
key = key.transpose(1, 2)
query = query.transpose(1, 2)
value = value.transpose(1, 2)
# batch, n_head, d_head, seq_len
key = key.transpose(-1, -2)
# 1, num_heads, 1, d_head
u_for_c = self.u.unsqueeze(0).unsqueeze(-2)
# batch, n_head, seq_len, d_head
query_and_u_for_c = query + u_for_c
# batch, n_head, seq_len, seq_len
A_C = torch.matmul(query_and_u_for_c, key)
# batch, n_head, seq_len, d_head, seq_len
rel_pos_embedding_for_b = rel_pos_embedding.permute(0, 3, 1, 4, 2)
# batch, n_head, seq_len, seq_len, 1, d_head
query_for_b = query.view([batch, self.num_heads, query.size(2), 1, self.per_head_size])
# batch, n_head, seq_len, seq_len, 1, d_head
query_for_b_and_v_for_d = query_for_b + self.v.view(1, self.num_heads, 1, 1, self.per_head_size)
# batch, n_head, seq_len, seq_len
B_D = torch.matmul(query_for_b_and_v_for_d, rel_pos_embedding_for_b).squeeze(-2)
# batch, n_head, seq_len, seq_len
attn_score_raw = A_C + B_D
# 计算 score
if self.scaled:
attn_score_raw = attn_score_raw / math.sqrt(self.per_head_size)
mask = 1 - flat_mask.long().unsqueeze(1).unsqueeze(1)
attn_score_raw_masked = attn_score_raw.masked_fill(mask.bool(), -1e15)
# batch, n_head, seq_len, seq_len
attn_score = F.softmax(attn_score_raw_masked, dim=-1)
attn_score = self.dropout(attn_score)
# batch, n_head, seq_len, d_head
value_weighted_sum = torch.matmul(attn_score, value)
# batch, seq_len, n_head, d_head -> batch, seq_len, hidden_size
result = value_weighted_sum.transpose(1, 2).contiguous().reshape(batch, -1, self.hidden_size)
return result教程博客很多，比如 http://jalammar.github.io/illustrated-bert/
参考 https://racleray.space/posts/798499bc.html, https://racleray.space/posts/6a1e61f5.html#%E5%91%BD%E5%90%8D%E5%AE%9E%E4%BD%93%E8%AF%86%E5%88%AB-1
论文：A Unified MRC Framework for Named Entity Recognition
转换为阅读理解（MRC）任务，来解决NER问题。似乎有很多搞研究的，都在尝试将NLP问题转换到MRC框架下，解决问题。
目的，解决NER中的实体重叠、嵌套关系问题。这是序列建模方式，比较难处理的问题。
数据，处理为三元组形式：(问题，答案，上下文)
其中，问题：一段对 实体类型 的描述文字，多种实体，就有多个问题；答案：为 实体的起始 index；上下文就是待识别的整个文本。
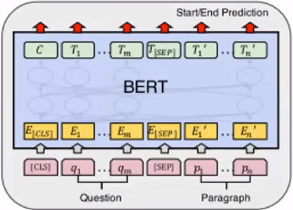
模型，使用BERT：
每个token预测输出有两个，是否为实体开始字，是否为实体结束字。
输出为 2 维，是和不是的预测概率。分别对每个位置判断，是否为开始字或者结束字。
但是这个两个集合，在有监督数据条件下，即训练时，并没有必要，只在预测推断时使用（推断需要通过下式计算所有组合的概率 P）。因为下式：
直接根据标注数据的 i, j 对标注部分计算 P。而不用对所有 i, j 组合算一次 P。
损失，多个预测损失之和：
权重为超参数。
论文：Simple-Lexicon：Simplify the Usage of Lexicon in Chinese NER
在Embedding信息的输入上进行改进，尝试了多种方式。
Softword：使用分词工具，标记词的 BMESO，结合字向量和标记向量输入。存在误差传播问题，无法引入一整个词汇对应word embedding
ExtendSoftword：组合所有字的所有BME，得到可能的词，但是无法复原原始的词汇信息是怎样
Soft-lexicon：对当前字符，依次获取BMES对应所有词汇集合。
根据词频加权词向量，与字向量求和。
该模型比Lattice LSTM, WC-LSTM等，在输入embedding上进行改进的模型，效果更好，更容易使用和迁移。
在只有正类和无标记数据的情况下，训练二分类器
Method 1 Directly
- 将正样本和部分筛选出的未标记样本分别看作是positive samples和negative samples
- 训练一个分类器，输出样本属于正、负类的概率
- 使用训练好的分类器。分类未标注数据，若正类的概率 大于 负类的概率，则该未标注样本的更可能为正类
Method 2 PU bagging
- 将所有正样本和未标记样本进行随机组合 bootstrap 来创建训练集；
- 将正样本和未标记样本视为positive和negative，训练一个分类器；
- 将分类器应用于不在训练集中的未标记样本 OOB（“out of bag”），并记录其分数；
- 重复上述三个步骤，最后每个未标记样本的分数为每一轮 OOB分数 的平均值。
Method 3
人工标注一部分确认为负类的数据，训练分类器识别这些 确认为 负类的数据。
论文：Distantly Supervised Named Entity Recognition using Positive-Unlabeled Learning，将PU Learning应用在NER任务上 Git Repo：
首先有 未标记数据 Du，实体字典 Dict；
使用最大匹配方法，标记一部分 Du，是NE则为正类，不是NE则为负类；
对每一种NE类型（比如，Loc，Nane）训练一个PU 分类器（自定义的神经网络模型）；
使用多个PU 分类器，对剩余的 Du，进行预测，每一个词，取预测概率最大的那一类标记；
若某些 词 多次被预测为 实体，且每次出现都被预测为同一类实体，那么，将这个词，加入Dict；
重复以上步骤，直到Dict不再改变。
方法是这么个方法，实际上代码并没有如此实现😅。代码里面的 loss mask 的使用方式，使用多个k flod 的子模型重新对训练数据进行预测投票，并删除得票数少于阈值的标记。目的是为了减少噪声数据。这和我查到的PU learning的**是不一致的。
另外，这种投票的方法可以用在 test data 中，但是是提取 得票数高于阈值的 样例和预测标记。加到训练数据中，如此这般 半监督学习，是不是更nice？嗯，想法不错。
对抗可以作为一种防御机制，并且经过简单的修改，便能用在NLP任务上，提高模型的泛化能力。对抗训练可以写成一个插件的形式，用几行代码就可以在训练中自由地调用。
在原始输入样本 上加一个扰动
，得到对抗样本后，用其进行训练。将输入样本向着损失上升的方向再进一步，得到的对抗样本就能造成更大的损失，提高模型的错误率。问题可以被抽象成这么一个模型：
其中， 为gold label，
为模型参数。Goodfellow认为，神经网络由于其线性的特点，很容易受到线性扰动的攻击。于是，他提出了 Fast Gradient Sign Method (FGSM) ：
其中， 为符号函数，
为损失函数。Goodfellow发现，令
，用这个扰动能给一个单层分类器造成99.9%的错误率。
Goodfellow还总结了对抗训练的两个作用：
- 提高模型应对恶意对抗样本时的鲁棒性；
- 作为一种regularization，减少overfitting，提高泛化能力。
从优化的视角，问题重新定义成了一个找鞍点的问题，Min-Max：内部损失函数的最大化，外部经验风险的最小化：
- 内部max是为了找到worst-case的扰动，也就是攻击，其中，
为损失函数，
为扰动的范围空间。
- 外部min是为了基于该攻击方式，找到最鲁棒的模型参数，也就是防御，其中
是输入样本的分布。
CV任务的输入是连续的RGB的值，而NLP问题中，输入是离散的单词序列，一般以one-hot vector的形式呈现，如果直接在raw text上进行扰动，那么扰动的大小和方向可能都没什么意义。Goodfellow在17年的ICLR中提出了可以在连续的embedding上做扰动。在CV任务，根据经验性的结论，对抗训练往往会使得模型在非对抗样本上的表现变差，然而神奇的是，在NLP任务中，模型的泛化能力反而变强了。
因此，在NLP任务中，对抗训练的角色不再是为了防御基于梯度的恶意攻击，反而更多的是作为一种regularization，提高模型的泛化能力。
对抗训练，FSGM的修改版本，取消了符号函数，对梯度计算进行scale，而不是只使用 +1 或者 -1 代替。
原网络进行一次，前向反向传播，得到梯度g
计算embedding矩阵的修正梯度 r:
$r=\frac{\epsilon g}{|g|_{2}}$ 输入 embedding + r ，计算对抗梯度 ga
将 ga 累加到 g 中，得到 gf
恢复原网络的embedding数值，使用 gf 对参数进行更新
Projected Gradient Descent（PGD）：“小步走，多走几步”，如果走出了扰动半径为 的空间，就映射回“球面”上，以保证扰动不要过大。
其中 为扰动的约束空间，
为小步的步长。
PGD模型能够得到一个非常低且集中的loss分布。
另外在半监督条件下，也可以使用对抗训练方法Virtual Adversarial Training进行半监督训练。
示例代码
import torch
grad_backup = {}
def save_grad(tensorName):
def backward_hook(grad: torch.Tensor):
grad_backup[tensorName] = grad
return backward_hook
class PGD:
def __init__(self, model):
self.model = model
self.emb_backup = {}
def attack(self,
epsilon=1.,
alpha=0.3,
emb_name='emb.',
is_first_attack=False):
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
if is_first_attack:
self.emb_backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = alpha * param.grad / norm
param.data.add_(r_at)
param.data = self.project(name, param.data, epsilon)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.emb_backup
param.data = self.emb_backup[name]
self.emb_backup = {}
def project(self, param_name, param_data, epsilon):
r = param_data - self.emb_backup[param_name]
if torch.norm(r) > epsilon:
r = epsilon * r / torch.norm(r)
return self.emb_backup[param_name] + r
def backup_grad(self):
# 此处也可以直接用一个成员变量储存 grad，而不用 register_hook 存储在全局变量中
for name, param in self.model.named_parameters():
if param.requires_grad:
param.register_hook(save_grad(name))
def restore_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
param.grad = grad_backup[name]
if __name__ == '__main__':
# 示例过程
pgd = PGD(model)
K = 3 # 小步走的步数
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播，得到正常的grad
pgd.backup_grad()
# 对抗训练
for t in range(K):
pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
if t != K-1:
model.zero_grad()
else:
pgd.restore_grad()
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播，并在正常的grad基础上，累加对抗训练的梯度
pgd.restore() # 恢复embedding参数
# 梯度下降，更新参数
optimizer.step()
model.zero_grad()import torch
class FGM:
def __init__(self, model):
self.model = model
self.backup = {}
def attack(self, epsilon=1, emb_name='emb.'):
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_adv = epsilon * param.grad / norm
param.data.add_(r_adv)
def restore(self, emb_name='emb.'):
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
if __name__ == "__main__":
# 示例过程
fgm = FGM(model)
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播，得到正常的grad
# 对抗训练
fgm.attack() # 在embedding上添加对抗扰动
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播，并在正常的grad基础上，累加对抗训练的梯度
fgm.restore() # 恢复embedding参数
# 梯度下降，更新参数
optimizer.step()
model.zero_grad()Stochastic Weight Averaging，方法的提出者认为，训练期间得到的局部最小值 倾向于 在损失值较低的区域的边界，而不是集中在损失更低的区域中心部分。所以，Stochastic Weight Averaging可以通过对边界的平均，得到更好性能和更好泛化性能的模型。Git Repo
保存两套权重w, wswa；
使用循环学习率，训练w；
达到指定轮次，更新ws，$n_{models}$指更新$w_{swa}$时，中间间隔的轮次:
$w_{swa} = \frac{w_{swa}n_{models}+w}{n_{models}+1}$ 循环以上步骤，最后使用wswa，作为最终模型
有可以直接使用的工具，比较方便。from torchcontrib.optim import SWA
optimizer = torch.optim.Adam(params_lr)
# Stochastic Weight Averaging
optimizer = SWA(optimizer)
if ...:
optimizer.update_swa()
...
# 训练结束时使用收集到的swa moving average
optimizer.swap_swa_sgd()
# optimizer.bn_update(
# train_dataloader,
# model) # 更新BatchNorm的 running mean
# save参考链接：