zergnick/hilbert_curve

maps between 1-D space filling hilbert curve and N-D coordinates

Introduction

This is a module to convert between one dimensional distance along a Hilbert curve, h, and N-dimensional coordinates, (x_0, x_1, ... x_N-1). The two important parameters are N (the number of dimensions, must be > 0) and p (the number of iterations used in constructing the Hilbert curve, must be > 0).

We consider an N-dimensional hypercube of side length 2^p. This hypercube contains 2^{N p} unit hypercubes (2^p along each dimension). The number of unit hypercubes determine the possible discrete distances along the Hilbert curve (indexed from 0 to 2^{N p} - 1). The image below illustrates the situation for N=2 and p=3.

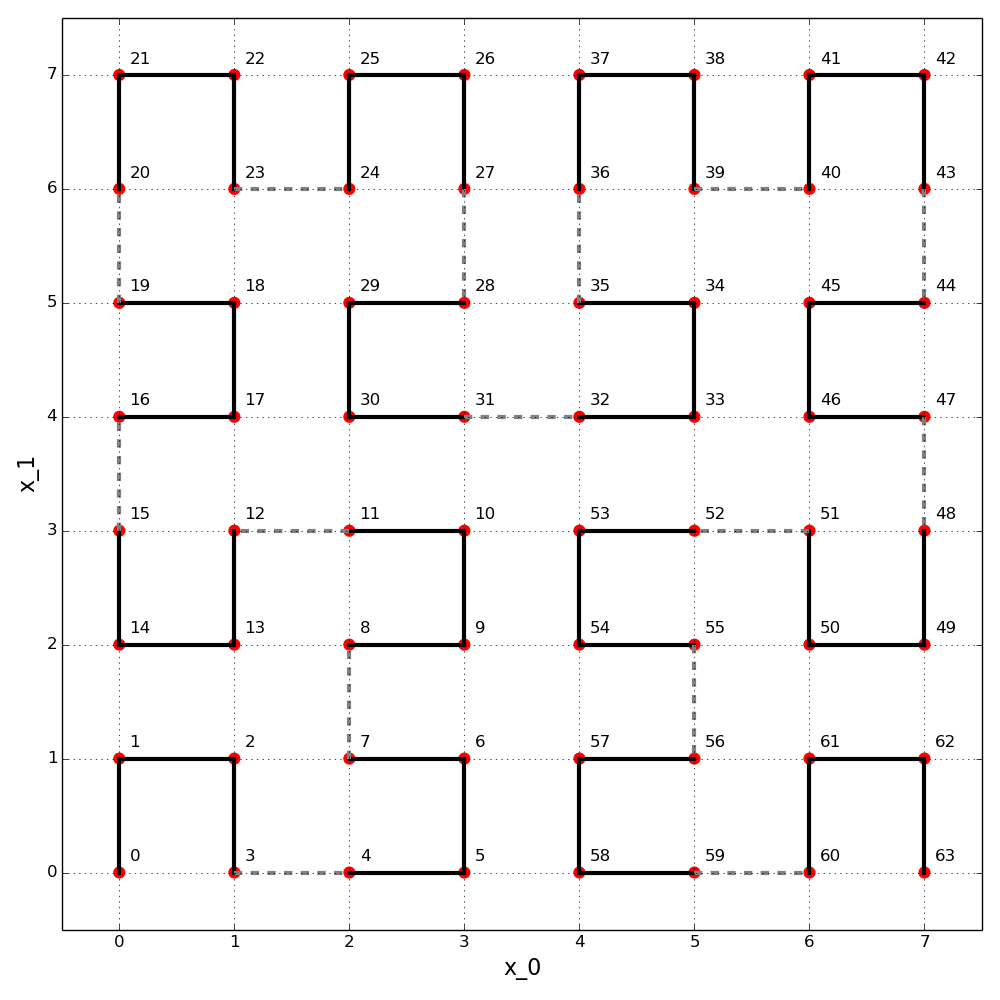
This is the third iteration (p=3) of the Hilbert curve in two (N=2) dimensions. Distances, h, along the curve are labeled from 0 to 63 (i.e. from 0 to 2^{N p}-1). The provided functions translate between N-dimensional coordinates and the one dimensional distance. For example, between (x_0=4, x_1=6) and h=36.

Reference

This module is based on the C code provided in the 2004 article "Programming the Hilbert Curve" by John Skilling,

• http://adsabs.harvard.edu/abs/2004AIPC..707..381S

I was also helped by the discussion in the following stackoverflow post,

• mapping-n-dimensional-value-to-a-point-on-hilbert-curve

which points out a typo in the source code of the paper. The Skilling code provides two functions TransposetoAxes and AxestoTranspose. In this case, Transpose refers to a specific packing of the integer that represents distance along the Hilbert curve (see below for details) and Axes refer to the N-dimensional coordinates. Below is an excerpt of the docs from that code that appears in the paper by Skilling,

//+++++++++++++++++++++++++++ PUBLIC-DOMAIN SOFTWARE ++++++++++++++++++++++++++
// Functions: TransposetoAxes  AxestoTranspose
// Purpose:   Transform in-place between Hilbert transpose and geometrical axes
// Example:   b=5 bits for each of n=3 coordinates.
//            15-bit Hilbert integer = A B C D E F G H I J K L M N O is stored
//            as its Transpose
//                   X[0] = A D G J M                X[2]|
//                   X[1] = B E H K N    <------->       | /X[1]
//                   X[2] = C F I L O               axes |/
//                          high  low                    0------ X[0]
//            Axes are stored conveniently as b-bit integers.
// Author:    John Skilling  20 Apr 2001 to 11 Oct 2003