Project

GP-DRT: Gaussian Process Distribution of Relaxation Times

This repository contains some of the source code used for the paper entitled "The Gaussian Process Distribution of Relaxation Times: A Machine Learning Tool for the Analysis and Prediction of Electrochemical Impedance Spectroscopy Data" https://doi.org/10.1016/j.electacta.2019.135316, the preprint is also available in the docs folder.

Introduction

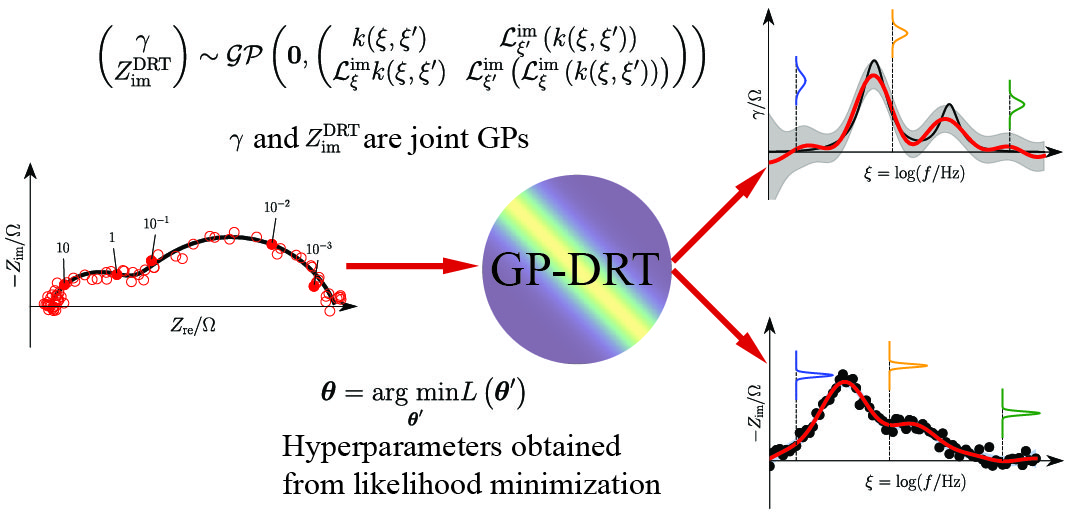
The distribution of relaxation times (DRT) [1] is an elegant approach for the analysis of electrochemical impedance spectroscopy (EIS) data encountered in materials science, electrochemistry, and other fields. However, deconvolving the DRT from EIS data is an ill-posed problem [2-3], which is particularly sensitive to experimental errors. Several well-known approaches [2-5] can overcome this issue, but they all require the use of ad hoc hyperparameters. Furthermore, most methods are not probabilistic and therefore, do not provide any insight into uncertainty regarding the estimated DRT. GP-DRT [6] is our newly developed approach that can obtain both the DRT mean and covariance from the EIS data. It can also predict the DRT and the imaginary part of the impedance at frequencies that were not previously measured. One crucial point of the GP-DRT method is that the parameters that define the GP-DRT model can be selected rationally by maximizing the experimental evidence. The GP-DRT approach was tested against both synthetic experiments and “real” experiments. We found that the GP-DRT can manage considerable noise, overlapping timescales, truncated data, and inductive features.

Figure 1. Schematic illustration of the GP-DRT method.

Dependencies

numpy

scipy

matplotlib

pandas

Tutorials

ex1_single_ZARC.ipynb: this notebook shows how one can recover the DRT from impedance synthesized using a single ZARC element consisting of a resistance placed in parallel to a constant phase element (CPE). The frequency range is from 1E-4 Hz to 1E4 Hz with 10 points per decade (ppd).
ex2_double_ZARC.ipynb: this notebook shows how the GP-DRT model can manage overlapping timescales from two ZARC elements in series. The frequency range is from 1E-4 Hz to 1E4 Hz with 10 ppd.
ex3_truncated_ZARC.ipynb: this notebook shows how the GP-DRT model can

recover the DRT from atruncated EIS spectrum (data points at lower frequencies, i.e., f < 1E-3 Hz, are not available), and
predict the impedance value at these frequencies.

ex4_experiment.ipynb: shows an example using experimental EIS data. In this tutorial, the EIS data is read from acsv file and the DRT is predicted by the GP-DRT model.
ex5_inductance_plus_ZARC.ipynb: this notebook adds an inductance to the model used in ex1_single_ZARC.ipynb

Citation

@article{liu2019gaussian,
  title={The Gaussian process distribution of relaxation times: A machine learning tool for the analysis and prediction of electrochemical impedance spectroscopy data},
  author={Liu, Jiapeng and Ciucci, Francesco},
  journal={Electrochimica Acta},
  pages={135316},
  year={2019},
  publisher={Elsevier}
}

References