doubletree:
An R package for Empowering Domain-Adaptive Probabilistic Cause-of-Death Assignment using Verbal Autopsy via Double-Tree Shrinkage
Maintainer: Zhenke Wu, zhenkewu@umich.edu
References: If you are using doubletree for tree-informed Bayesian domain adaptation, please cite the following preprint:
| Citation | Paper Link | |
|---|---|---|
| 1. | Wu Z, Li RZ, Chen I, Li M (2023+). Tree-informed Bayesian multi-source domain adaptation: cross-population probabilistic cause-of-death assignment using verbal autopsy. | Arxiv |
# install bioconductor package `ggtree` for visualizing results:
devtools::install_github("https://github.com/YuLab-SMU/ggtree")
install.packages("devtools",repos="https://cloud.r-project.org")
devtools::install_github("zhenkewu/doubletree")Ascertaining the causes of deaths absent vital registries presents a major barrier to under-standing cause-specific burdens of mortality and public health management. Verbal autopsy(VA) surveys are increasingly adopted in these resource poor settings. Relatives of a deceased person are interviewed about symptoms leading up to the death. Statistical methods have been devised for estimating the cause-specific mortality fractions (CSMF). However, expansion of VA from established to new sites has raised acute needs of domain-adaptive and accurate CSMF estimation methods that can handle imbalanced and sparse death counts in many cause-domain combinations. In this paper, we propose a method that starts with a hierarchy for the domains and adaptively learns the between-domain similarity in the conditional distribution of the survey responses given a cause. In addition, the method uses a second pre-specified cause hierarchy to borrow information across cause groups so that each group has similar conditional response probabilities. Through simulation studies, the method, referred to as “double-tree shrinkage”,is shown to improve the precision and reduce the asymptotic bias in estimating CSMFs as a result of the flexible and adaptive conditional dependence structure estimation. We also evaluate and illustrate the method using PHMRC VA data. The paper concludes with a discussion on limitations, extensions and highlights the central role of domain adaptivity offered by the proposed method in ongoing VA survey research.
The doubletree package works with the following scenarios:
-
Scenario a: No missing leaf labels in tree1 or tree2, for all observations; So this is reduced to a nested latent class model estimation prorblem with parameter shrinkage according to the two trees.
-
Scenario b: All missing tree1 leaf label occurred for in a single leaf node in tree2 (say v2):
- Scenario b1: No observation with observed tree1 label in leaf v2;
- Scenario b2: More than 1 observations have observed tree1 label in leaf v2.
-
Scenario c: Missing tree1 leaf labels occurred for observations in 2 or more leaf nodes in tree2, say the leaf node set S:
- Sub-scenarios: 0,1,2,... leaf/leaves in S have partially observed leaf label in tree1
-
main function
nlcm_doubletree -
A simple workflow using simulated data and two trees obtained from PHMRC data; also check out the
openVApackage that processed the raw data into binary indicators: openVA.- in
R, check the example byexample(nlcm_doubletree); note that this example uses the hierarchies, but simulates data based on a set of true parameters and sample sizes. - Trajectory of the lower bound of ELBO
- in
-
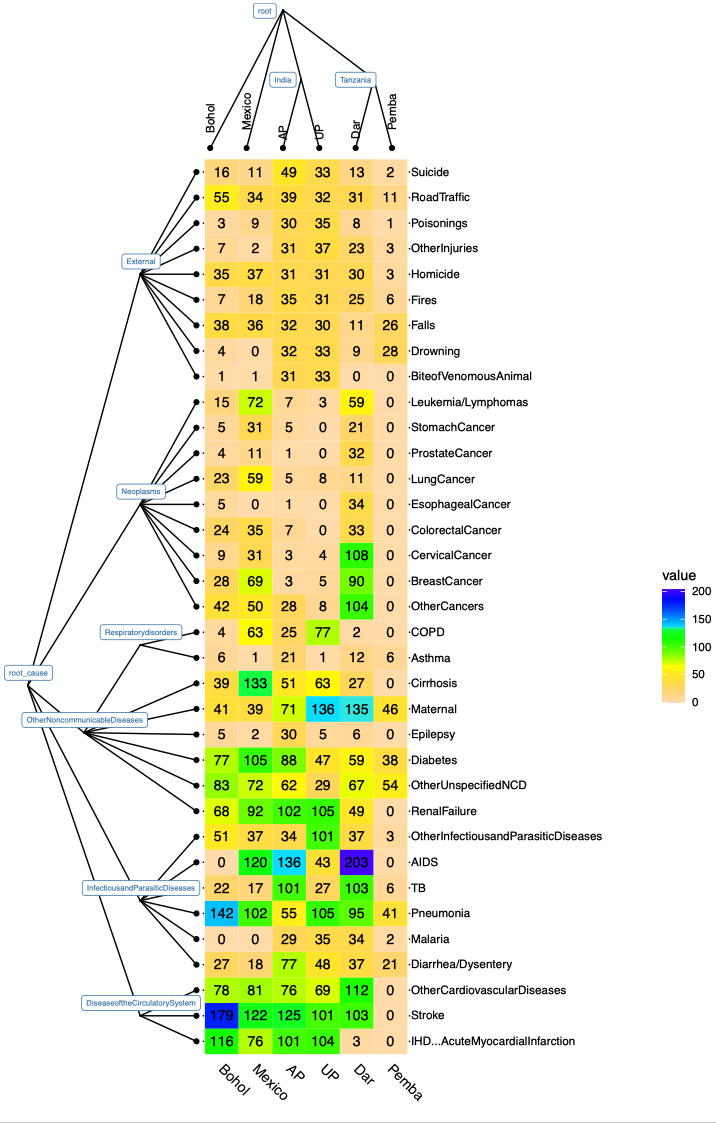
the hierarchy for 35 causes and the hierarchy for 6 domains is shown below. The numbers in the cells indicate the number of physician-coded cause-of-death (COD) in a particular site ("domain"). In the most common situation this package is designed for, we would not observe the membership of some deaths to the cells. For example, in
APsite, we may not be able to see the tabulation by the CODs (by row), but just a total number of deaths inAP(the column sum for AP in the table shown here).doubletreewill provide an estimate of- the population cause-specific mortality fraction in
AP(a vector of length 35 that sums to 1); - individual-specific posterior probability of CODs (a vector of length 35 that sums to 1), based on which we may obtain, e.g., maximum a posteriori COD for each death given the survey responses.
- the population cause-specific mortality fraction in