dtoa Benchmark

Preamble

This fork of the benchmark was created to demonstrate the performance superiority of my new dtoa() implementation over others.

Ryū algorithm by Ulf Adams known to fastest in much cases, especially for short string representations. However, I would like to draw attention to my own speed-competing but more compact implementation.

Briefly, about this double-to-string implementation:

It is fastest Grisu-based, but not exactly the Grisu3 nor Grisu2;
Compared to Ryū this implementation significantly less in code size and spends less clock cycles per digit, but may slightly inferior in a whole on a 16-17 digit values.
Output string representation always roundtrip convertible to the original value, i.e. strtod() for character string result will return the exactly original value.
Generated string representation is shortest for more than 99.963% of IEEE-754 double values, i.e. one extra digit for less that 0.037% values. Moreover, for less than 0.06% of double values, the last digit differs from an ideal nearest by ±1.
For now produces only a raw ASCII representation, e.g. -22250738585072014e-324 without dot and '\0' at the end;

Now I would like to get feedback, assess how much this is in demand and collect suggestions for further improvements. For instance, I think that it is reasonable to implement conversion with a specified precision (i.e., with a specified number of digits), but not provide a printf-like interface. For more into see issue#1.

Any suggestions are welcome!

Introduction

This benchmark evaluates the performance of conversion from double precision IEEE-754 floating point (double) to ASCII string. The function prototype is:

void dtoa(double value, char* buffer);

The character string result must be convertible to the original value exactly via some correct implementation of strtod(), i.e. roundtrip convertible.

Note that dtoa() is not a standard function in C and C++.

Procedure

Firstly the program verifies the correctness of implementations.

Then, RandomDigit case for benchmark is carried out:

Generates 2000 random double values, filtered out +/-inf and nan. Then convert them to limited precision (1 to 17 decimal digits in significand).
Convert these generated numbers into ASCII.
Each digit group is run for 10000 times. The minimum time duration is measured for 42 trials.

Build and Run

Obtain cmake
Configure build system by running cmake . and build benchmark by running cmake --build .
On success, run the dtoa-benchmark executable is generated at dtoa-benchmark/ or corresponding subdirectory (e.g Release on Windows).
The results in CSV format will be written to dtoa-benchmark/results.
Run GNU make in dtoa-benchmark/results to generate results in HTML.

Results

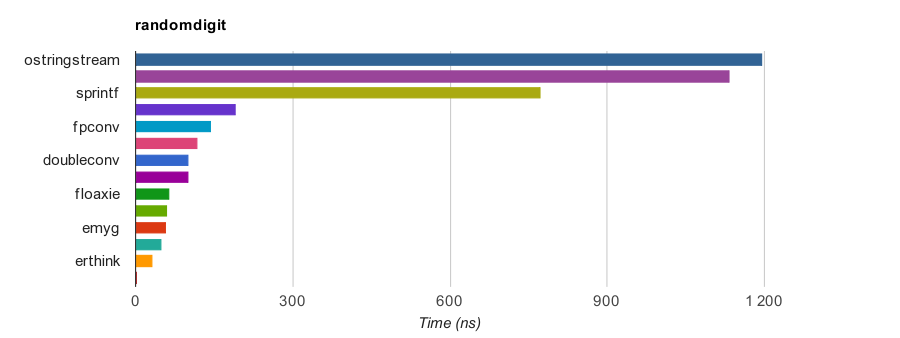
The following are results measured by RandomDigit testcase on a PC (Core i7-7820HQ CPU @ 2.90GHz), where dtoa() is compiled by GNU C++ 9.2.1 for x86-64 Linux. The speedup is based on sprintf's Sum values.

Function	Min ns	RMS ns	Max ns	Sum ns	Speedup
null	1.2	1.200	1.2	20.4	N/A
erthink	21.4	33.381	43.9	558.1	×23.5
ryu	35.3	50.011	65.7	835.4	×15.7
emyg	38.1	58.310	69.7	983.2	×13.3
milo	37.8	59.819	71.8	1007.7	×13.0
floaxie	24.5	68.028	92.4	1089.8	×12.0
fmt	75.3	101.532	130.8	1712.2	×7.7
doubleconv	69.7	103.070	134.0	1731.4	×7.6
grisu2	101.6	119.538	137.8	2024.3	×6.5
fpconv	102.6	145.437	167.5	2454.2	×5.3
stb	188.8	191.082	198.6	3248.1	×4.0
sprintf	700.1	772.833	827.7	13119.8	×1.0
ostrstream	1058.4	1133.081	1187.4	19250.5	×0.7
ostringstream	1110.9	1196.817	1267.8	20327.0	×0.6

All implementations

More clickable charts.

Fastest competitors

Implementations in descending order of speed

Function	Description
erthink	Leonid Yuriev's Grisu-based C++ implementation.
ryu	Ulf Adams's Ryū algorithm.
emyg	C version of Milo Yip's Grisu2 implementation by Doug Currie.
milo	Milo Yip's Grisu2 C++ implementation for RapidJSON.
floaxie	Alexey Chernov's Grisu2 implementation.
fmt	Victor Zverovich's Grisu2 implementation for `{fmt}` C++ library.
doubleconv	C++ implementation extracted from Google's V8 JavaScript Engine with `EcmaScriptConverter().ToShortest()` (based on Grisu3, fall back to slower bignum algorithm when Grisu3 failed to produce shortest implementation).
grisu2	Florian Loitsch's Grisu2 C implementation [1].
fpconv	Andreas Samoljuk's Grisu2 C implementation.
stb	Jeff Roberts's & Sean Barrett's snprintf() implementation.
sprintf	`sprintf()` in C standard library with `"%.17g"` format.
ostringstream	traditional `std::ostringstream` in C++ standard library with `setprecision(17)`.
ostrstream	traditional `std::ostrstream` in C++ standard library with `setprecision(17)`.
~~gay~~	David M. Gay's `dtoa()` C implementation. Disabled because of invalid results and/or SIGSEGV.

FAQ

How to add an implementation?

You may clone an existing implementation file, then modify it and add to CMakeLists.txt. Re-run cmake to re-configure and re-build benchmark. Note that it will automatically register to the benchmark by macro REGISTER_TEST(name).

Making pull request of new implementations is welcome.
Why not converting double to std::string?

It may introduce heap allocation, which is a big overhead. User can easily wrap these low-level functions to return std::string, if needed.
Why fast dtoa() functions is needed?

They are a very common operations in writing data in text format. The standard way of sprintf(), std::stringstream, often provides poor performance. The author of this benchmark would optimize the sprintf implementation in RapidJSON.

References

[1] Loitsch, Florian. "Printing floating-point numbers quickly and accurately with integers." ACM Sigplan Notices 45.6 (2010): 233-243.

Related Benchmarks and Discussions

Printing Floating-Point Numbers

zhiqiang-hhhh/dtoa-benchmark