Welcome to this repo. As the development of geometric deep learning and geometry processing, geometry is playing an ever-growing important role in the field of architecture, computational design, and robotic fabrication. Although I am able to write geometric algorithm from time to time, I aim to have a big and thorough picture over this topic. Therefore, I felt compelled to study computational geometry across different subject.
In light of different sources of materials, this repo is organized as follows:
- Book:books: the must read books
- Lecture:school: the popular online lecture
- Library:computer: the popular geometry processing library
- Paper:page_with_curl: the must read paper
- Workshop:video_camera: the short-period of workshop
My recommended study material is followed:
| Name | Type | Link |
|---|---|---|
| Discrete Differential Geometry, Keenan Crane | Online Lecture | http://geometry.cs.cmu.edu/ddg |
| Digital Geometry Processing, FU Xiaoming | Online Lecture(Chinese) | http://staff.ustc.edu.cn/~fuxm/course/2020_Spring_DGP/index.html |
| Computational Conformal Geometry | Online Lecture | https://www3.cs.stonybrook.edu/~gu/lectures/2020/ |
| Computational Geometry: Algorithms and Applications | Book | https://www.amazon.com/dp/3540779736/ref=cm_sw_em_r_mt_dp_TN2TN09Q61YS2C2D344T |
Discrete Differential Geometry: ➡️(navigate here)
- Chapter 01 Overview
- Chapter 02 Combinatorial Surfaces
- Chapter 03 Intro to Differential Geometry
- Chapter 04 Intro to Exterior Calculus
- Chapter 05 Curvature of Discrete Surfaces
- Chapter 06 The Laplacian
- Chapter 07 Surface Parameterization
- Chapter 08 Vector Field Decomposition and Design
Geometry Modeling and Processing::arrow_right: (navigate here)
➡️(navigate here)
- Mark Meyer, Mathieu Desbrun, Peter Schröder and Alan H. Barr, Discrete Differential-Geometry Operators for Triangulated 2-Manifolds, 2003.
//TODO
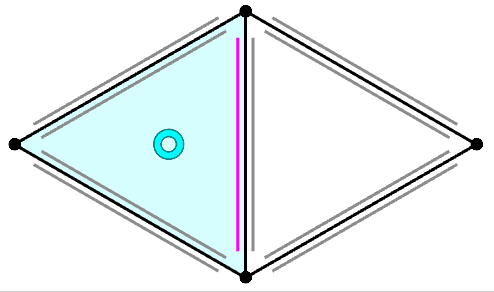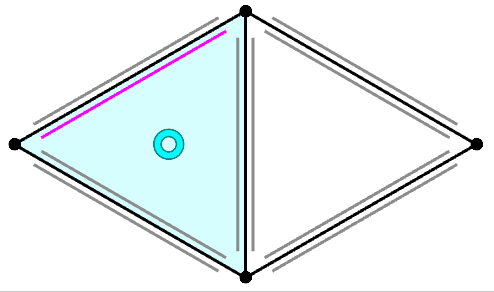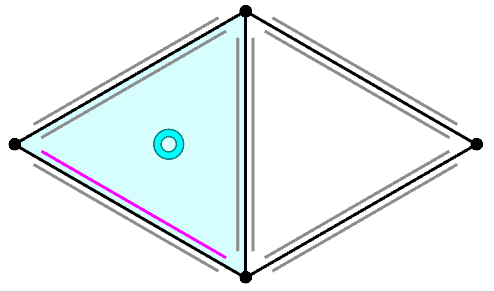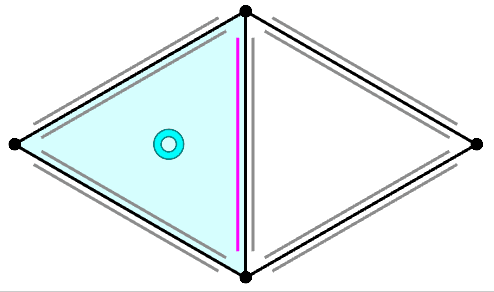 |
 |
|---|---|
| "Next" Operation in HalfEdge data structure | Why tangent vector is orothogonal to normal vector |
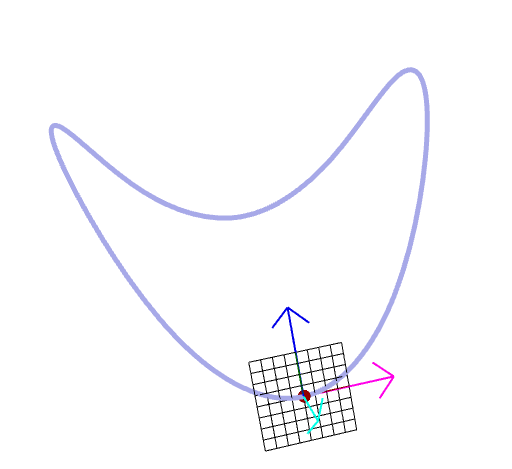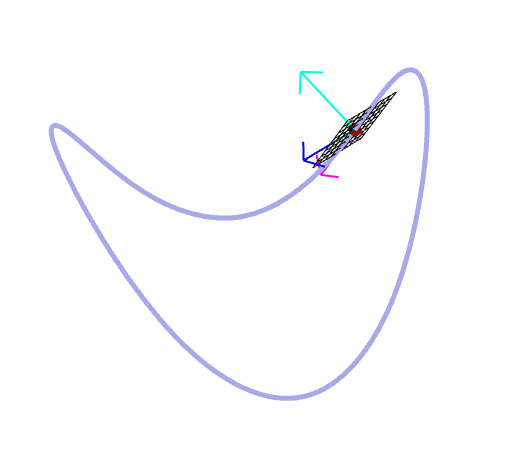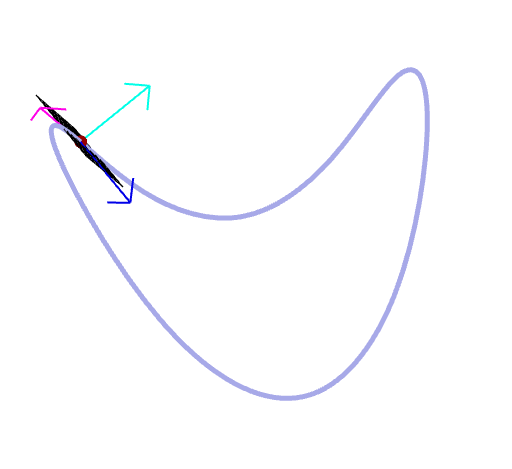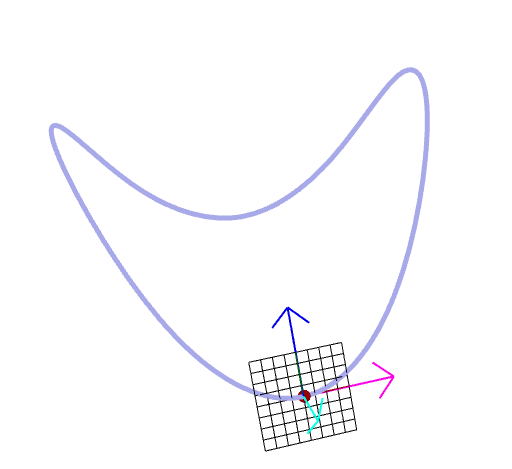 |
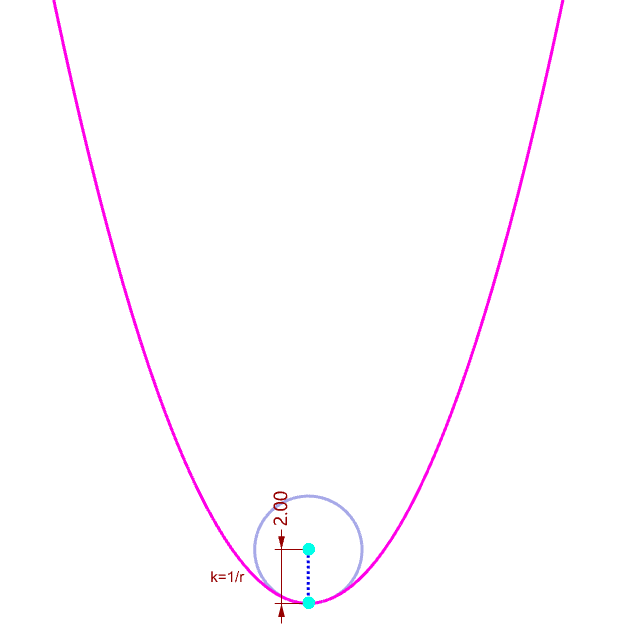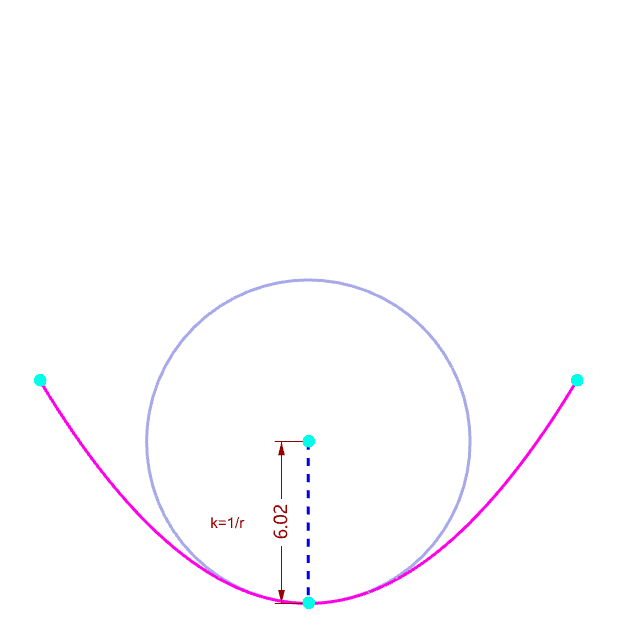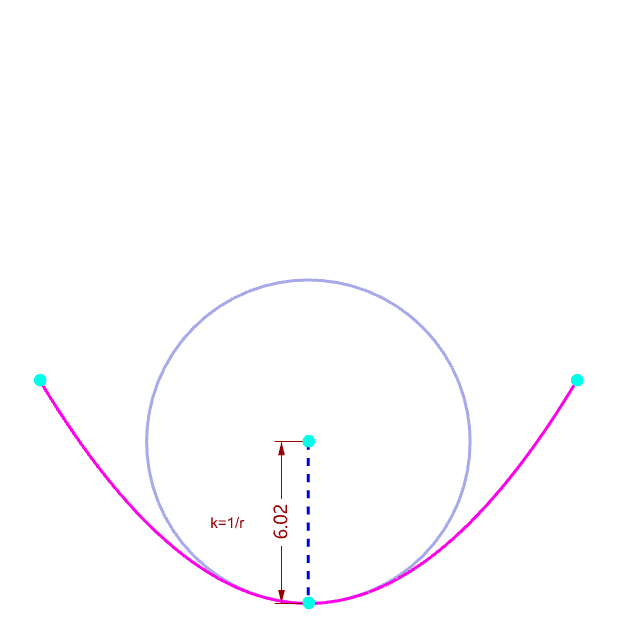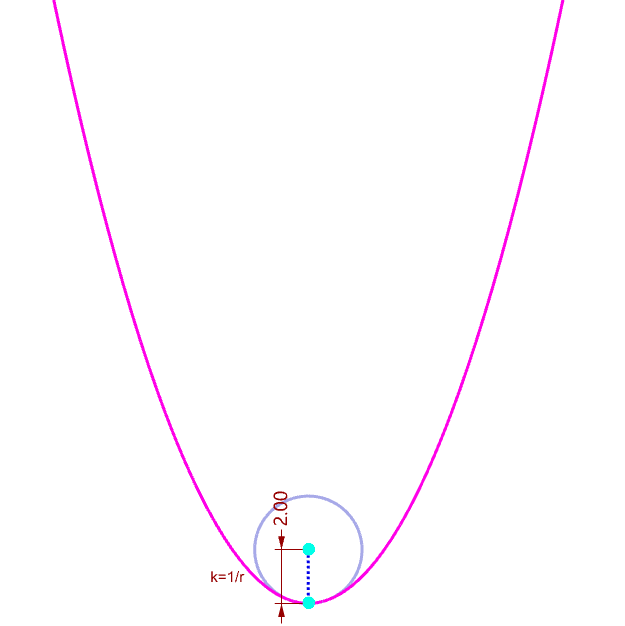 |
|---|---|
| Why tangent vector is orothogonal to normal vector | Visualize the curvature of a curve |
 |
|
|---|---|
| Simplicial Operator written in C++ |
1.This repo is merely a collection of notes and I highly recommend YOU to learn by yourself.
2.The update of this repo may be very very very slow...
3.Please cite the authors for their contribution!