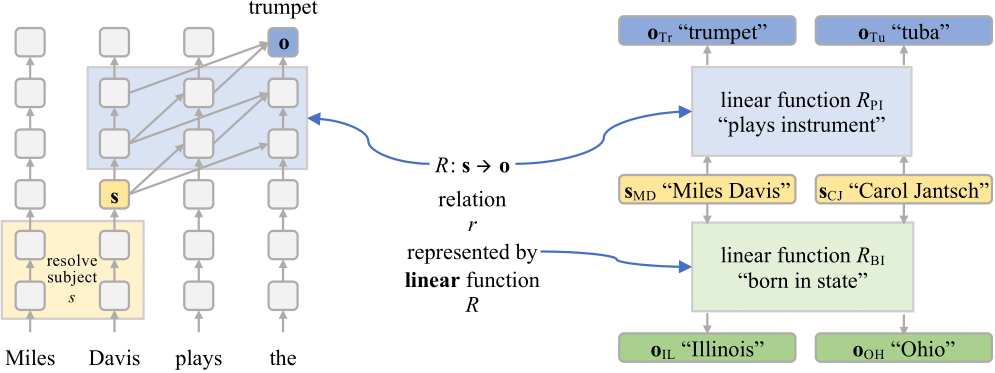
This repository contains the code used for the experiments in the paper Linearity of Relation Decoding in Transformer LMs.
How an LM decodes a relation such as (Miles Davis, plays the instrument, trumpet) involves a sequence of non-linear computations spanning multiple layers. But, in this work we show that for a subset of relations this highly non-linear decoding procedure can be approximated by a simple linear transformation (
Please check lre.baulab.info for more information.
All code is tested on MacOS Ventura (>= 13.1) and Ubuntu 20.04 using Python >= 3.10. It uses a lot of newer Python features, so the Python version is a strict requirement.
To run the code, create a virtual environment with the tool of your choice, e.g. conda:
conda create --name relations python=3.10Then, after entering the environment, install the project dependencies:
python -m pip install invoke
invoke installdemo/demo.ipynb shows how to get
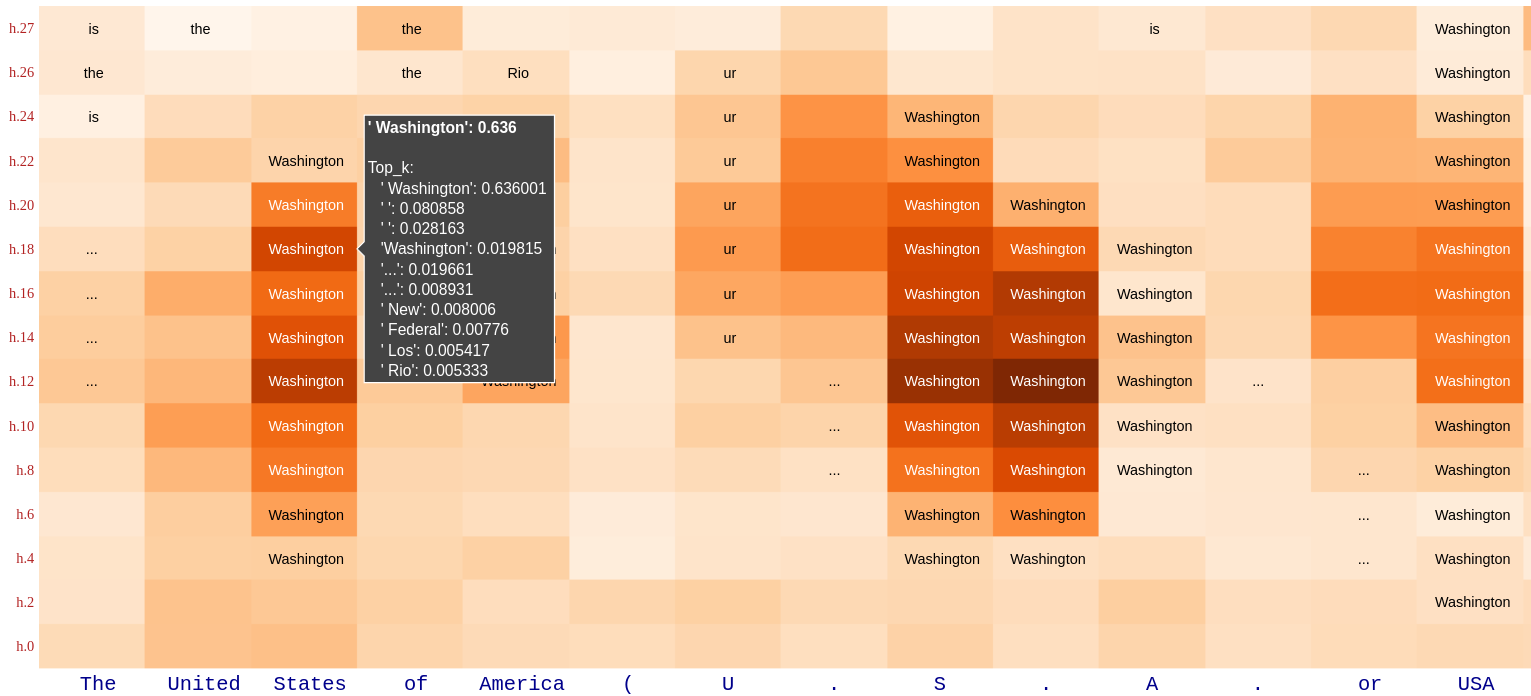
demo/attribute_lens.ipynb demonstrates Attribute Lens, which is motivated by the idea that a hidden state
@article{hernandez2023linearity,
title={Linearity of Relation Decoding in Transformer Language Models},
author={Evan Hernandez and Arnab Sen Sharma and Tal Haklay and Kevin Meng and Martin Wattenberg and Jacob Andreas and Yonatan Belinkov and David Bau},
year={2023},
eprint={2308.09124},
archivePrefix={arXiv},
primaryClass={cs.CL}
}