Implements Low-Rank Adaptation(LoRA) Finetuning from scratch.
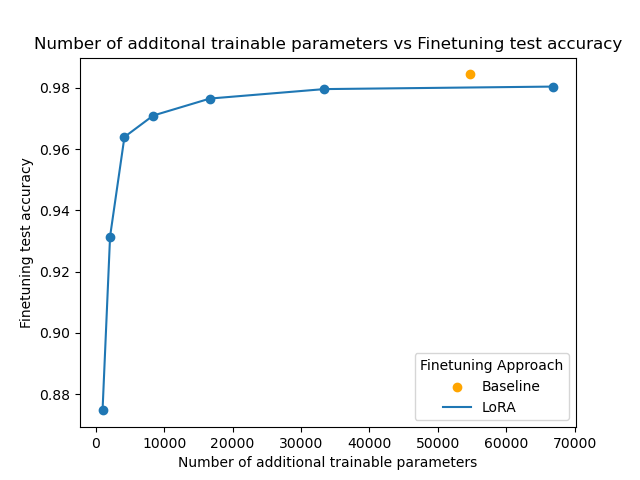
This notebook was a small project to learn more about LoRA finetuning. It implements LoRA from scratch primarily using the paper as a guide. I found that on a simple model, I could achieve 97.9% of the performance of normal finetuning with as little as 7.7% of the trainable weights compared to the traditional approach, which is pretty incredible!
| model | approx. number of trainable parameters | test accuracy | percent trainable parameters relative to baseline | percent test accuracy relative to baseline |
|---|---|---|---|---|
| baseline - whole model finetune | 54700 | 0.984 | N/A | N/A |
| LoRA rank = 1 | 1000 | 0.875 | 1.8% | 88.9% |
| LoRA rank = 2 | 2100 | 0.931 | 3.8% | 94.6% |
| LoRA rank = 4 | 4200 | 0.964 | 7.7% | 97.9% |
| LoRA rank= 8 | 8400 | 0.971 | 15.4% | 98.6% |
| LoRA rank = 16 | 16700 | 0.977 | 30.5% | 99.2% |
| LoRA rank = 32 | 33400 | 0.980 | 61.1% | 99.5% |
| LoRA rank = 64 | 66900 | 0.980 | 122% | 99.6% |
Simplified exerpt from the notebook with a bit of the model:
class LitLoRA(L.LightningModule):
def __init__(self):
super().__init__()
# Define layers for model
self.l1 = nn.Linear(input_size, hidden_size)
self.l2 = nn.Linear(hidden_size, hidden_size)
self.l3 = nn.Linear(hidden_size, self.num_classes)
self.dropout = nn.Dropout(0.1)
self.relu = nn.ReLU()
# Define lora hyperparameters
self.lora_rank = 4 # The rank 'r' for the low-rank adaptation
self.lora_alpha = 1 # lora scaling factor
# layer 1 lora layers
self.l1_lora_A = nn.Parameter(torch.empty(channels * width * height, self.lora_rank))
self.l1_lora_B = nn.Parameter(torch.empty(self.lora_rank, hidden_size))
# layer 2 lora layers
self.l2_lora_A = nn.Parameter(torch.empty(hidden_size, self.lora_rank))
self.l2_lora_B = nn.Parameter(torch.empty(self.lora_rank, hidden_size))
# layer 3 lora layers
self.l3_lora_A = nn.Parameter(torch.empty(hidden_size, self.lora_rank))
self.l3_lora_B = nn.Parameter(torch.empty(self.lora_rank, self.num_classes))
# Initialization for lora layers
for n,p in self.named_parameters():
if 'lora' in n:
if n[-1]=='A':
nn.init.kaiming_uniform_(p, a=math.sqrt(5))
elif n[-1]=='B':
nn.init.zeros_(p)
# freeze non lora weights
for n,p in self.named_parameters():
if 'lora' not in n:
p.requires_grad = False
def lora_linear(self, x, layer, lora_A, lora_B):
# does the work of combining outputs from normal layer and lora layer for x
h = layer(x)
h += x@(lora_A @ lora_B)*self.lora_alpha
return h
def forward(self, x):
# preprocessing
x = torch.flatten(x,1)
# layer 1 (input size, hidden size)
x = self.lora_linear(x, self.l1, self.l1_lora_A, self.l1_lora_B)
x = self.relu(x)
x = self.dropout(x)
# layer 2 (hidden size, hidden size)
x = self.lora_linear(x, self.l2, self.l2_lora_A, self.l2_lora_B)
x = self.relu(x)
x = self.dropout(x)
#layer 3 (hidden size, self.num_classes)
x = self.lora_linear(x, self.l3, self.l3_lora_A, self.l3_lora_B)
return F.log_softmax(x, dim=1)