Due Fri Oct 7, 11:59pm
100 points total + 6 points extra credit
This assignment is intended to help you develop an understanding of the two primary forms of parallel execution present in a modern multi-core CPU:
- SIMD execution within a single processing core
- Parallel execution using multiple cores (You'll see effects of Intel Hyper-threading as well.)
You will also gain experience measuring and reasoning about the performance of parallel programs (a challenging, but important, skill you will use throughout this class). This assignment involves only a small amount of programming, but a lot of analysis!
You will need to run code on the new myth machines for this assignment.
(Hostnames for these machines are myth[51-66].stanford.edu)
These machines contain four-core 4.2 GHz Intel Core i7 processors (although dynamic frequency scaling can take them to 4.5 GHz when the chip decides it is useful and possible to do so). Each core in the processor supports two hardware threads (Intel calls this "Hyper-Threading") and the cores can execute AVX2 vector instructions which describe
simultaneous execution of the same eight-wide operation on multiple single-precision data
values. For the curious, a complete specification for this CPU can be found at
https://ark.intel.com/products/97129/Intel-Core-i7-7700K-Processor-8M-Cache-up-to-4-50-GHz-. Students that want to dig deeper might enjoy this writeup.
Note: For grading purposes, we expect you to report on the performance of code run on the Stanford myth machines, however for kicks, you may also want to run the programs in this assignment on your own machine. (You will first need to install the Intel SPMD Program Compiler (ISPC) available here: http://ispc.github.io/). Feel free to include your findings from running code on other machines in your report as well, just be very clear what machine you were running on.
To get started:
- ISPC is needed to compile many of the programs used in this assignment. ISPC can be easily installed on the myth machines through the following steps:
From a myth machine, download the linux binary into a local directory of your choice. You can get ISPC compiler binaries for Linux from the ISPC downloads page. From myth, we recommend you use wget to directly download the binary from the downloads page. As of Fall 2022 Week 1, the wget line below works:
wget https://github.com/ispc/ispc/releases/download/v1.18.0/ispc-v1.18.0-linux.tar.gz
Untar the downloaded file: tar -xvf ispc-v1.18.0-linux.tar.gz
Add the ISPC bin directory to your system path. For example, if untarring the downloaded file produces the directory ~/Downloads/ispc-v1.18.0-linux, in bash you'd update your path variable with:
export PATH=$PATH:${HOME}/Downloads/ispc-v1.18.0-linux/bin
The above line can be added to your .bashrc file for permanence.
If you are using csh, you'll update your PATH using setenv. A quick Google search will teach you how.
-
The assignment starter code is available on https://github.com/stanford-cs149/asst1. Please clone the Assignment 1 starter code using:
git clone https://github.com/stanford-cs149/asst1.git
Build and run the code in the prog1_mandelbrot_threads/ directory of
the code base. (Type make to build, and ./mandelbrot to run it.)
This program produces the image file mandelbrot-serial.ppm, which is a visualization of a famous set of
complex numbers called the Mandelbrot set. (Most platforms have a .ppm
view. For example, to view the resulting images remotely, use ssh -Y
and the display command.) As you can see in the images below, the
result is a familiar and beautiful fractal. Each pixel in the image
corresponds to a value in the complex plane, and the brightness of
each pixel is proportional to the computational cost of determining
whether the value is contained in the Mandelbrot set. To get image 2,
use the command option --view 2. (See function mandelbrotSerial()
defined in mandelbrotSerial.cpp). You can learn more about the
definition of the Mandelbrot set at
http://en.wikipedia.org/wiki/Mandelbrot_set.
Your job is to parallelize the computation of the images using
std::thread. Starter
code that spawns one additional thread is provided in the function
mandelbrotThread() located in mandelbrotThread.cpp. In this function, the
main application thread creates another additional thread using the constructor
std::thread(function, args...) It waits for this thread to complete by calling
join on the thread object.
Currently the launched thread does not do any computation and returns immediately.
You should add code to workerThreadStart function to accomplish this task.
You will not need to make use of any other std::thread API calls in this assignment.
What you need to do:
- Modify the starter code to parallelize the Mandelbrot generation using two processors. Specifically, compute the top half of the image in thread 0, and the bottom half of the image in thread 1. This type of problem decomposition is referred to as spatial decomposition since different spatial regions of the image are computed by different processors.
- Extend your code to use 2, 3, 4, 5, 6, 7, and 8 threads, partitioning the image generation work accordingly (threads should get blocks of the image). Note that the processor only has four cores but each core supports two hyper-threads, so it can execute a total of eight threads interleaved on its execution contents. In your write-up, produce a graph of speedup compared to the reference sequential implementation as a function of the number of threads used FOR VIEW 1. Is speedup linear in the number of threads used? In your writeup hypothesize why this is (or is not) the case? (you may also wish to produce a graph for VIEW 2 to help you come up with a good answer. Hint: take a careful look at the three-thread datapoint.)
- To confirm (or disprove) your hypothesis, measure the amount of time
each thread requires to complete its work by inserting timing code at
the beginning and end of
workerThreadStart(). How do your measurements explain the speedup graph you previously created? - Modify the mapping of work to threads to achieve to improve speedup to at about 7-8x on both views of the Mandelbrot set (if you're above 7x that's fine, don't sweat it). You may not use any synchronization between threads in your solution. We are expecting you to come up with a single work decomposition policy that will work well for all thread counts---hard coding a solution specific to each configuration is not allowed! (Hint: There is a very simple static assignment that will achieve this goal, and no communication/synchronization among threads is necessary.). In your writeup, describe your approach to parallelization and report the final 8-thread speedup obtained.
- Now run your improved code with 16 threads. Is performance noticably greater than when running with eight threads? Why or why not?
Take a look at the function clampedExpSerial in prog2_vecintrin/main.cpp of the
Assignment 1 code base. The clampedExp() function raises values[i] to the power given by exponents[i] for all elements of the input array and clamps the resulting values at 9.999999. In program 2, your job is to vectorize this piece of code so it can be run on a machine with SIMD vector instructions.
However, rather than craft an implementation using SSE or AVX2 vector intrinsics that map to real SIMD vector instructions on modern CPUs, to make things a little easier, we're asking you to implement your version using CS149's "fake vector intrinsics" defined in CS149intrin.h. The CS149intrin.h library provides you with a set of vector instructions that operate
on vector values and/or vector masks. (These functions don't translate to real CPU vector instructions, instead we simulate these operations for you in our library, and provide feedback that makes for easier debugging.) As an example of using the CS149 intrinsics, a vectorized version of the abs() function is given in main.cpp. This example contains some basic vector loads and stores and manipulates mask registers. Note that the abs() example is only a simple example, and in fact the code does not correctly handle all inputs! (We will let you figure out why!) You may wish to read through all the comments and function definitions in CS149intrin.h to know what operations are available to you.
Here are few hints to help you in your implementation:
- Every vector instruction is subject to an optional mask parameter. The mask parameter defines which lanes whose output is "masked" for this operation. A 0 in the mask indicates a lane is masked, and so its value will not be overwritten by the results of the vector operation. If no mask is specified in the operation, no lanes are masked. (Note this equivalent to providing a mask of all ones.) Hint: Your solution will need to use multiple mask registers and various mask operations provided in the library.
- Hint: Use
_cs149_cntbitsfunction helpful in this problem. - Consider what might happen if the total number of loop iterations is not a multiple of SIMD vector width. We suggest you test
your code with
./myexp -s 3. Hint: You might find_cs149_init_oneshelpful. - Hint: Use
./myexp -lto print a log of executed vector instruction at the end. Use functionaddUserLog()to add customized debug information in log. Feel free to add additionalCS149Logger.printLog()to help you debug.
The output of the program will tell you if your implementation generates correct output. If there are incorrect results, the program will print the first one it finds and print out a table of function inputs and outputs. Your function's output is after "output = ", which should match with the results after "gold = ". The program also prints out a list of statistics describing utilization of the CS149 fake vector units. You should consider the performance of your implementation to be the value "Total Vector Instructions". (You can assume every CS149 fake vector instruction takes one cycle on the CS149 fake SIMD CPU.) "Vector Utilization" shows the percentage of vector lanes that are enabled.
What you need to do:
- Implement a vectorized version of
clampedExpSerialinclampedExpVector. Your implementation should work with any combination of input array size (N) and vector width (VECTOR_WIDTH). - Run
./myexp -s 10000and sweep the vector width from 2, 4, 8, to 16. Record the resulting vector utilization. You can do this by changing the#define VECTOR_WIDTHvalue inCS149intrin.h. Does the vector utilization increase, decrease or stay the same asVECTOR_WIDTHchanges? Why? - Extra credit: (1 point) Implement a vectorized version of
arraySumSerialinarraySumVector. Your implementation may assume thatVECTOR_WIDTHis a factor of the input array sizeN. Whereas the serial implementation hasO(N)span, your implementation should have at mostO(N / VECTOR_WIDTH + log2(VECTOR_WIDTH))span. You may find thehaddandinterleaveoperations useful.
Now that you're comfortable with SIMD execution, we'll return to parallel Mandelbrot fractal generation (like in program 1). Like Program 1, Program 3 computes a mandelbrot fractal image, but it achieves even greater speedups by utilizing both the CPU's four cores and the SIMD execution units within each core.
In Program 1, you parallelized image generation by creating one thread for each processing core in the system. Then, you assigned parts of the computation to each of these concurrently executing threads. (Since threads were one-to-one with processing cores in Program 1, you effectively assigned work explicitly to cores.) Instead of specifying a specific mapping of computations to concurrently executing threads, Program 3 uses ISPC language constructs to describe independent computations. These computations may be executed in parallel without violating program correctness (and indeed they will!). In the case of the Mandelbrot image, computing the value of each pixel is an independent computation. With this information, the ISPC compiler and runtime system take on the responsibility of generating a program that utilizes the CPU's collection of parallel execution resources as efficiently as possible.
You will make a simple fix to Program 3 which is written in a combination of
C++ and ISPC (the error causes a performance problem, not a correctness one).
With the correct fix, you should observe performance that is over 32 times
greater than that of the original sequential Mandelbrot implementation from
mandelbrotSerial().
When reading ISPC code, you must keep in mind that although the code appears
much like C/C++ code, the ISPC execution model differs from that of standard
C/C++. In contrast to C, multiple program instances of an ISPC program are
always executed in parallel on the CPU's SIMD execution units. The number of
program instances executed simultaneously is determined by the compiler (and
chosen specifically for the underlying machine). This number of concurrent
instances is available to the ISPC programmer via the built-in variable
programCount. ISPC code can reference its own program instance identifier via
the built-in programIndex. Thus, a call from C code to an ISPC function can
be thought of as spawning a group of concurrent ISPC program instances
(referred to in the ISPC documentation as a gang). The gang of instances
runs to completion, then control returns back to the calling C code.
Stop. This is your friendly instructor. Please read the preceding paragraph again. Trust me.
As an example, the following program uses a combination of regular C code and ISPC code to add two 1024-element vectors. As we discussed in class, since each instance in a gang is independent and performing the exact same program logic, execution can be accelerated via implementation using SIMD instructions.
A simple ISPC program is given below. The following C code will call the following ISPC code:
------------------------------------------------------------------------
C program code: myprogram.cpp
------------------------------------------------------------------------
const int TOTAL_VALUES = 1024;
float a[TOTAL_VALUES];
float b[TOTAL_VALUES];
float c[TOTAL_VALUES]
// Initialize arrays a and b here.
sum(TOTAL_VALUES, a, b, c);
// Upon return from sumArrays, result of a + b is stored in c.
The corresponding ISPC code:
------------------------------------------------------------------------
ISPC code: myprogram.ispc
------------------------------------------------------------------------
export sum(uniform int N, uniform float* a, uniform float* b, uniform float* c)
{
// Assumption programCount divides N evenly.
for (int i=0; i<N; i+=programCount)
{
c[programIndex + i] = a[programIndex + i] + b[programIndex + i];
}
}
The ISPC program code above interleaves the processing of array elements among program instances. Note the similarity to Program 1, where you statically assigned parts of the image to threads.
However, rather than thinking about how to divide work among program instances
(that is, how work is mapped to execution units), it is often more convenient,
and more powerful, to instead focus only on the partitioning of a problem into
independent parts. ISPCs foreach construct provides a mechanism to express
problem decomposition. Below, the foreach loop in the ISPC function sum2
defines an iteration space where all iterations are independent and therefore
can be carried out in any order. ISPC handles the assignment of loop iterations
to concurrent program instances. The difference between sum and sum2 below
is subtle, but very important. sum is imperative: it describes how to
map work to concurrent instances. The example below is declarative: it
specifies only the set of work to be performed.
-------------------------------------------------------------------------
ISPC code:
-------------------------------------------------------------------------
export sum2(uniform int N, uniform float* a, uniform float* b, uniform float* c)
{
foreach (i = 0 ... N)
{
c[i] = a[i] + b[i];
}
}
Before proceeding, you are encouraged to familiarize yourself with ISPC
language constructs by reading through the ISPC walkthrough available at
http://ispc.github.io/example.html. The example program in the walkthrough
is almost exactly the same as Program 3's implementation of mandelbrot_ispc()
in mandelbrot.ispc. In the assignment code, we have changed the bounds of
the foreach loop to yield a more straightforward implementation.
What you need to do:
- Compile and run the program mandelbrot ispc. The ISPC compiler is currently configured to emit 8-wide AVX2 vector instructions. What is the maximum speedup you expect given what you know about these CPUs? Why might the number you observe be less than this ideal? (Hint: Consider the characteristics of the computation you are performing? Describe the parts of the image that present challenges for SIMD execution? Comparing the performance of rendering the different views of the Mandelbrot set may help confirm your hypothesis.).
We remind you that for the code described in this subsection, the ISPC compiler maps gangs of program instances to SIMD instructions executed on a single core. This parallelization scheme differs from that of Program 1, where speedup was achieved by running threads on multiple cores.
If you look into detailed technical material about the CPUs in the myth machines, you will find there are a complicated set of rules about how many scalar and vector instructions can be run per clock. For the purposes of this assignment, you can assume that there are about as many 8-wide vector execution units as there are scalar execution units for floating point math.
ISPCs SPMD execution model and mechanisms like foreach facilitate the creation
of programs that utilize SIMD processing. The language also provides an additional
mechanism utilizing multiple cores in an ISPC computation. This mechanism is
launching ISPC tasks.
See the launch[2] command in the function mandelbrot_ispc_withtasks. This
command launches two tasks. Each task defines a computation that will be
executed by a gang of ISPC program instances. As given by the function
mandelbrot_ispc_task, each task computes a region of the final image. Similar
to how the foreach construct defines loop iterations that can be carried out
in any order (and in parallel by ISPC program instances, the tasks created by
this launch operation can be processed in any order (and in parallel on
different CPU cores).
What you need to do:
- Run
mandelbrot_ispcwith the parameter--tasks. What speedup do you observe on view 1? What is the speedup over the version ofmandelbrot_ispcthat does not partition that computation into tasks? - There is a simple way to improve the performance of
mandelbrot_ispc --tasksby changing the number of tasks the code creates. By only changing code in the functionmandelbrot_ispc_withtasks(), you should be able to achieve performance that exceeds the sequential version of the code by over 32 times! How did you determine how many tasks to create? Why does the number you chose work best? - Extra Credit: (2 points) What are differences between the thread abstraction (used in Program 1) and the ISPC task abstraction? There are some obvious differences in semantics between the (create/join and (launch/sync) mechanisms, but the implications of these differences are more subtle. Here's a thought experiment to guide your answer: what happens when you launch 10,000 ISPC tasks? What happens when you launch 10,000 threads? (For this thought experiment, please discuss in the general case
- i.e. don't tie your discussion to this given mandelbrot program.)
The smart-thinking student's question: Hey wait! Why are there two different
mechanisms (foreach and launch) for expressing independent, parallelizable
work to the ISPC system? Couldn't the system just partition the many iterations
of foreach across all cores and also emit the appropriate SIMD code for the
cores?
Answer: Great question! And there are a lot of possible answers. Come to office hours.
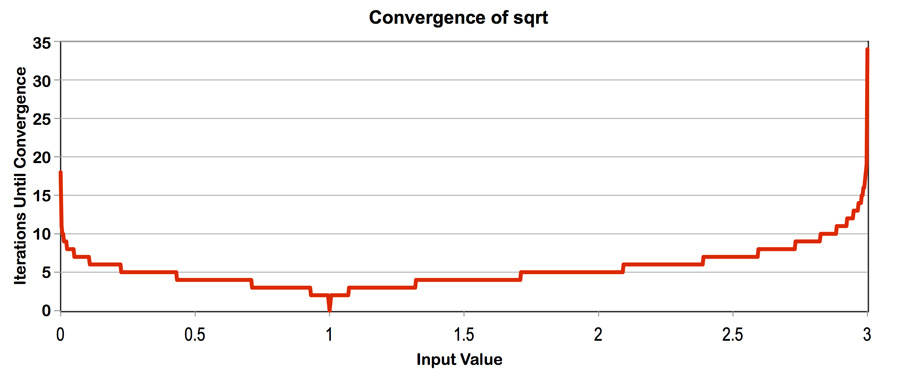
Program 4 is an ISPC program that computes the square root of 20 million
random numbers between 0 and 3. It uses a fast, iterative implementation of
square root that uses Newton's method to solve the equation sqrt to converge to an accurate solution
for values in the (0-3) range. (The implementation does not converge for
inputs outside this range). Notice that the speed of convergence depends on the
accuracy of the initial guess.
Note: This problem is a review to double-check your understanding, as it covers similar concepts as programs 2 and 3.
What you need to do:
- Build and run
sqrt. Report the ISPC implementation speedup for single CPU core (no tasks) and when using all cores (with tasks). What is the speedup due to SIMD parallelization? What is the speedup due to multi-core parallelization? - Modify the contents of the array values to improve the relative speedup of the ISPC implementations. Construct a specifc input that maximizes speedup over the sequential version of the code and report the resulting speedup achieved (for both the with- and without-tasks ISPC implementations). Does your modification improve SIMD speedup? Does it improve multi-core speedup (i.e., the benefit of moving from ISPC without-tasks to ISPC with tasks)? Please explain why.
- Construct a specific input for
sqrtthat minimizes speedup for ISPC (without-tasks) over the sequential version of the code. Describe this input, describe why you chose it, and report the resulting relative performance of the ISPC implementations. What is the reason for the loss in efficiency? (keep in mind we are using the--target=avx2option for ISPC, which generates 8-wide SIMD instructions). - Extra Credit: (up to 2 points) Write your own version of the
sqrtfunction manually using AVX2 intrinsics. To get credit your implementation should be nearly as fast (or faster) than the binary produced using ISPC. You may find the Intel Intrinsics Guide very helpful.
Program 5 is an implementation of the saxpy routine in the BLAS (Basic Linear
Algebra Subproblems) library that is widely used (and heavily optimized) on
many systems. saxpy computes the simple operation result = scale*X+Y, where X, Y,
and result are vectors of N elements (in Program 5, N = 20 million) and scale is a scalar. Note that
saxpy performs two math operations (one multiply, one add) for every three
elements used. saxpy is a trivially parallelizable computation and features predictable, regular data access and predictable execution cost.
What you need to do:
- Compile and run
saxpy. The program will report the performance of ISPC (without tasks) and ISPC (with tasks) implementations of saxpy. What speedup from using ISPC with tasks do you observe? Explain the performance of this program. Do you think it can be substantially improved? (For example, could you rewrite the code to achieve near linear speedup? Yes or No? Please justify your answer.) - Extra Credit: (1 point) Note that the total memory bandwidth consumed computation in
main.cppisTOTAL_BYTES = 4 * N * sizeof(float);. Even thoughsaxpyloads one element from X, one element from Y, and writes one element toresultthe multiplier by 4 is correct. Why is this the case? (Hint, think about how CPU caches work.) - Extra Credit: (points handled on a case-by-case basis) Improve the performance of
saxpy. We're looking for a significant speedup here, not just a few percentage points. If successful, describe how you did it and what a best-possible implementation on these systems might achieve. Also, if successful, come tell the staff, we'll be interested. ;-)
Notes: Some students have gotten hung up on this question (thinking too hard) in the past. We expect a simple answer, but the results from running this problem might trigger more questions in your head. Feel encouraged to come talk to the staff.
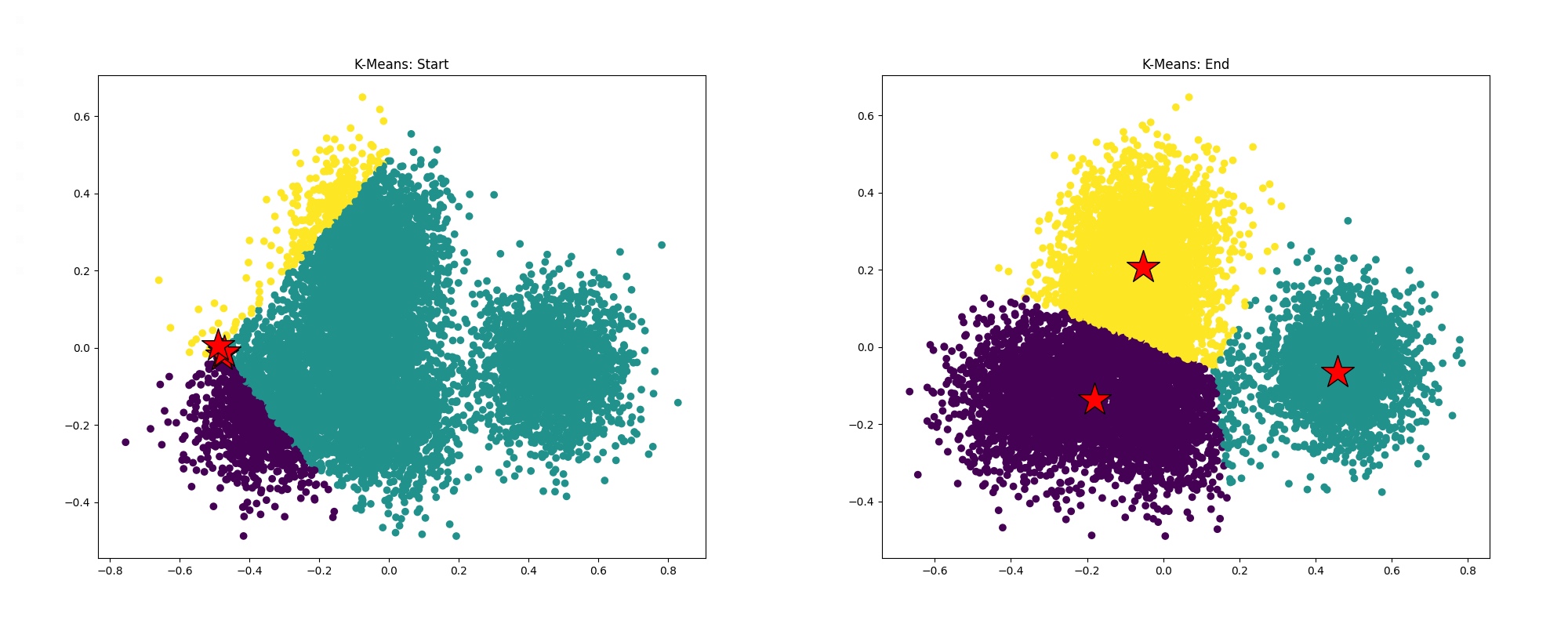
Program 6 clusters one million data points using the K-Means data clustering algorithm (Wikipedia, CS 221 Handout). If you're unfamiliar with the algorithm, don't worry! The specifics aren't important to the exercise, but at a high level, given K starting points (cluster centroids), the algorithm iteratively updates the centroids until a convergence criteria is met. The results can be seen in the below images depicting the state of the algorithm at the beginning and end of the program, where red stars are cluster centroids and the data point colors correspond to cluster assignments.
In the starter code you have been given a correct implementation of the K-means algorithm, however in its current state it is not quite as fast as we would like it to be. This is where you come in! Your job will be to figure out where the implementation needs to be improved and how to improve it. The key skill you will practice in this problem is isolating a performance hotspot. We aren't going to tell you where to look in the code. You need to figure it out. Your first thought should be... where is the code spending the most time and you should insert timing code into the source to make measurements. Based on these measurements, you should focus in on the part of the code that is taking a significant portion of the runtime, and then understand it more carefully to determine if there is a way to speed it up.
What you need to do:
- Use the command
ln -s /afs/ir.stanford.edu/class/cs149/data/data.dat ./data.datto create a symbolic link to the dataset in your current directory (make sure you're in theprog6_kmeansdirectory). This is a large file (~800MB), so this is the preferred way to access it. However, if you'd like a local copy, you can run this command on your personal machinescp [Your SUNetID]@myth[51-66].stanford.edu:/afs/ir.stanford.edu/class/cs149/data/data.dat ./data.dat. Once you have the data, compile and runkmeans(it may take longer than usual for the program to load the data on your first try). The program will report the total runtime of the algorithm on the data. - Run
pip install -r requirements.txtto download the necessary plotting packages. Next, try runningpython3 plot.pywhich will generate the files "start.png" and "end.png" from the logs ("start.log" and "end.log") generated from runningkmeans. These files will be in the current directory and should look similar to the above images. Warning: You might notice that not all points are assigned to the "closest" centroid. This is okay. (For those that want to understand why: We project 100-dimensional datapoints down to 2-D using PCA to produce these visualizations. Therefore, while the 100-D datapoint is near the appropriate centroid in high dimensional space, the projects of the datapoint and the centroid may not be close to each other in 2-D.). As long as the clustering looks "reasonable" (use the images produced by the starter code in step 2 as a reference) and most points appear to be assigned to the clostest centroid, the code remains correct. - Utilize the timing function in
common/CycleTimer.hto determine where in the code there are performance bottlenecks. You will need to callCycleTimer::currentSeconds(), which returns the current time (in seconds) as a floating point number. Where is most of the time being spent in the code? - Based on your findings from the previous step, improve the implementation. We are looking for a speedup of about 2.1x or more (i.e
$\frac{oldRuntime}{newRuntime} >= 2.1$ ). Please explain how you arrived at your solution, as well as what your final solution is and the associated speedup. The writeup of this process should describe a sequence of steps. We expect something of the form "I measured ... which let me to believe X. So to improve things I tried ... resulting in a speedup/slowdown of ...".
Constraints:
- You may only modify code in
kmeansThread.cpp. You are not allowed to modify thestoppingConditionMetfunction and you cannot change the interface tokMeansThread, but anything is fair game (e.g. you can add new members to theWorkerArgsstruct, rewrite functions, allocate new arrays, etc.). However... - Make sure you do not change the functionality of the implementation! If the algorithm doesn't converge or the result from running
python3 plot.pydoes not look like what's produced by the starter code, something is wrong! For example, you cannot simply remove the main "while" loop or change the semantics of thedistfunction, since this would yield incorrect results. - Important: you may only parallelize one of the following functions:
dist,computeAssignments,computeCentroids,computeCost. For an example of how to write parallel code usingstd::thread, seeprog1_mandelbrot_threads/mandelbrotThread.cpp.
Tips / Notes:
- This problem should not require a significant amount of coding. Our solution modified/added around 20-25 lines of code.
- Once you've used timers to isolate hotspots, to improve the code make sure you understand the relative sizes of K, M, and N.
- Try to prioritize code improvements with the potential for high returns and think about the different axes of parallelism available in the problem and how you may take advantage of them.
- The objective of this program is to give you more practice with learning how to profile and debug performance oriented programs. Even if you don't hit the performance target, if you demonstrate good/thoughtful debugging skills in the writeup you'll still get most of the points.
For those with access to newer hardware, try changing the compilation target to ARM, and produce a report of performance of the various programs on a new Apple ARM-based laptop. The staff is curious about what you will find. What speedups are you observing from SIMD execution? Those without access to a modern Macbook could use the ARM-based servers that are available on a cloud provider like AWS.
Handin will be performed via Gradescope. Only one handin per group is required. Please place the following files in your handin:
- Your writeup, in a file called writeup.pdf
- In your writeup, please make sure both group members' names and SUNet id's are in the document. (if you are a group of two)
- Your implementation of main.cpp in Program 2, in a file called
prob2.cpp - Your implementation of kmeansThread.cpp in Program 6, in a file called
prob6.cpp
If you would like to hand in additional code, for example, because you attempted an extra credit, you are free to include that as well. Please tell the CAs to look for your extra credit. When handed in, all code must be compilable and runnable out of the box on the myth machines!
- Extensive ISPC documentation and examples can be found at http://ispc.github.io/
- Zooming into different locations of the mandelbrot image can be quite fascinating
- Intel provides a lot of supporting material about AVX2 vector instructions at http://software.intel.com/en-us/avx/.
- The Intel Intrinsics Guide is very useful.