/elm-faster-map

Primary LanguageElm

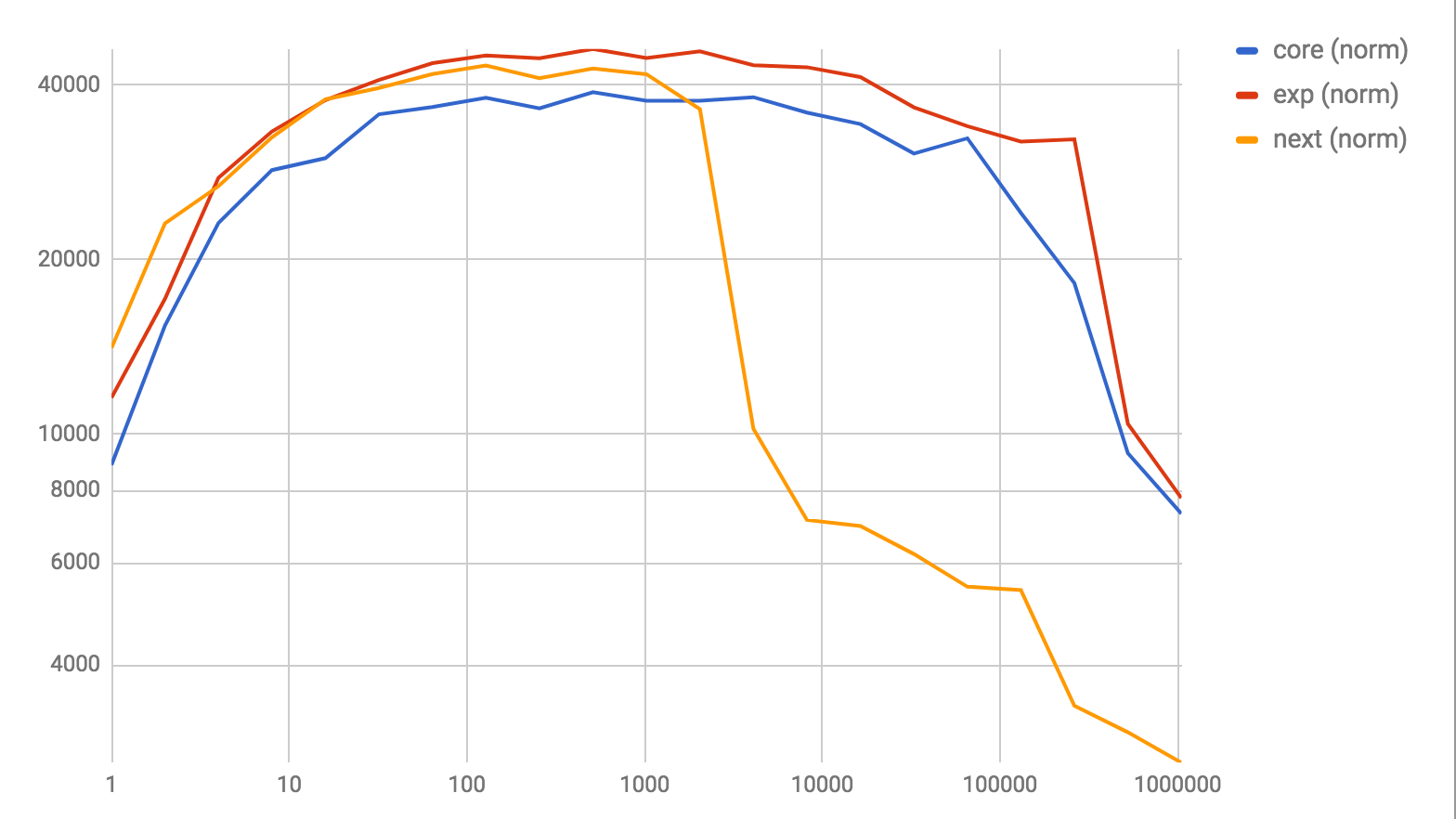
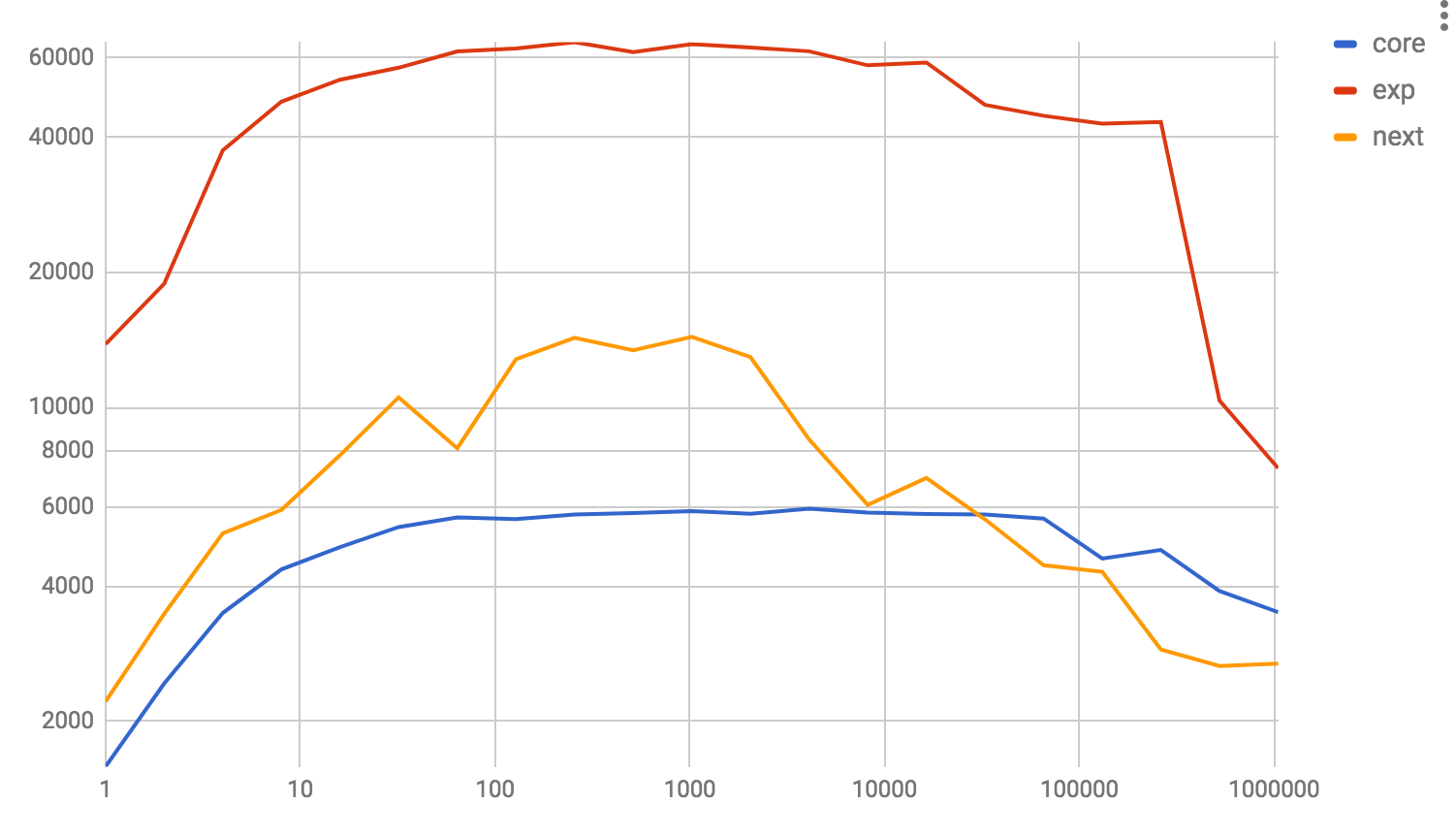
Fast List.foldr and List.map implementations.

List.foldr

map higher is better

List.map

map higher is better

What?

Both charts show a normalized view of how many cons-cells were processed per second by the relevant implementation, on a logarithmic scale - both vertically and horizontally.

The implementations are as follows

  • core corresponds to the current 0.18 core implementation
  • next corresponds to what's currently pending for 0.19
  • experiment corresponds to this repository

The idea is applied directly to List.map as well, rather than implementing it in terms of foldr. This should at least partially explain the discrepancy there.

Note: the next implementation drops off at the 2000-elements mark, as that's the point where it falls back to a naive, stack-safe implementation.

How?

A first realization:

List.map over a List of a known length is (which is more or less the same thing as a tuple) is easy: we just unroll the whole thing and apply the mapping function to each entry:

For example, let's assume we're only dealing with tuples of 3 entries.

map : (a -> b) -> (a, a, a) -> List b
map op ( a, b, c ) =
  op a :: op b :: op c :: []

Now, our list doesn't look like that, but we can create a pair of functions to first split our list into such chunks, and then map each such chunk, building up the final result.

More importantly, we can write this in a way that both functions can have tail calls eliminated.

Note: We're completely ignore what happens if our list doesn't happen to exist of a X•N entries, with N the number of entries each tuple holds. This is just for illustration.

makeChunksAndMap : (a -> b) -> List a -> List (a, a, a) -> List b
makeChunksAndMap op list acc =
    case list of
        a :: b :: c :: xs ->
            makeChunks op xs (( a, b, c ) :: acc)

        _ ->
            mapChunks op acc []

mapChunks : (a -> b) -> List (a, a, a) -> List b -> List b
mapChunks op chunkList acc =
    case chunkList of
        ( a, b, c ) :: xs ->
            mapChunks op xs ( op a :: op b :: op c :: acc )

        _ ->
            acc

Note that it's pretty trivial to make this work properly for lists of length that doesn't happen to be a multiple of N by passing in the remaining N-1 elements with op already applied as the accumulator for mapChunks.

Now, why would this be fast to begin with? Essentially we're minimizing the number of full traversals we need. With N = 1, the described pattern would essentially be reversing the list and doing a foldl over it, which needs 2 full traversals and needs to consider each element separately.

However, for N = 2, this already halves the number of full traversals we need to do, at the cost of more pattern matching. Note that the time complexity for both is the same - we're still going O(2n) - however the constant factors involved are quite different. Function calls are very expensive, while pattern matching is relatively cheap.

So, the challenge is finding an N that provides a good balance between the cost of the required pattern-matching, and the savings by limiting the number of full traversals we need.

Additionally, a higher N means more code.

However there is a second, more hidden cost: we're allocating a bunch of extra datastructures - those tuples each take up some memory, and we're holding n // N of these in memory. The actual act of constructing a tuple also comes at a cost!

So here's a second realization: we can keep the tails of the list in memory, and pattern match on those in mapChunks. Since we've already proven that each tail holds the appropriate number of elements, this means we only pay the cost of pattern-matching twice. Since lists are a nested datastructure, holding on to a "subtree" of that costs no more than a single pointer.

Consider an input list like so:

a :: b :: c :: d :: e :: f :: g :: h :: i :: j :: []

We can represent the tails with pointers to these elements, for N = 3

a :: b :: c :: d :: e :: f :: g :: h :: i :: j :: []
^---------------------------------------------------
               ^------------------------------------
                              ^---------------------
                                             ^------

With tuples, for a list of length X, we keep a list of X // N tuples in memory, each with N pointers to the contained data. So essentially, we're duplicating the entire list in memory while chunking, with some added overhead to actually construct tuples.

With tails, we keep just X // N tails in memory, each a single pointer to a specific tail.

Using that strategy, the challenge changes a little, since the impact of pattern-matching is now paid twice.

Credits

Based on https://twitter.com/antron__/status/910894281593942017

Running the benchmarks

  • Go into bench
  • run ./run.sh MapBench.elm to compare map performance
  • run ./run.sh FoldrBench.elm to compare foldr performance
  • run ./run.sh MapDepth.elm to compare performance for how deep we pattern match things

Fair warning: these take a while.

TODO