This is Yune's Leetcode repo. I build this repo to help cs and cs align students in northeastern university to better crack leetcode solution. Some of the code is still navie and perhaps not the best way. I still have a long path to walk ahead. But The repo implement a template idea. There are currently 80 more leetcode solution in the repo.
All the code here is according to labuladong, but a python version. If you were a labuladong reader , but you prefer to use python as your weapon on leetcode. You are in the right battle field.
I build this repo initially in this organization, If you want to check some template written in python. Go to issue tab . If you want to check the solution of certain leetcode question, just click on solution.
Rule No.1
- Don't be a coward before algorithem problems. Show me your gut, and let's fuck algorithem.
Rule No.2
- Talk is cheap, Code is valuable. So Shut The Fuck Up. 《话越多越菜》
复习 第一轮()
- merge-k-sorted-lists solution
- merge-two-sorted-lists solution
- remove-nth-node-from-end-of-list solution 先后指针
- middle-of-the-linked-list solution 快慢指针
- linked-list-cycle solution 快慢指针
- linked-list-cycle-ii solution 第一次相遇 fast 和 slow 速度不同,相遇后 slow 退回 head,跑到再次相遇(此时快慢速度一样)
- intersection-of-two-linked-lists solution
- reverse-linked-list solution 递归实现反转单链表(模板), 需要背熟
- reverse-linked-list-ii solution python 的实现不太一样 需要背熟
- reverse-nodes-in-k-group solution 用迭代实现反转
- binary-search solution
- find-first-and-last-position-of-element-in-sorted-array solution
- search-insert-position solution
- remove-duplicates-from-sorted-array solution 原地修改数组 (快慢)
- remove-duplicates-from-sorted-list solution 原地修改链表 (快慢)
- remove-element solution 原地修改数组 (快慢)
- move-zeroes solution 原地修改数组 (快慢)
- two-sum-ii-input-array-is-sorted solution (两边向中间 move 的指针)
- reverse-string solution(两边向中间 move 的指针)
- longest-palindromic-substring solution(中间向两边 move 的指针)
- minimum-window-substring solution
- permutation-in-string solution
- find-all-anagrams-in-a-string solution
- longest-substring-without-repeating-characters solution
前缀和/积 rangeSum。 本质是用一个新数组 preSum 来存储元数组的累加和或者累加积,以使得算法的时间复杂度打到 O(1),when we creating the presum array, the length of row or column is always 1 bigger than the original one
- 对于 BST 的每一个节点 node,左子树节点的值都比 node 的值要小,右子树节点的值都比 node 的值大。
- 对于 BST 的每一个节点 node,它的左侧子树和右侧子树都是 BST。
- BST 中序遍历就是升序排序结果」这个性质,每次寻找第 k 小的元素都要中序遍历一次,最坏的时间复杂度是 O(N)
二叉搜索树_特性篇 下面三题都是中序
- kth-smallest-element-in-a-bst Solution travese 的思路
- convert-bst-to-greater-tree Solution travese 的思路
- binary-search-tree-to-greater-sum-tree Solution 和上一题一模一样
二叉搜索树_基操篇 判断 BST 的合法性、增、删、查。其中「删」和「判断合法性」略微复杂
- validate-binary-search-tree Solution 分解问题的思路,使用尾递归 返回值。None 的时候返回 True。注意参数的传递 很有意思。
- delete-node-in-a-bst Solution 当删除节点有两个子节点, A 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。最后需要返回 root
- search-in-a-binary-search-tree Solution
- insert-into-a-binary-search-tree Solution 最后也需要返回 root
- unique-binary-search-trees-ii Solution 结合 后序 二叉树(子问题的思路) 动态规划 memo 的 base case。子问题的思路
- 1 穷举 root 节点的所有可能。2、递归构造出左右子树的所有合法 BST。 3、给 root 节点穷举所有左右子树的组合。
- unique-binary-search-trees Solution 这一题的本质是特殊的动态规划 memorization(一开始我以为是回溯,但不是)
- binary-tree-preorder-traversal Solution
- diameter-of-binary-tree Solution 一个 root 的 diameter 是左边最深+右边最深 需要在 class 里定义一个 diameter
- maximum-depth-of-binary-tree Solution 找最深 在后序的位置用 max,尾递归
- flatten-binary-tree-to-linked-list Solution (分解问题)1、将 root 的左子树和右子树拉平。 2、将 root 的右子树接到左子树下方,然后将整个左子树作为右子树(虽然没有 return value 但仍然属于分解问题)
- populating-next-right-pointers-in-each-node Solution (遍历)这题用到完美二叉树,用 traverse 但是参数定义不一样,很有意思。同样执行转换的位置在前序或者后序都不影响
- invert-binary-tree Solution (遍历)这题的左右子树转换的代码位置在后序或者前序 并不影响结果(利用第一种遍历思路)
二叉树_构造 基本构造都用分解问题
- construct-binary-tree-from-preorder-and-inorder-traversal Solution 第二种思路 找到中序的 index,构造 build 函数,参数很多,第二次传参的中序 start 和 end 只和 index 有关 。一定要注意,传入的参数是 index!
- construct-binary-tree-from-inorder-and-postorder-traversal Solution 和上一题的思路一样
- maximum-binary-tree Solution 定义 build 函数 def build(nums,lo,hi):
- construct-binary-tree-from-preorder-and-postorder-traversal Solution 这一题可以有多种答案,利用 prestart 的后一个元素,所以需要多一个判断当 prestart=preend 的时候 直接 return TreeNode(preorder[prestart])
- construct-binary-search-tree-from-preorder-traversal Solution build(preorder,start,end) 用一个 while 循环找到第一个比 prestart 大的元素的 index
- serialize-and-deserialize-binary-tree Solution 1 递归解法绝对是 后序的大妙用
- Solution 2
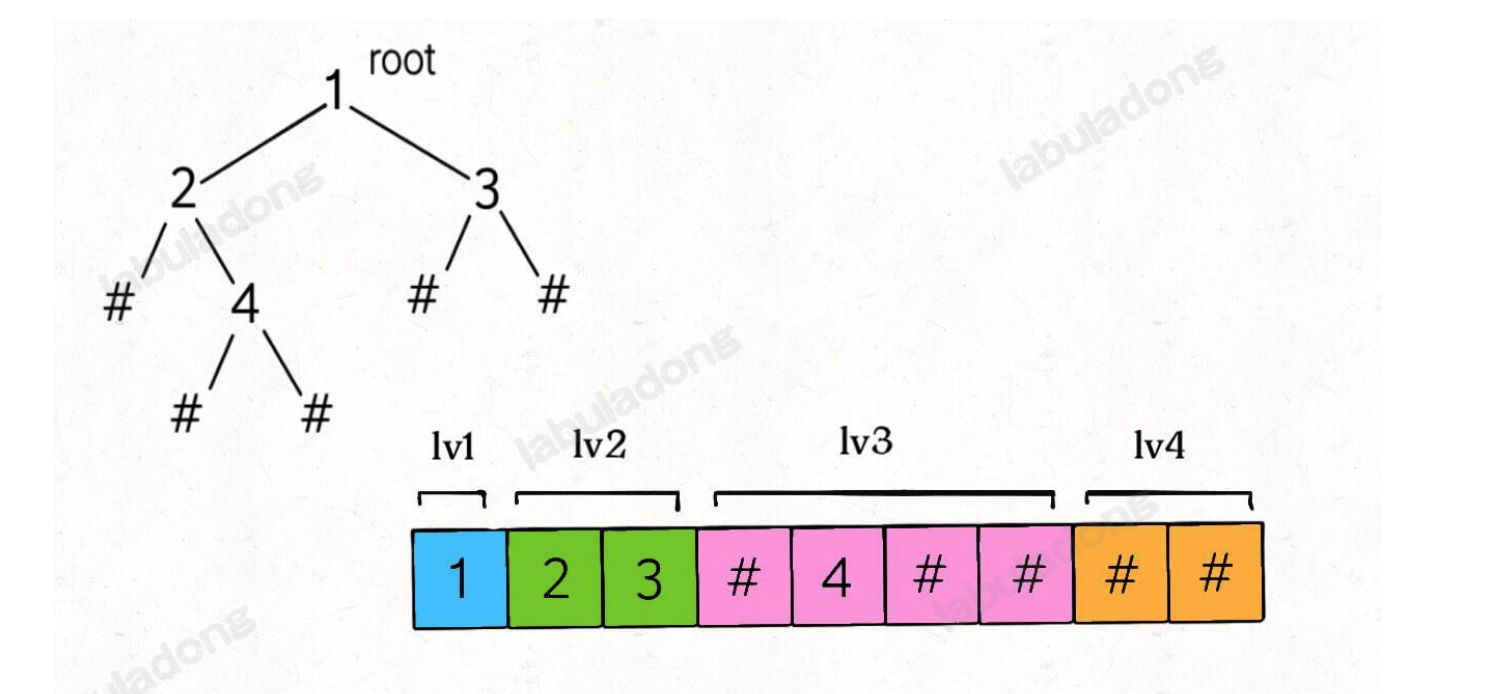
每一个非空节点都会对应两个子节点,那么反序列化的思路也是用队列进行层级遍历,同时用索引 i 记录对应子节点的位置:
- Template
- n-queens Solution
- permutations Solution 用了 printindent 的操作(这个套路很*,适用于所有递归)
- permutations Solution 无重复 不可复选
- subsets Solution 无重复 不可复选
- subsets-ii Solution 有重复 不可复选
- permutations-ii Solution 有重复 不可复选
- combinations Solution 无重复 不可复选
- combination-sum Solution 无重复 可复选
- combination-sum-ii Solution 可重复 不可复选
- combination-sum-iii Solution 这题我还没做
islands (岛屿 也就是 flood fill)
- a simple framework demo for island Solution
- number-of-islands Solution ### 最简单的 直接淹
- max-area-of-island Solution
- number-of-enclaves Solution
- number-of-closed-islands Solution
- count-sub-islands Solution
- number-of-distinct-islands Solution
- adjacency list depth first search template 简单邻接表图深度遍历的 python 实现模板
- all-paths-from-source-to-target solution 这一题是邻接表
- fibonacci-number Solution
- coin-change Solution memo Solution table
- longest-increasing-subsequence Solution 子序列问题,注意子序列 并不是连续的 for i in range(1,len(dp)): for j in range(0,i): 两个 for 循环 复杂度是 n 方
- russian-doll-envelopes Solution 这个的思路是先用 lambda 排序 在进行 LIS
- maximum-subarray Solution 这个是 subset 区别这个和 subsequence

