Box2d刚体轨迹预测

前言

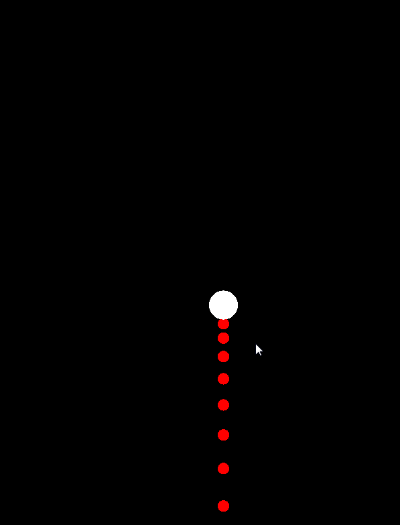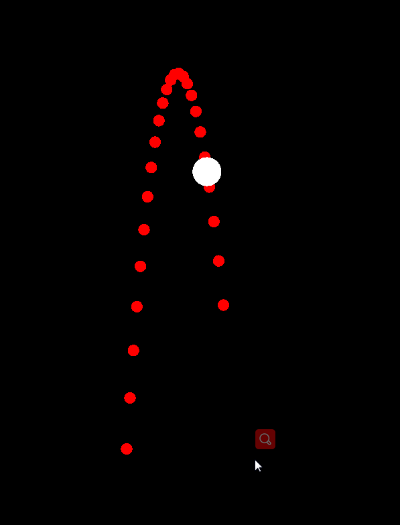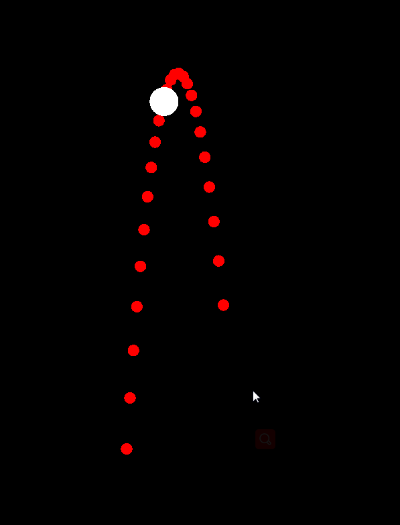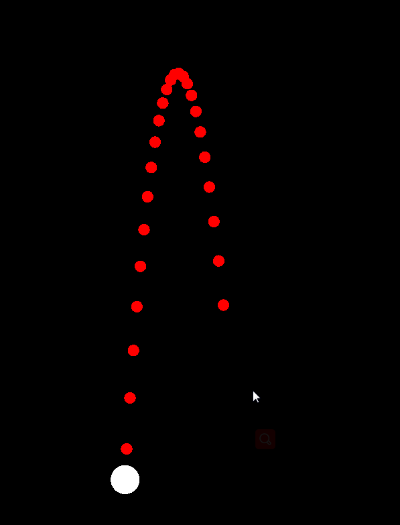
在游戏开发中经常会接触到各种物理引擎，虽然开源的引擎各种各样，但是基本原理是相通的。实质上物理引擎只是以时间为单位的刷新物理世界中的刚体的位置（其中运用了大量物理公式和知识），然后刷新刚体关联的物品（节点）的位置来达到模拟效果。其中的细节是我们开发者不需要知道，也不知道的。所以刚体轨迹预测成为了难题。

物理公式

在开始之前先补一下高中基础物理公式（主要涉及匀加速直线运动）：

速度公式 $v=v_0+at$
距离公式 $s=v_0t+\frac{1}{2}at^2$
阻尼公式 $v=v-kv_0t$ (比较贴近)

$v_0$是指运动物体的初始速度，$t$是指运动物体的运动时间，$v$是指运动物体的结束速度，$s$是指运动物体运动距离，$a$是指运动物体的运动加速度，$k$是指运动物体的阻尼系数(模拟的空气阻尼等)。

即：

	//速度公式
	v(v0, a, t) {
		return v0 + a * t;
	}
	//距离公式 
	s(v0, a, t) {
		return v0 * t + (a * t * t) / 2;
	}
	//阻尼公式
	let damping = -this.linear_Damping * this.v_y * dt;
	this.v_y = this.v(this.v_y, this.a_y, dt) + damping;

运动分解

运动比较复杂，但是可以简单的拆解为X轴运动和Y轴运动，把运动简单化。

Y轴

阻尼系数：

this.linear_Damping = this.RigidBody.linearDamping;

加速度为物理世界重力*刚体的重力缩放(PTM_RATIO为单位换算比)：

let world_y = cc.director.getPhysicsManager().gravity.y;
this.a_y =(-this.RigidBody.gravityScale * world_y) /cc.PhysicsManager.PTM_RATIO;

速度为物体初始速度(PTM_RATIO为单位换算比):

this.v_y =-this.RigidBody.linearVelocity.y / cc.PhysicsManager.PTM_RATIO;

刚体Y轴位置:

this.y = this.RigidBody.node.y;

经过dt时间，物体Y轴运动为(PTM_RATIO为单位换算比)：

this.y -= this.s(this.v_y, this.a_y, dt)*cc.PhysicsManager.PTM_RATIO;
let damping = -this.linear_Damping * this.v_y * dt;
this.v_y = this.v(this.v_y, this.a_y, dt) + damping;

X轴

同理...

关键代码

const { ccclass, property } = cc._decorator;

@ccclass
export default class RigidBodyaPrediction extends cc.Component {
	@property(cc.RigidBody)
	RigidBody: cc.RigidBody = null;

	@property(cc.Prefab)
	show_prefab: cc.Prefab = null;

	@property(cc.Node)
	result: cc.Node = null;
	
	//米/秒^2
	a_y = 0;
	a_x = 0;
	//米/秒
	v_y = 0;
	v_x = 0;
	//位置
	x = 0;
	y = 0;
	//阻尼
	linear_Damping = 0;

	status = true;

	pool: cc.Node[] = new Array<cc.Node>();

	onLoad() {
		for (let index = 0; index < 25; index++) {
			let tmp = cc.instantiate(this.show_prefab);
			this.pool.push(tmp);
			this.result.addChild(tmp);
		}
	}
	init() {
		let world_y = cc.director.getPhysicsManager().gravity.y;
		let world_x = cc.director.getPhysicsManager().gravity.x;
		this.a_y =
			(-this.RigidBody.gravityScale * world_y) /
			cc.PhysicsManager.PTM_RATIO;
		this.a_x =
			(this.RigidBody.gravityScale * world_x) /
			cc.PhysicsManager.PTM_RATIO;
		this.v_y =
			-this.RigidBody.linearVelocity.y / cc.PhysicsManager.PTM_RATIO;
		this.v_x =
			this.RigidBody.linearVelocity.x / cc.PhysicsManager.PTM_RATIO;
		this.x = this.RigidBody.node.x;
		this.y = this.RigidBody.node.y;
		this.linear_Damping = this.RigidBody.linearDamping;
	}
	start() {
		this.RigidBody.node.on(
			cc.Node.EventType.TOUCH_CANCEL,
			function() {
				this.RigidBody.type = cc.RigidBodyType.Dynamic;
				this.status = false;
			},
			this
		);
		this.RigidBody.node.on(
			cc.Node.EventType.TOUCH_MOVE,
			function(event: cc.Touch) {
				let vec2 = this.RigidBody.node.convertToNodeSpaceAR(
					event.getLocation()
				);
				this.RigidBody.linearVelocity = new cc.Vec2(
					-vec2.x,
					-vec2.y * 2
				);
			},
			this
		);
	}

	show() {
		this.init();
		this.node.removeChild(this.RigidBody.node, false);
		this.node.addChild(this.RigidBody.node, 9999);
		for (let index = 0; index < 25; index++) {
			let tmp = this.pool[index];
			tmp.x = this.x;
			tmp.y = this.y;
			this.updatePostion(0.15);
		}
	}
	updateX(dt) {
		this.x += this.s(this.v_x, this.a_x, dt) * cc.PhysicsManager.PTM_RATIO;
		let damping = -this.linear_Damping * this.v_x * dt;
		this.v_x = this.v(this.v_x, this.a_x, dt) + damping;
	}
	updateY(dt) {
		this.y -= this.s(this.v_y, this.a_y, dt) * cc.PhysicsManager.PTM_RATIO;
		let damping = -this.linear_Damping * this.v_y * dt;
		this.v_y = this.v(this.v_y, this.a_y, dt) + damping;
	}
	updatePostion(dt) {
		this.updateX(dt);
		this.updateY(dt);
	}

	v(v0, a, t) {
		return v0 + a * t;
	}
	s(v0, a, t) {
		return v0 * t + (a * t * t) / 2;
	}
	update() {
		if (this.status) {
			this.show();
		}
	}
}

例子

RigidBodyaPrediction

0x2CA/RigidBodyaPrediction

Box2d刚体轨迹预测

前言

物理公式

运动分解

关键代码

例子