/DL-PupilModel

Official implementation of a temporal pupil light response model proposed in the Scientific Reports article: "Deep learning-based pupil model predicts time and wavelength-dependent light responses"

Primary LanguageMATLABGNU General Public License v3.0GPL-3.0

Code Repository
Deep learning-based pupil model predicts time and wavelength dependent light responses

Published DOI GPL3

This repository provides the official implementation of a deep learning-based temporal pupil light response model proposed in the article "Deep learning-based pupil model predicts time and wavelength-dependent light responses" authored by Babak Zandi and Tran Quoc Khanh from the Technical University of Darmstadt.

[Paper] [Supplementary materials]

Pupil light response models aim to predict the pupil diameter in millimetres using a light spectrum or derived photometric quantities. State-of-the-art pupil models can only calculate a static diameter at an equilibrium state with the luminance as a main dependent parameter [1]. A recent work showed that such L- and M-cone based pupil models have prediction errors of up to 1.21 mm, mainly caused by the missing time dependence of current pupil functions and the lack of integrating the contribution of the intrinsically photosensitive ganglion cells [2].

We developed the first concept of a pupil model, which can predict the temporal pupil diameter up to 300 seconds for chromatic ( = 450 nm, = 530 nm, = 610 nm, = 660 nm) and polychromatic spectra (~2000 K, ~5000 K, ~10 000 K) at ~100 cd/m2. The differential equation of Fan & Yao [3] was combined with the Watson & Yellot model [1] and feed-forward neural networks to reconstruct the temporal pupil diameter caused by sustained light stimuli. For this, light metrics such as the luminance and a respective CIExy-2° chromaticity coordinate of a light stimulus are used as features to predict model parameters of a base-function. Next, the predicted model parameters can be fed into the basis-function, which finally describes the corresponding temporal pupil light response with a mean absolute error of less than 0.1 mm. Our approach is data-driven through the integration of neural networks. Compared to existing approaches, we can predict the pupil diameter's time course from light metrics for the first time. Furthermore, the modelling approach is flexible, allowing a continuous improvement of the model. Currently, the prediction space is limited, but the model quality can be enhanced with additional data due to the integration of neural networks. We are currently working on a pupil light response database to train the model for more light stimuli. Further details are explained in our publication [4]. In the future, it is conceivable that further input parameters will be added to the model in order to integrate cognitive parameters that could influence pupil diameter.

📧 Correspondence: zandi@lichttechnik.tu-darmstadt.de
Google Scholar Profile: Babak Zandi
Twitter: @BkZandi

Code Overview

This repository contains the neural network models in the folder Python/A03_Models/FF, which were trained with an intrasubject TrainData_Individual_Subject.csv and intersubject TrainData_Many_Subject.csv pupil light response dataset. The combined model itself is implemented as in the function NNCombinedModel.m using Mathworks Matlab. The function predicts the temporal pupil diameter from three different light metrics variants as input parameters:

  • Variant 1: Luminance, CIExy-2° coordinates.
  • Variant 2: α-opic radiance values of the L-cones , M-cones, S-cone and ipRGCs.
  • Variant 3: Luminance, CIExy-2°and melanopic radiance.

The neural networks can be trained optionally again with the individual input parameter variants using the Python/Main.py file with the argument --Variant which defines the model's input value combination. We already uploaded the trained models to this repository. Therefore we recommend this new training step only if you need to train your own models based on your custom datasets. The following command trains the neural network with the TrainData_Many_Subject.csv dataset using the respective hyperparameters from our article:

  • Variant 1: python Main.py --Variant 1
  • Variant 2: python Main.py --Variant 2
  • Variant 3: python Main.py --Variant 3

Before running the training command, you have to make the following new folders Python/A04_Results_Training/01_Plots/and Python/A04_Results_Training/02_Data/in which the training results will be logged. The checkpoint-models will be saved in the folder Python/A02_Models/FF. To train the model with the TrainData_Individual_Subject.csv dataset you need to change the line pd.read_csv('A00_Data/TrainData_Many_Subject.csv') to pd.read_csv('A00_Data/TrainData_Individual_Subject.csv') in the file Python/A01_Functions/ReadData.py. The programming code of the neural networks can be found in Python/A02_Networks/FeedForward.py.

Dependencies

For implementing the neural networks, we have used PyTorch with the amazing pytorch_lightning framework. The demo code in this repository requires Python 3, PyTorch 1.4+, PyTorch Lightning 0.7+, Numpy, Pandas and Mathworks Matlab.

Implemented Model Structure

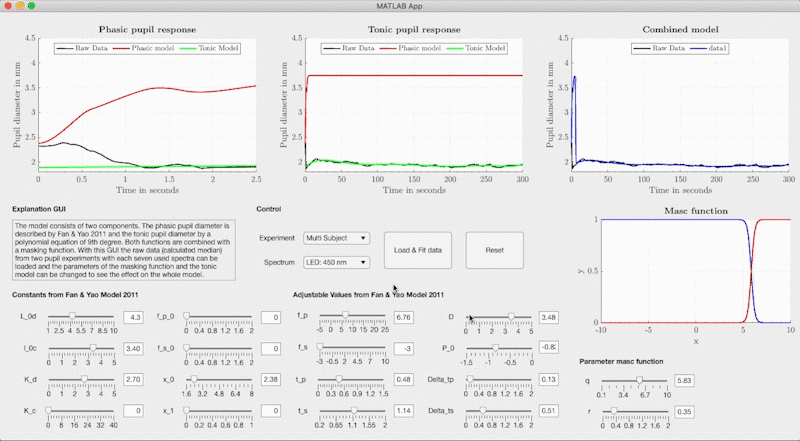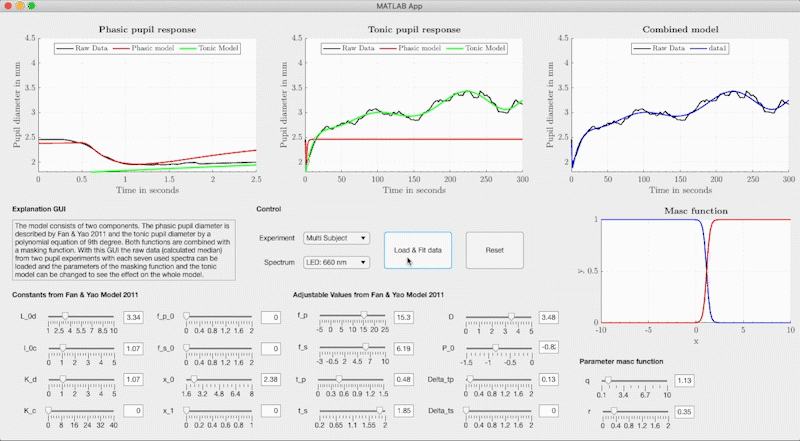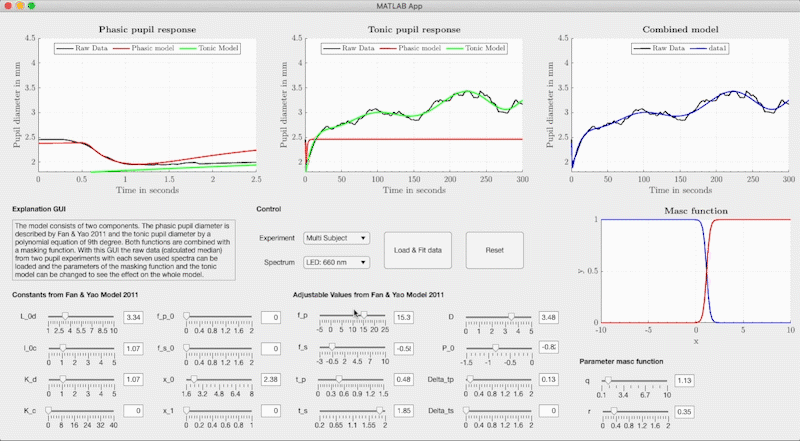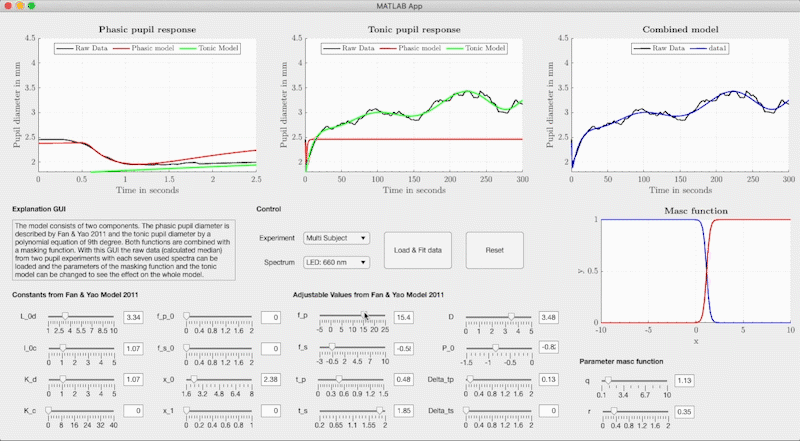
The combined model is structured so that the neural networks determine the respective model parameters of the base-function from light metrics with Variant 1, Variant 2 or Variant 3 (see Figure). The model parameters are used in Fan & Yao's differential equation for the phasic pupil diameter and in a polynomial equation to describe the tonic response. We use the Watson & Yellot model to calculate the pupil's starting point with which the solution of the differential equation is calculated with an ode45 solver. In the Watson & Yellot model, the adaptation stimulus' luminance should be used, which is usually presented in pupil light response investigations before the main stimulus. Finally, the phasic and tonic pupil response is combined with two masking functions, resulting in the reconstructed temporal pupil diameter.

The function for predicting the model parameters from the light metrics is implemented in the Python file Python/CalcParam.py. The function has the following arguments:

  • --Condition: Definition of which neural networks should be used to predict the base-function's model parameters. The condition Single employs the neural networks which were trained with the intrasubject data TrainData_Individual_Subject.csv. The value Multi uses the neural networks which were trained with the intersubject data TrainData_Many_Subject.csv.
  • --Variant: The number of the used input variant.

The respective light metrics need to be defined as additional arguments, which differ depending on the Variant. Thus, the following calls with double values are possible:

Variant 1 (Luminance L, CIExy-2° chromaticity coordinates Fx and Fx)

python CalcParam.py --Condition Single --Variant 1 --L doubleValue --Fx doubleValue --Fy doubleValue

Variant 2 (α-opic radiance values of the L-cones Lcone , M-cones Mcone, S-cone Scone and ipRGCs Mel)

python CalcParam.py --Condition Single --Variant 2 --Lcone doubleValue --Mcone doubleValue --Scone doubleValue --Mel doubleValue`

Variant 3: (Luminance L, CIExy-2° chromaticity coordinates Fx and Fy)

python CalcParam.py --Condition Single --Variant 3 --L doubleValue --Fx doubleValue --Fy doubleValue --Mel doubleValue

After the calling CalcParam.py, the model parameters are saved in the file Python/output.csv. Note that the values double must be given normalised. The normalisation is already done in the file Functions/NNCombinedModel.m. We recommend calling the entire model from Matlab, as it is described in the section Getting Started.

Getting Started

The combined model can be run via the Matlab script Functions/NNCombinedModel.m. Before the script can be used, a valid path to your Python executable must be provided since the function Python/CalcParam.py is called from the Matlab environment. For this, change this line of code python_path = '/Users/papillon/opt/anaconda3/envs/ML/bin/python3';, which is located in the Functions/NNCombinedModel.m file in line 4. Demo codes of how to call the function for the different stimulus values are available in the Main.m file. Note, that the input parameters are restricted to those used in the Main.m file, as the model is currently not at a state for predicting model parameters beyond the training data. For instance, to predict the pupil light response from the single observer caused by LED spectra with a peak wavelength of 450 nm, 530 nm, 610 nm, 660 nm, 2000 K, 5000 K and 10000 K, you can use the following code snippet in Mathworks Matlab:

% Set the plot preferences (optional)
set(groot, 'DefaultLineLineWidth', 1);
set(groot, 'DefaultAxesLineWidth', 1);
set(groot, 'DefaultAxesFontName', 'CMU Serif');
set(groot, 'DefaultAxesFontSize', 14);
set(groot, 'DefaultAxesFontWeight', 'normal');
set(groot, 'DefaultAxesXMinorTick', 'on');
set(groot, 'DefaultAxesXGrid', 'on');
set(groot, 'DefaultAxesYGrid', 'on');
set(groot, 'DefaultAxesGridLineStyle', ':');
set(groot, 'DefaultAxesUnits', 'normalized');
set(groot, 'DefaultAxesOuterPosition',[0, 0, 1, 1]);
set(groot, 'DefaultFigureUnits', 'inches');
set(groot, 'DefaultFigurePaperPositionMode', 'manual');
set(groot, 'DefaultFigurePosition', [0.1, 11, 8.5, 4.5]);
set(groot, 'DefaultFigurePaperUnits', 'inches');
set(groot, 'DefaultFigurePaperPosition', [0.1, 11, 8.5, 4.5]);

% 0. Load data, add all essential folder to path
clc; clear; load("Data");

addpath("Data");
addpath("Functions");
addpath("Python");

% 1. Predict & Plot PLR from model with neural network - Single subject (Variant 1): L, CIExy-2°
% Light conditions in each col: '450nm'; '530nm'; '610nm'; '660nm'; '2000K'; '5000K'; '10000K'
Luminance = [99.73; 100.12; 100.16; 99.97; 100.17; 100.10; 99.83];
CIE_x = [0.15811; 0.18661; 0.67903; 0.71701; 0.53305; 0.34538; 0.28549];
CIE_y = [0.02006; 0.73928; 0.32039; 0.27995; 0.42288; 0.34976; 0.2769];

hparam.Condition = 'Single';
hparam.Variant = 1;

% Light conditino #1
Index = 1;
hparam.Stimuli = [Luminance(Index), CIE_x(Index), CIE_y(Index)];
[out, Predicted1] = NNCombinedModel(hparam);

% Light conditino #2
Index = 2;
hparam.Stimuli = [Luminance(Index), CIE_x(Index), CIE_y(Index)];
[out, Predicted2] = NNCombinedModel(hparam);

% Light conditino #3
Index = 3;
hparam.Stimuli = [Luminance(Index), CIE_x(Index), CIE_y(Index)];
[out, Predicted3] = NNCombinedModel(hparam);

% Light conditino #4
Index = 4;
hparam.Stimuli = [Luminance(Index), CIE_x(Index), CIE_y(Index)];
[out, Predicted4] = NNCombinedModel(hparam);

% Light conditino #5
Index = 5;
hparam.Stimuli = [Luminance(Index), CIE_x(Index), CIE_y(Index)];
[out, Predicted5] = NNCombinedModel(hparam);

% Light conditino #6
Index = 6;
hparam.Stimuli = [Luminance(Index), CIE_x(Index), CIE_y(Index)];
[out, Predicted6] = NNCombinedModel(hparam);

% Light conditino #7
Index = 7;
hparam.Stimuli = [Luminance(Index), CIE_x(Index), CIE_y(Index)];
[out, Predicted7] = NNCombinedModel(hparam);

% Plot predicted PLR against measured PLR
figure;
t = tiledlayout(3,3, 'Padding',"none", "TileSpacing","normal");
set(gcf, 'Position', [0.1, 11, 14, 8]);
t.Padding = "none";
t.TileSpacing = "compact";
LinewidthModel = 1;

ax1 = nexttile;
plot(linspace(0, 300, 30001)', Pupillendaten_Wide_OneSubject.Spektrum450nm.Median, 'k'); hold on;
plot(Predicted1.Time, Predicted1.CombinedModel, 'b', 'LineWidth', LinewidthModel);
xlabel('Time in seconds'); ylabel('PD in mm'); title({'Intrasubject (450 nm)' 'L, CIExy 2°'})
legend({'Measured PD', 'Predicted PD'},'Location','northwest','NumColumns', 2)

ax2 = nexttile;
plot(linspace(0, 300, 30001)', Pupillendaten_Wide_OneSubject.Spektrum530nm.Median, 'k'); hold on;
plot(Predicted2.Time, Predicted2.CombinedModel, 'b', 'LineWidth', LinewidthModel);
xlabel('Time in seconds'); ylabel('PD in mm'); title({'Intrasubject (530 nm)' 'L, CIExy 2°'})

ax3 = nexttile;
plot(linspace(0, 300, 30001)', Pupillendaten_Wide_OneSubject.Spektrum610nm.Median, 'k'); hold on;
plot(Predicted3.Time, Predicted3.CombinedModel, 'b', 'LineWidth', LinewidthModel);
xlabel('Time in seconds'); ylabel('PD in mm'); title({'Intrasubject (610 nm)' 'L, CIExy 2°'})

ax4 = nexttile;
plot(linspace(0, 300, 30001)', Pupillendaten_Wide_OneSubject.Spektrum660nm.Median, 'k'); hold on;
plot(Predicted4.Time, Predicted4.CombinedModel, 'b', 'LineWidth', LinewidthModel);
xlabel('Time in seconds'); ylabel('PD in mm'); title({'Intrasubject (660 nm)' 'L, CIExy 2°'})

ax5 = nexttile;
plot(linspace(0, 300, 30001)', Pupillendaten_Wide_OneSubject.CCT2000K.Median, 'k'); hold on;
plot(Predicted5.Time, Predicted5.CombinedModel, 'b', 'LineWidth', LinewidthModel);
xlabel('Time in seconds'); ylabel('PD in mm'); title({'Intrasubject (2000 K)' 'L, CIExy 2°'})

ax6 = nexttile;
plot(linspace(0, 300, 30001)', Pupillendaten_Wide_OneSubject.CCT5000K.Median, 'k'); hold on;
plot(Predicted6.Time, Predicted6.CombinedModel, 'b', 'LineWidth', LinewidthModel);
xlabel('Time in seconds'); ylabel('PD in mm'); title({'Intrasubject (5000 K)' 'L, CIExy 2°'})

ax7 = nexttile;
plot(linspace(0, 300, 30001)', Pupillendaten_Wide_OneSubject.CCT10000K.Median, 'k'); hold on;
plot(Predicted7.Time, Predicted7.CombinedModel, 'b', 'LineWidth', LinewidthModel);
xlabel('Time in seconds'); ylabel('PD in mm'); title({'Intrasubject (10 000 K)' 'L, CIExy 2°'})

set(ax1, 'YLim', [1, 5], 'XLim', [0, 300]); grid(ax1, 'off');
set(ax2, 'YLim', [1, 5], 'XLim', [0, 300]); grid(ax1, 'off');
set(ax3, 'YLim', [1, 5], 'XLim', [0, 300]); grid(ax1, 'off');
set(ax4, 'YLim', [1, 5], 'XLim', [0, 300]); grid(ax1, 'off');
set(ax5, 'YLim', [1, 5], 'XLim', [0, 300]); grid(ax1, 'off');
set(ax6, 'YLim', [1, 5], 'XLim', [0, 300]); grid(ax1, 'off');
set(ax7, 'YLim', [1, 5], 'XLim', [0, 300]); grid(ax1, 'off');

In addition to the combined model, we provide a graphical user interface that can adjust the base function's model parameters freely without the neural networks. We used the GUI to fit the base function to our measured pupil data and to create the training data for the neural networks. The GUI can be started via the file GUI/PupilModel_FittingParam.mlapp from Matlab. In the GUI, the measured pupil data for the respective light stimuli are stored and the model parameters can be freely adjusted.

Miscellaneous

For the interested readership, we highly recommend to check out the Matlab implementation of the time-independent classical L- and M-cone based pupil models. The models were implemented by William Wheatley & Manuel Spitschan based on the publication from Watson & Yellot [1]:

https://github.com/spitschan/WatsonYellott2012_PupilSize

An analysis of the prediction errors of such classical L- and M-cone based pupil models was performed in the following publication:

Zandi, B., Klabes, J. & Khanh, T.Q. Prediction accuracy of L- and M-cone based human pupil light models. Sci Rep 10, 10988 (2020). https://doi.org/10.1038/s41598-020-67593-3

Citation

Please consider to cite our work if you find this repository or our results useful for your research:

Zandi, B., Khanh, T.Q. Deep learning-based pupil model predicts time and spectral dependent light responses. Sci Rep 11, 841 (2021). https://doi.org/10.1038/s41598-020-79908-5

@article{Zandi2021,
author = {Zandi, Babak and Khanh, Tran Quoc},
doi = {10.1038/s41598-020-79908-5},
issn = {2045-2322},
journal = {Scientific Reports},
number = {1},
pages = {841},
title = {{Deep learning-based pupil model predicts time and spectral dependent light responses}},
url = {https://doi.org/10.1038/s41598-020-79908-5},
volume = {11},
year = {2021}}

References & Sources

[1]: Watson, A. B. & Yellott, J. I. A unified formula for light-adapted pupil size. J. Vis. 12, 1–16 (2012).

[2]: Zandi, B., Klabes, J. & Khanh, T.Q. Prediction accuracy of L- and M-cone based human pupil light models. Sci Rep 10, 10988 (2020). https://doi.org/10.1038/s41598-020-67593-3

[3]: Xiaofei Fan & Gang Yao. Modeling Transient Pupillary Light Reflex Induced by a Short Light Flash. IEEE Trans. Biomed. Eng. 58, 36–42 (2011).

[4]: Zandi, B., Khanh, T.Q. Deep learning-based pupil model predicts time and spectral dependent light responses. Sci Rep 11, 841 (2021). https://doi.org/10.1038/s41598-020-79908-5

License

This work is licensed under a Creative Commons Attribution 4.0 International License. The code is licensed under GPL3.