gros is a python package to numerically calculate and simulate particle trajectories based on the field equations of general relativity. A user needs to define a certain metric by providing the mass of a central gravitational attractor and the start coordinates and velocity of the test particle.
Clone the repository from https://github.com/BjoB/gros. After this you can install the package via pip in your choosen environment:
pip install .To simulate particle trajectories around a spherically symmetric body, we use the Schwarzschild solution of Einstein's field equations, describing the exterior spacetime for our use case. Starting from the field equations
with a vanishing energy momentum tensor
the Schwarzschild metric can be derived as
with the Schwarzschild radius
The intrinsic space time curvature can be derived from the metric by evaluating the Christoffel symbols given with
After calculating these coefficients and using the proper time as parameter, the motion of of a particle in the gravitational field can be retrieved by solving the system of differential equations given with the geodesic equations
Some simple simulations can be found in the examples directory.
This example simulates a particle orbiting the sun with some initial orbital parameters taken from https://nssdc.gsfc.nasa.gov/planetary/factsheet/. After calculating the trajectory, an animation will be generated, which can be used to track the particle with a previously choosen step size.
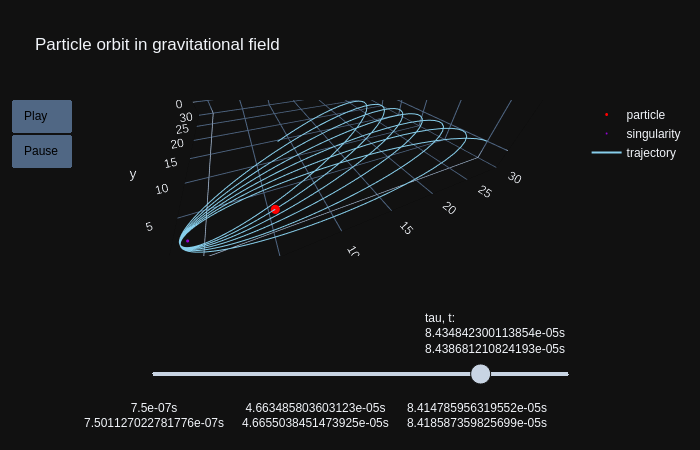
What if earth was a black hole? The according example shows how a particle would act in short distance of 30m. Especially the perihelion precession is visualized as a direct effect of general relativity. Additionally the gravitational time dilation can be tracked along the animation frames with τ as the proper time of the particle. t is the calculated coordinate time, which can be seen as the measured proper time of a hypothetical observer positioned infinitely far away from the gravitational center.