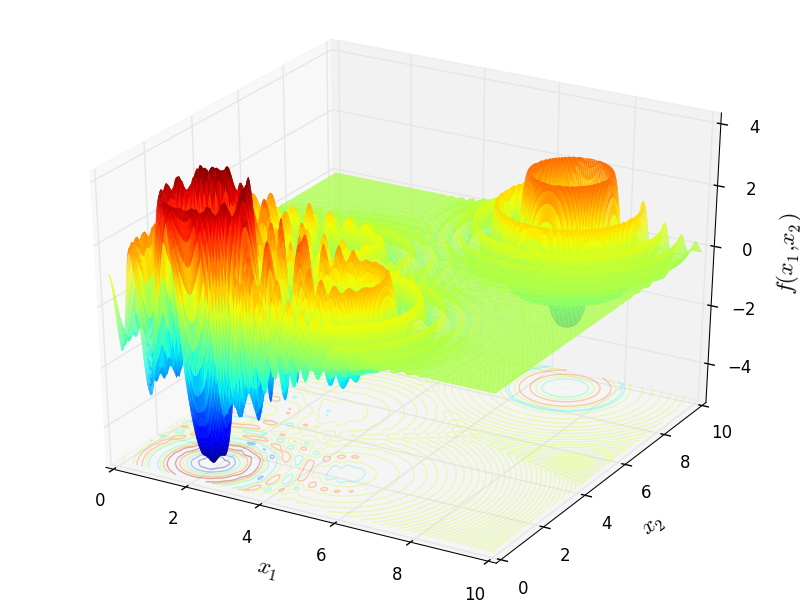
Genetic Algorithm Academic C++ Project
The goal of this program is to use the principle of genetic algorithms to obtain an optimal solution to a certain function. For this demonstration, the Langermann function and a random polynomial function were used to prove the efficiency of the program. First, a population of X random individuals was created. Then, their fitness was evaluated. The fitness is the individual's “survival chance”. In both cases, lower was better. This initial population becomes the current parent pool. Then, an offspring pool of 10 times the initial population size (X) is created through the mutation and crossover of multiple randomly selected parents. Both parent pool and offspring pool are merged into a joint pool and sorted by fitness. The first X individuals of the joint pool are the new parent pool and the process is done over and over again for as long as it is needed. The loop will only end if the termination criteria is fulfilled. Either it is a fixed number of generations or until an individual attains a certain desired fitness. The final product should find the minimal point of the Langermann function and the A,B,C and D of the cubic polynomial function through multiple iterations.
The Langermann Function