Controle Quântico Ótimo

Procedimentos iniciais

Para o seguinte trabalho utilizou-se da plataforma jupyter com o objetivo de exibir as atividades em python. Para tal, usou-se a jupyter-notebook na sua versão 7 com o python na sua versão 3.11.4. Para que o código do repositório execute normalmente é necessário a instalação das bibliotecas abaixo.

pip install numpy scipy matplotlib jupyter sympy

Como estudante de engenharia de computação, se torna importante estudar os diferentes métodos de controle existentes no mercado e, através desse tópico, incentiva-se a pesquisa ao redor do controle de partículas com o uso do Modelo Preditivo de Controle. Esse projeto se trata de uma interdisciplinariedade entre os cursos de engenharia de computação, engenharia elétrica, física e matemática. Com o advento dessa pesquisa, projeta-se a instauração das disciplinas de Introdução a Computação Quântica e Introdução a Modelagem Matemática.

Sumário

Atividade 1 - Comportamento da onda
Atividade 2 - Aproximação das derivadas
Atividade 3 - Realização do projeto de controle
Atividade 4 - Preparação dos estados quânticos
Atividade 5 - MPC para sistemas quânticos abertos

Atividade 1 - Comportamento da onda

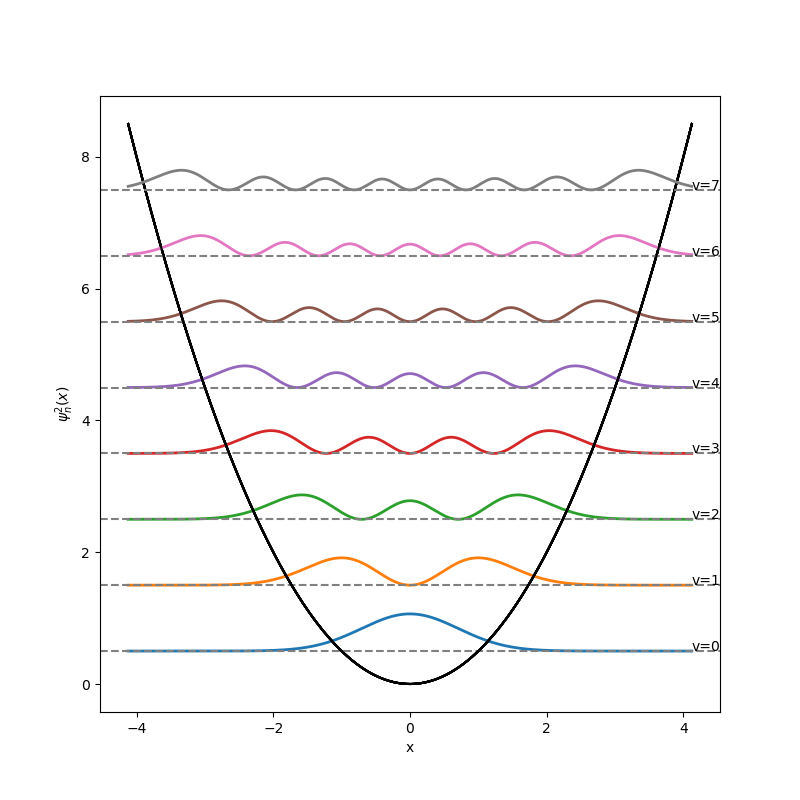
Nessa atividade estudaremos a representação de sistemas quânticos por meio da equação de Schrödinger, apresentada abaixo, e sua solução para o caso do oscilador harmônico simples.

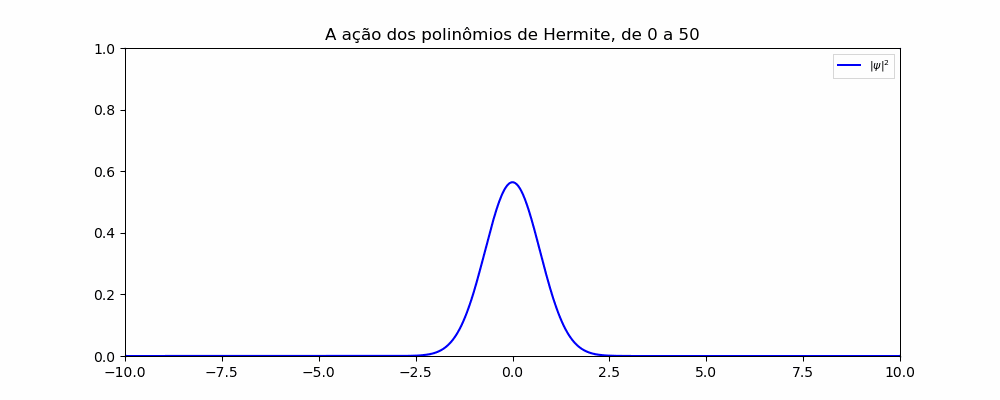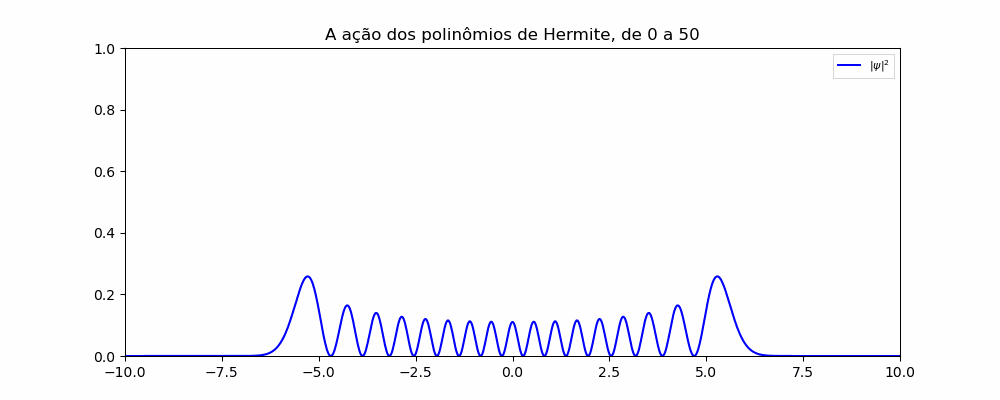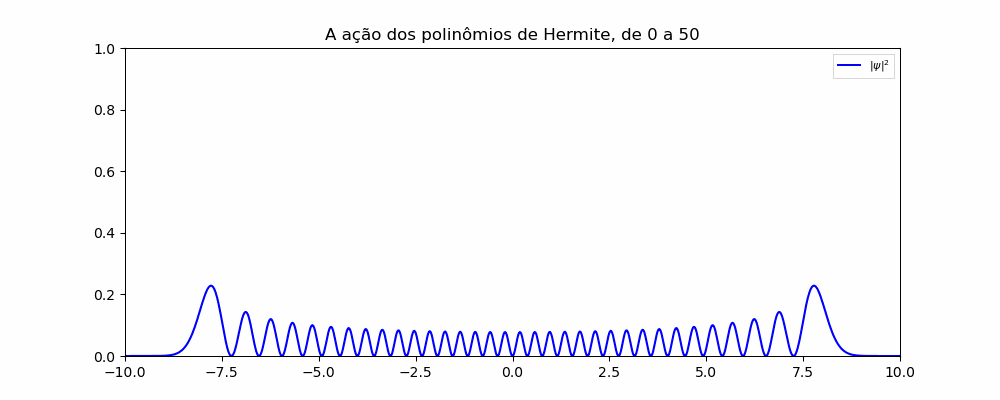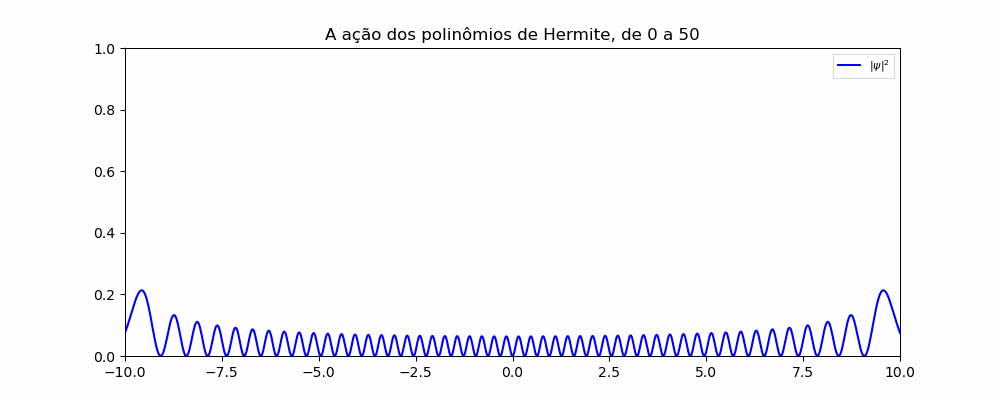
$$i\hbar\cdot\frac{\partial\psi}{\partial t} = \frac{\hbar^{2}}{2m}\cdot\frac{\partial^{2}\psi}{\partial x^{2}}+V(x,t)\psi(x,t)$$

A solução apresentada no artigo do Dr. Hashimoto é para o sistema do poço quadrado infinito e é suficiente para entender o processo de discretização e obtenção do resultado. Utilizando o livro base da Mecânica Quântica, por David Griffiths, usaremos a resposta para o oscilador harmônico juntamente dos polinômios de Hermite para modelar sua reposta analítica e usar o artigo para discretizar para o sistema OHS, portanto:

$$V(x) = 0.5mw^{2}x^{2}$$

$$\psi_n(x) = \left(\frac{m\omega}{\pi\hbar}\right)^{1/4}\cdot H_n(x)\cdot \frac{1}{\sqrt{2^nn!}}e^{0.5x^2}$$

Para a modelagem da parte analítca utilizou-se os seguintes parâmetros: $\omega = \pi$, $\hbar = 1$ e $m = 1$.

Resultados no espaço

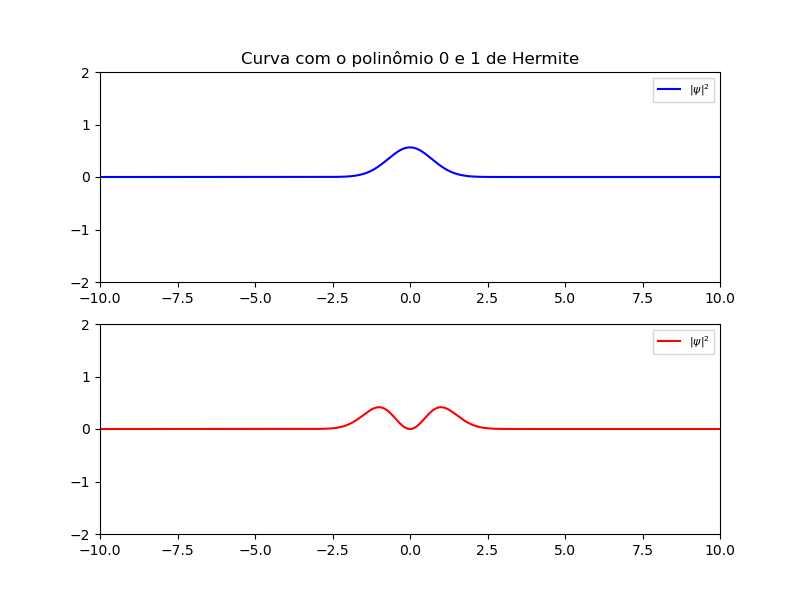
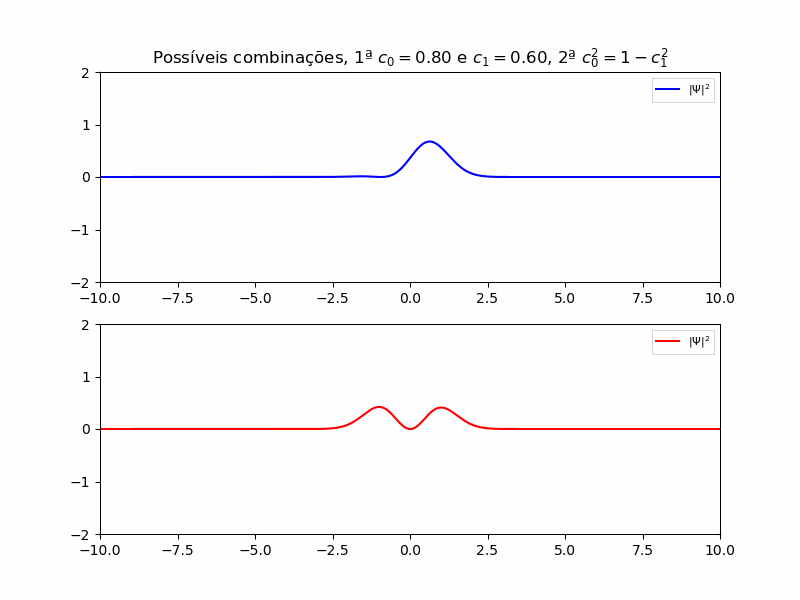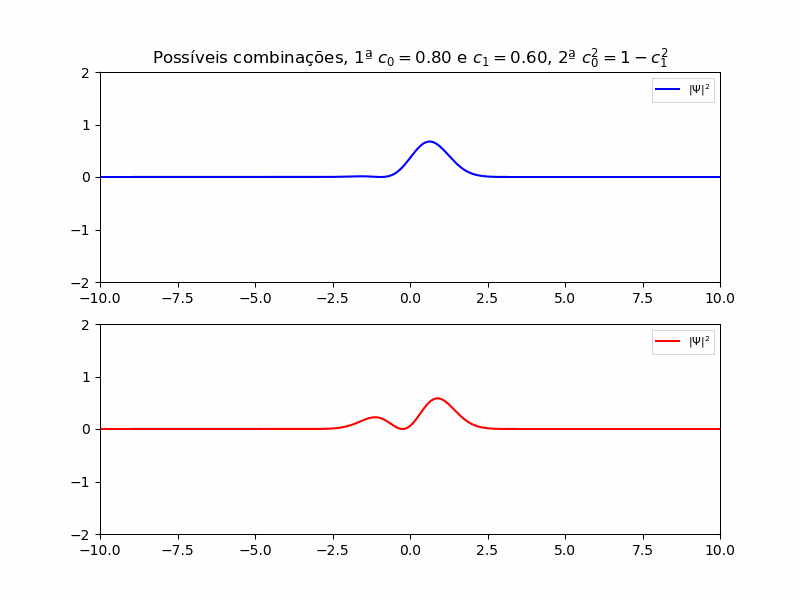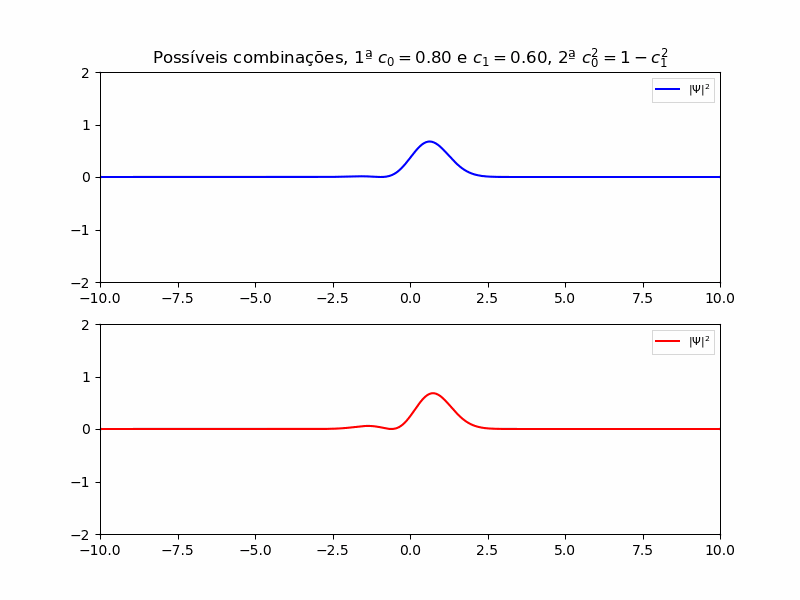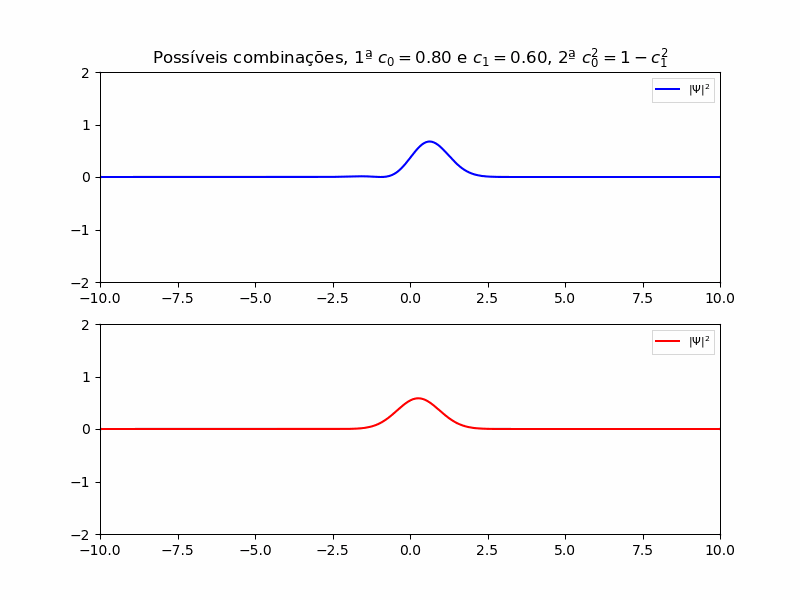
De acordo com a teoria proposta para a equação de Schrödinger, a solução para a equação pode ser determinada pela combinação linear de cada $\psi_n(x)$ para todo n pertencente aos naturais. Neste trabalho combinaremos a respostas em 0 e 1 com o valor constante de 0.80 e 0.60 suficiente para que a soma de seus quadrados dê 1. Abaixo estão as curvas com o polinômios de Hermite para graus maiores que 1.

E a combinação está representada abaixo:

A resposta com a combinação de 0 e 1 se torna importante pois se trata de um sistema de dois níveis, este que é muito importante para os estudos de mecânica quântica pois a maioria dos sitemas podem ser interpretados como um sistema de dois níveis, já que se trata de uma passagem de um estado ao outro.

Resultados no espaço-tempo

Para concretizar e observar o resultado analítico devemos multiplicar por $e^{-i(n+1/2)\omega t}$ ambos os $\psi$'s, dessa forma obtendo uma oscilação (Griffiths, David. 2011).

Atividade 2 - Aproximação das derivadas

Para a segunda atividade foi necessário entender de que forma poderia se aproximar as derivadas para facilitar a sua utilização em laboratórios de controle. Para realizar essa tarefa, utilizou-se a aproximação de derivadas pelo método de Crank-Nicolson do qual está demonstrado em um arquivo pdf nesse repositório. Nesse método, ocorre uma aproximação por diferenças, especificamente uma média entre a aproximação posterior e anterior de um ponto relacionado. Abaixo está um gráfico comparativo, entre o método de aproximação e a referência, além da representação dos erros absolutos e relativos.

Vale ressaltar que os erros dos quais realizam uma comparação com zero apresentam uma tendência a ir ao infinito devido a sua divisão, no entanto, isso não invalida a aproximação.

Atividade 3 - Realização do projeto de controle

Para essa etapa vamos arbitrar um valor para o potencial de forma que ele seja capaz de transformar a resposta sem alterar as constantes que o regem. Perceba que isso é um teste que utilizará o método MPC de modo a minimizar os erros entre a curva atual e a ideal no fim realizando uma acumulação.

$$V(x,t) = 1/2mwx^2 + u(t)$$

E o objetivo é:

$$ \Psi(x,t) = 0.80 \psi_0(x)e^{-iwt/2}+0.60\psi_1(x)e^{-3iwt/2} -> MPC -> \Psi_d(x,t)=1/\sqrt 2(\psi_0(x)e^{-iwt/2}+\psi_1(x)e^{-3iwt/2}) $$

De modo que a seguinte operação resulte no menor valor possível:

$$E = \sum_{n = p}^{p+N_h}||\Psi_d(x,t) - \Psi_{i}^n(u, x,t)||^{2}$$

A cada iteração, descobriremos qual é o melhor valor para u por meio de uma otimização não linear regida pela restrição da equação de Schrödinger. P, indicado pelo somatório é o ponto de partida do horizonte analisável. Para a primeira etapa seguiremos com o horizonte de tamanho 3, dessa forma, p começa em 0 e irá até 2 e na próxima iteração, começaremos em 1 até 3, sempre acumulando o resultado anterior para o caso de $\psi$.

É uma análise custosa por causa da matriz 1000x1000 utilizada, já que estamos usando a resposta analítica e essa depende do espaço de x que é $R^{2}$. Para isso, fora realizado testes com matrizes de 100x100 até 500x500, sendo de 100x100 até 400x400 utilizando o método de otimização gradiente e a matriz 500x500 utilizou-se a otimização da biblioteca sympy com o método SLSQP.

Com gradiente:

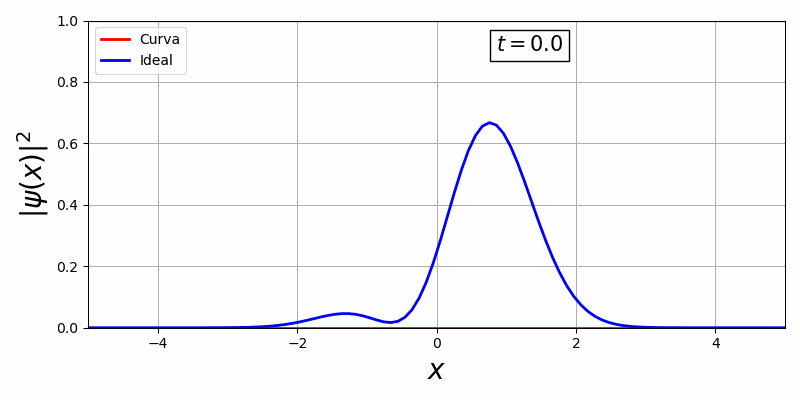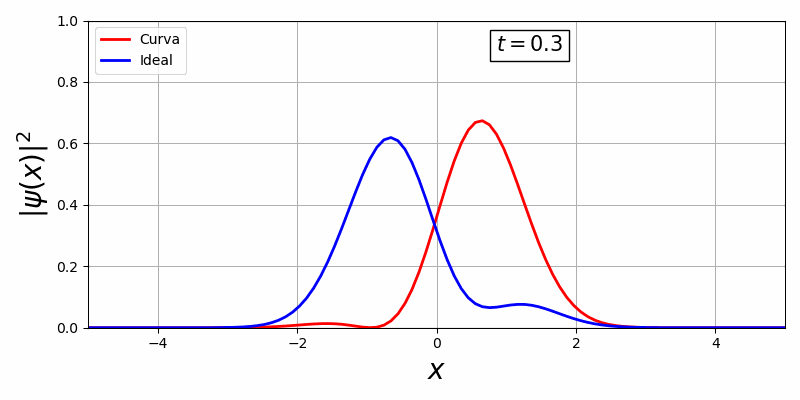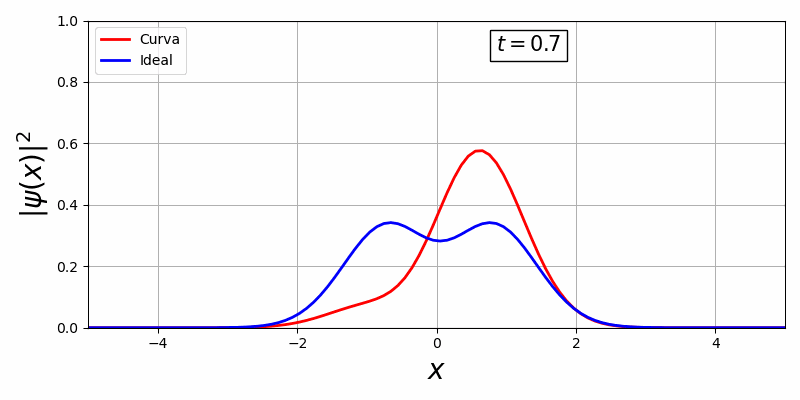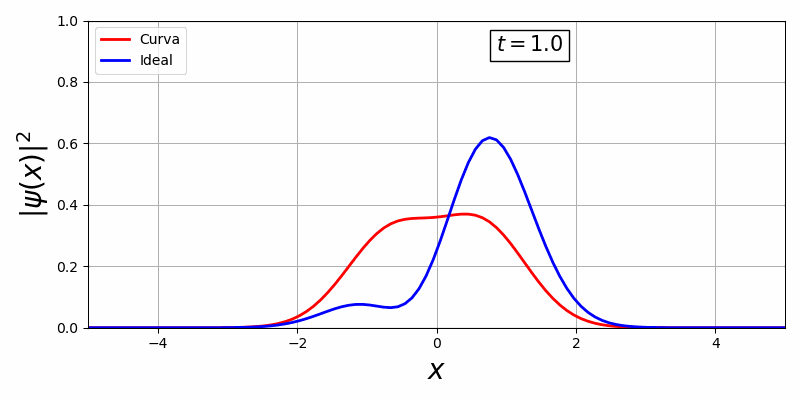
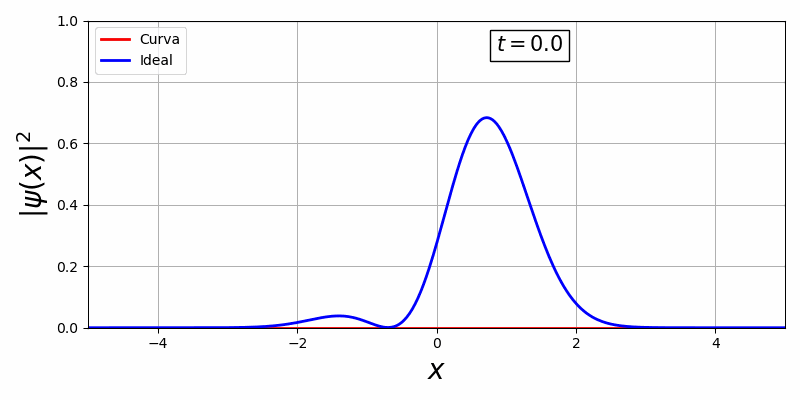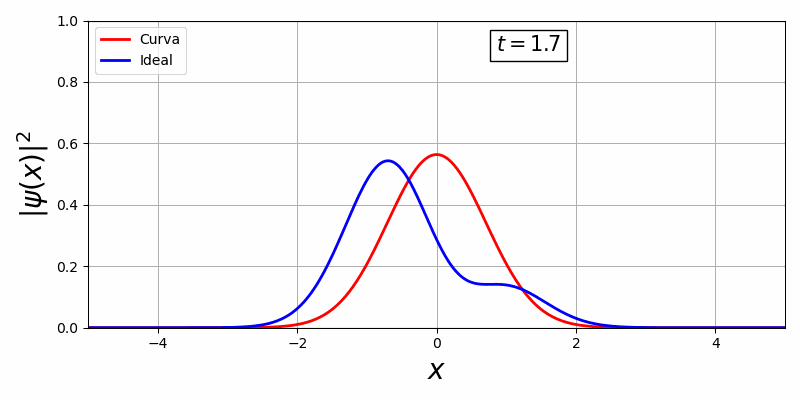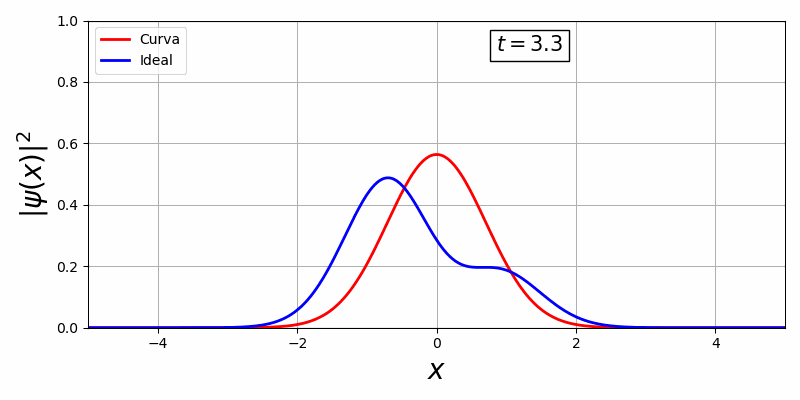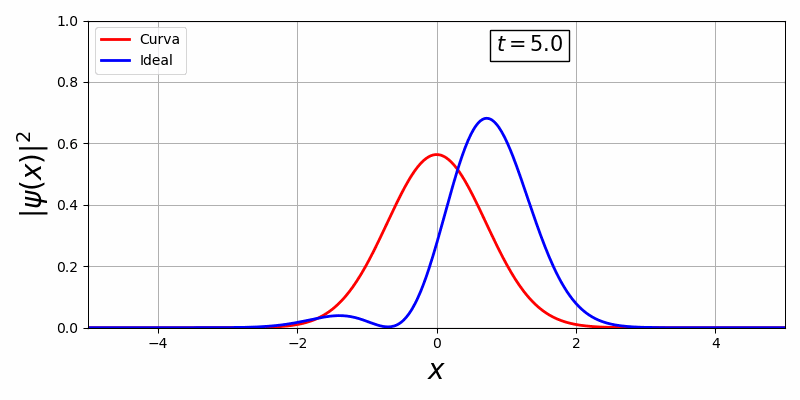
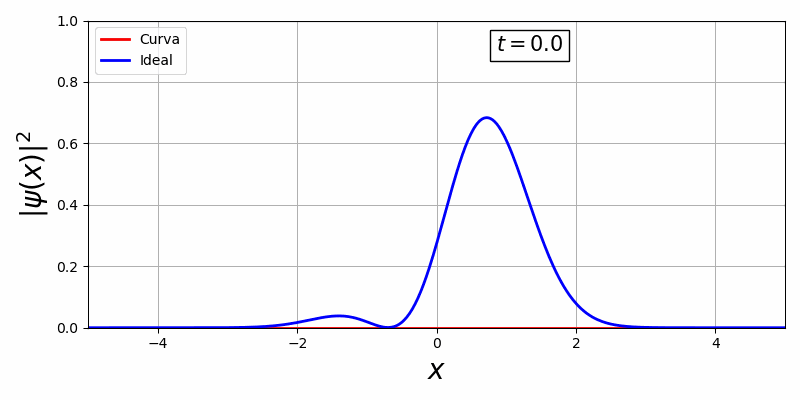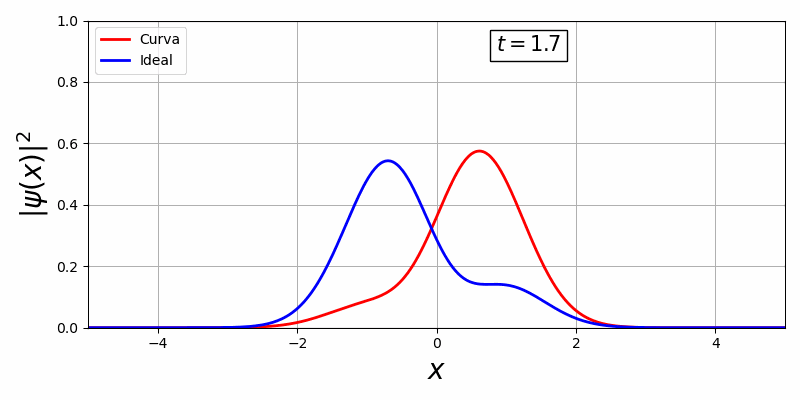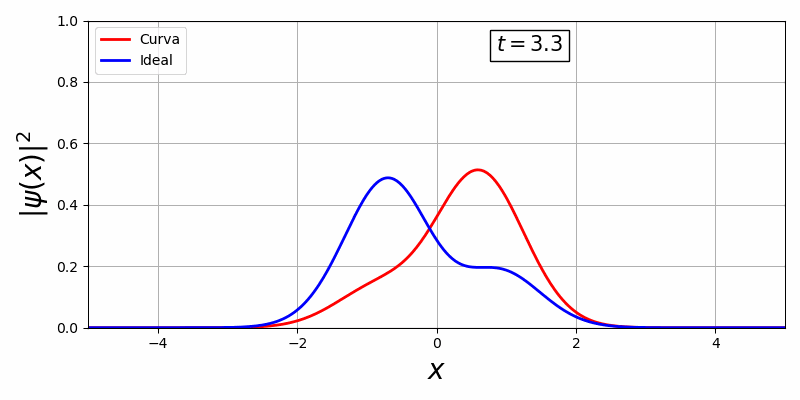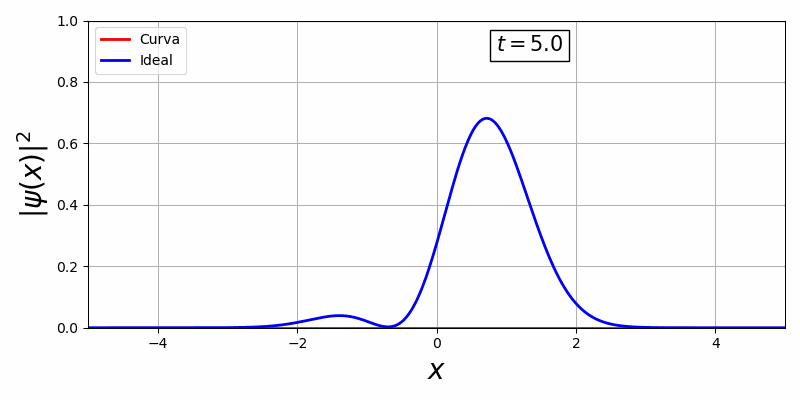
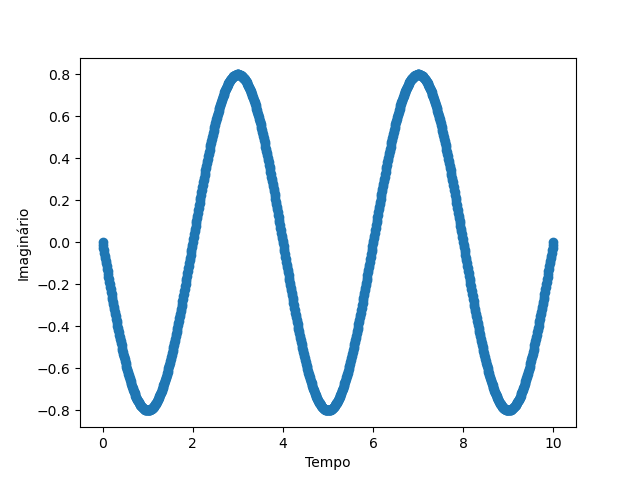
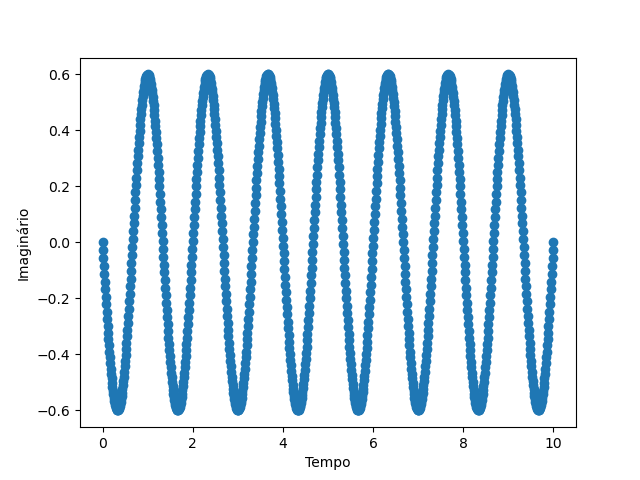
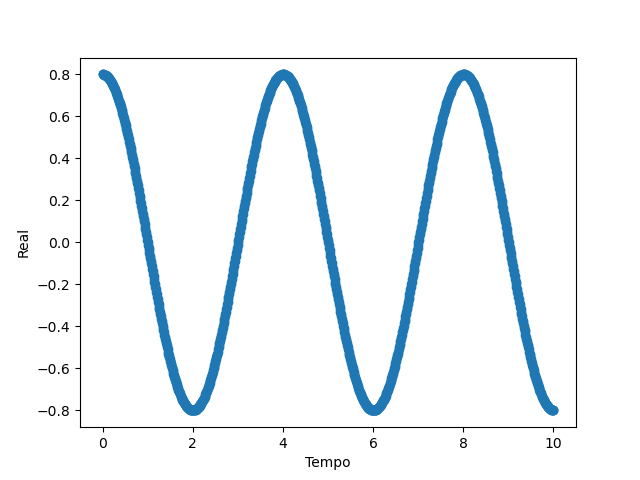
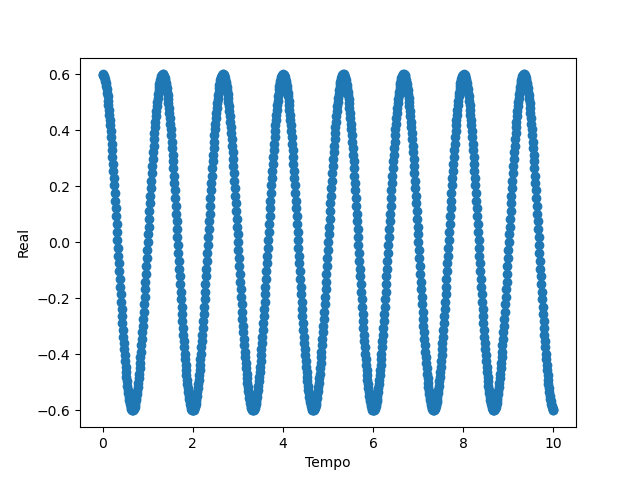
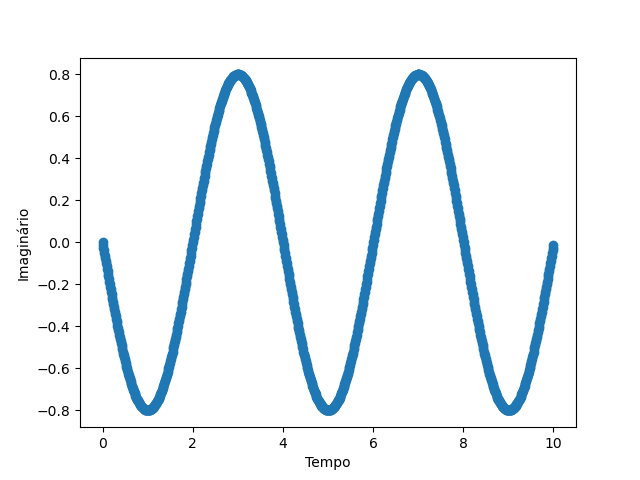
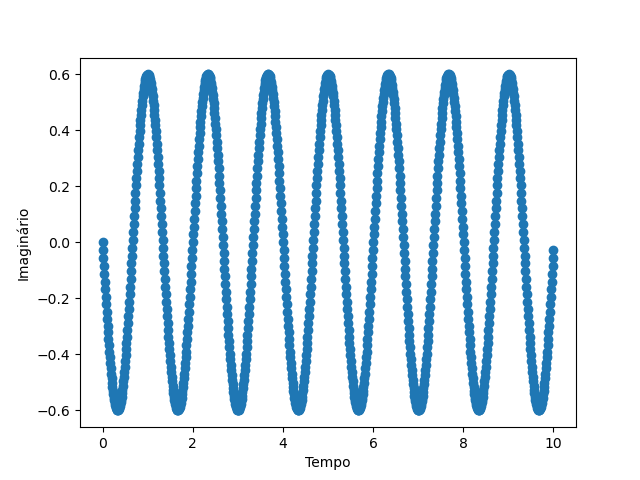
Com a biblioteca, em primeiro temos uma curva estacionária e em segundo, uma curva que há movimento temporal:

Existe uma dificuldade de controlar essa curva visto que o V(x,t) oferece pouquissímos graus de liberdade para o controle ótimo, além disso há uma representação da curva em função do tempo e espaço o que é inviável pois o espaço de solução é $R^{2}$.

Para contornar esse problema recorremos a representação por meio da notação de Dirac, que retira a contribuição espacial e relaciona energia de estado. O problema que incialmente era uma matriz $R^{2}$ se torna 2x2, afinal, são dois estados de energia.

$$\frac{\partial}{\partial t}\Psi = -\frac{iH}{\hbar}\Psi$$

Ademais, é necessário transportar essa equação para a notação de bras e kets utilizada em controle, computação e mecânica quântica moderna.

Ket e Bras - Controle Quântico

$$\frac{\partial}{\partial t}\ket{\Psi} = -\frac{iH}{\hbar}\ket{\Psi}$$

Para a equação acima, a solução analítica se da por $\ket{\Psi(t)} = e^{\frac{-iHt}{\hbar}}\ket{\Psi_0}$, onde H é um hamiltoniano. Então teremos uma exponencial matricial, que deve ser resolvida por polinômio de Taylor. O Hamiltoniano abaixo foi desenvolvido a partir do livro do Professor Piza (2003).

$$ H_0 = \left(\begin{array}{cc} 0 & 0\\ 0 & (\frac{-3i\pi t}{2} - \frac{-i\pi t}{2}) \end{array}\right) $$

Outro hamiltoniano possível é aquele em que as energias ficam na diagonal principal, dessa forma, obtemos:

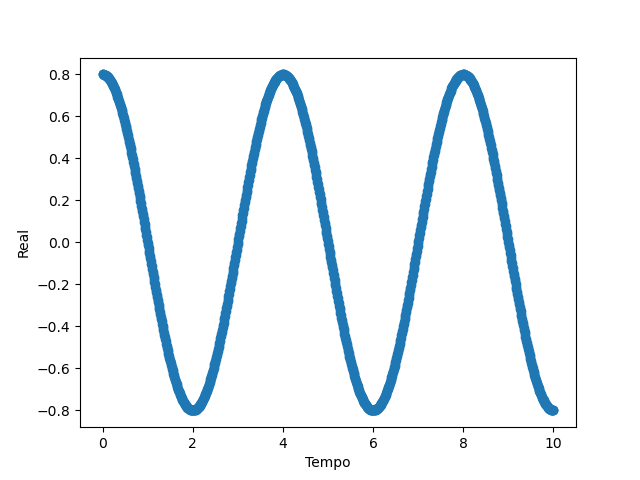
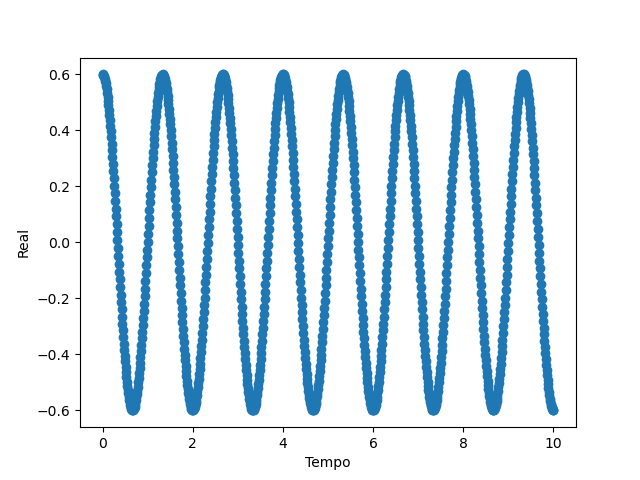
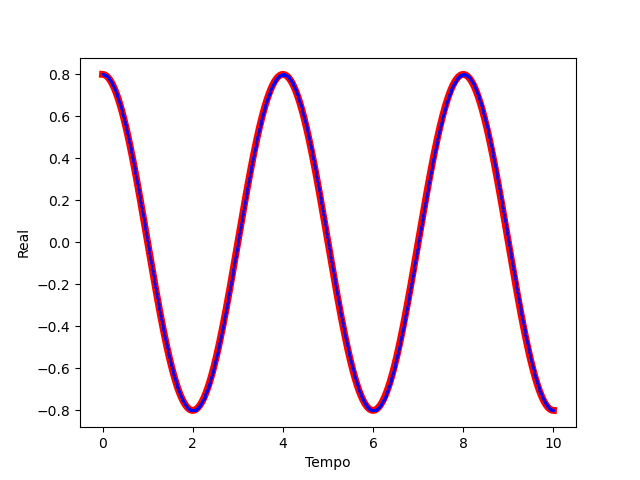
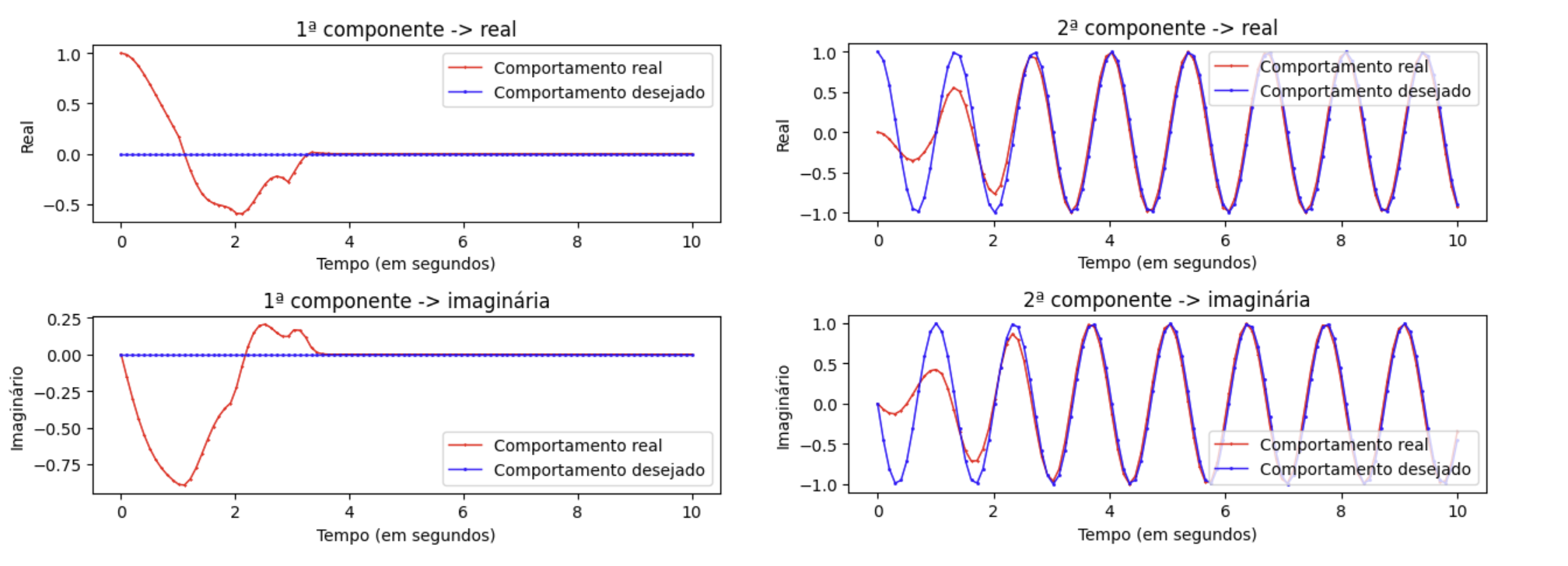
$$ H_0 = \left(\begin{array}{cc} \frac{-i\pi t}{2} & 0\\ 0 & \frac{-3i\pi t}{2} \end{array}\right) $$

Portanto, os gráficos abaixo revelam o resultado da equação $\ket{\Psi(t)} = H_0\ket{\Psi_0} = \ket{\Psi(t)} = H_0(0.80\cdot\ket 0 + 0.60\cdot\ket 1)$, real e imaginário.

Gráfico - Real

Gráfico - Imaginário

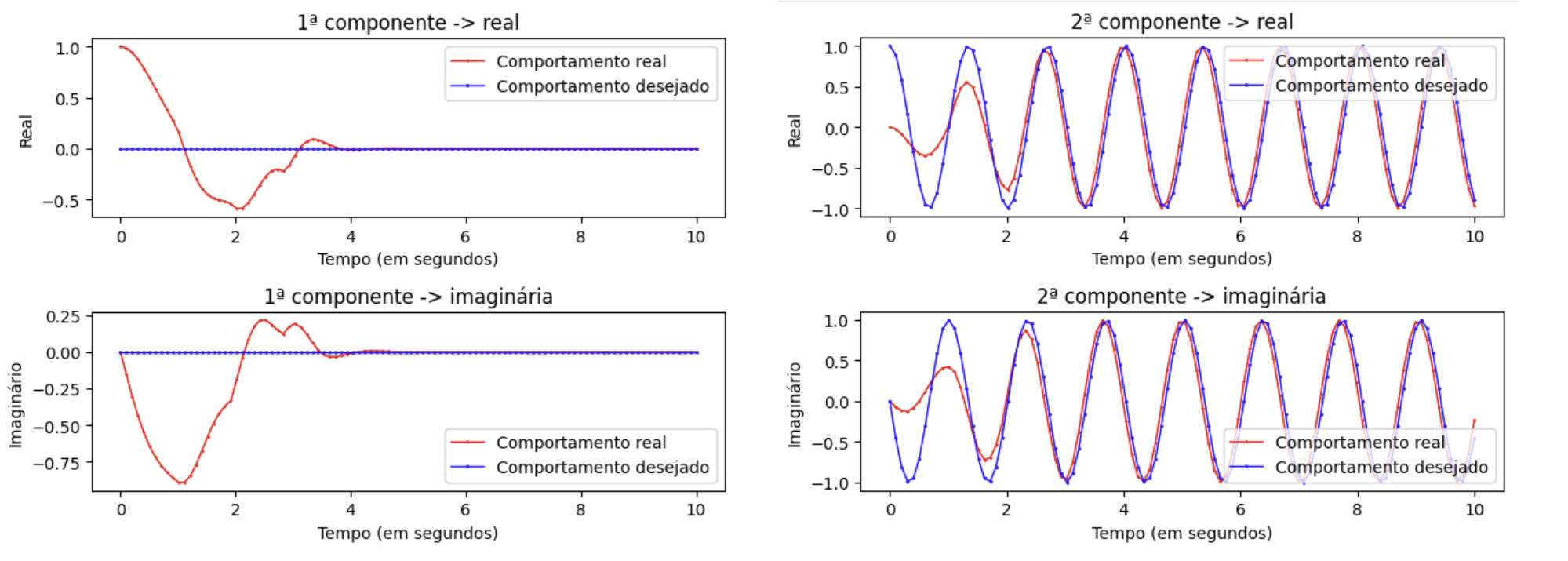
O objetivo do controle é fazer com que qualquer outro estado consiga oscilar de acordo com o estado desejado. No entanto, o processo analítico não é replicável em laboratório, dessa forma, devemos usar aproximações para a derivada. O arquivo Heisenberg-Euler-Runge_Kutta, na pasta testes-iniciais, estabelece uma comparação entre o ideal e a aproximação realizada pelo algoritmo de Runge-Kutta.

Gráfico - Real: Aproximação

Gráfico - Imaginário: Aproximação

Comparação

Atividade 4 - Preparação dos estados quânticos

Por meio da equação de erro, estabelecida na atividade anterior, $E = \sum_{n = p}^{p+N_h}||\Psi_d(x,t) - \Psi_{i}^n(u, x,t)||^{2}$, e limitando o valor do controle entre $-0{,}75 \leq u(t) \leq 0{,}75$ e utilizando os Hamiltonianos já testados, faz-se a preparação de estados. O objetivo é partir do estado $1\ket{0}+0\ket{1}$ e alcançar o estado $0\ket{0}+1\ket{1}$.

Nessa etapa foram utilizados três algoritmos de otimização, o L-BFGS-B, o Método de Newton Truncado e a Evolução diferencial. Note que a equação de erro é ótima para algoritmos baseados em gradiente como os dois primeiros citados, no entanto, ambos apresentam diferenças de resultados, diferenças na escala de $10^{-3}$. Desse modo, as imagens a seguir estão relacionadas com o uso do algoritmo L-BFGS-B.

Horizonte 3

Horizonte 10

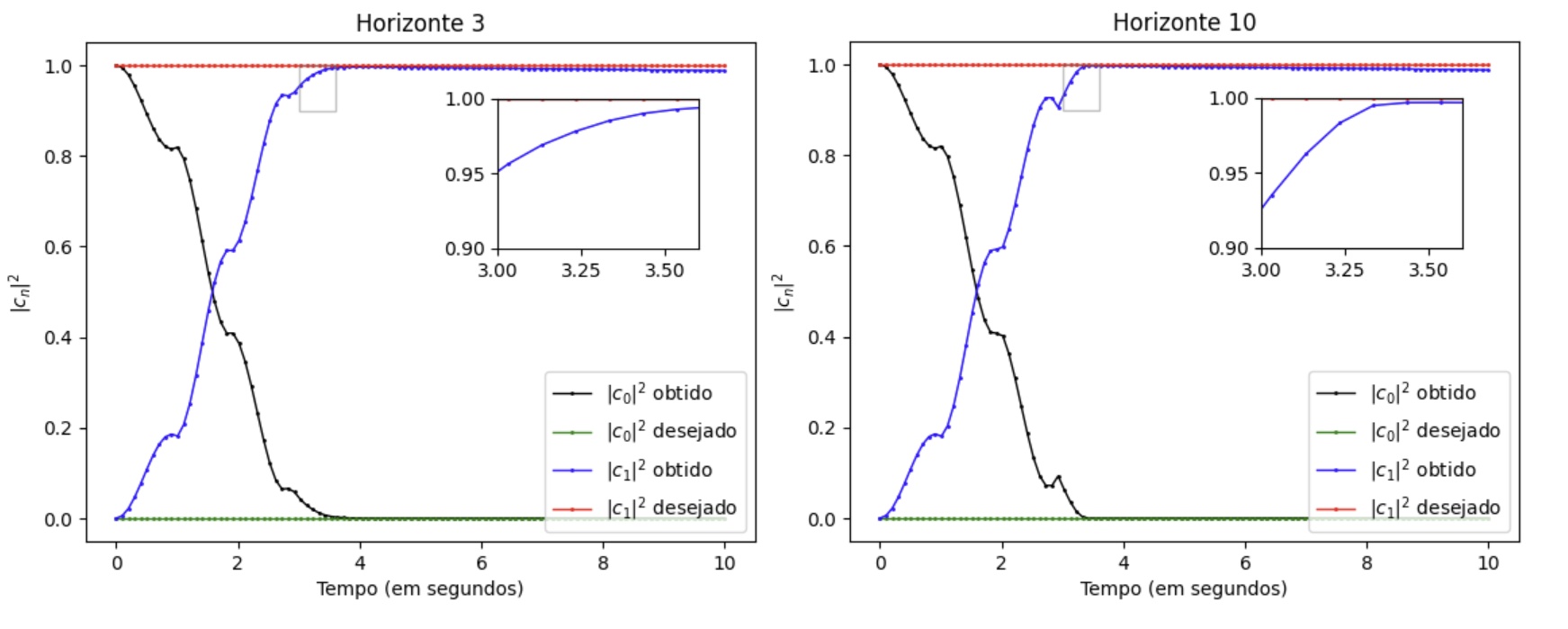
O ponto interessante do uso do MPC é a possibilidade de ajuste de horizonte e quanto maior, melhor será a aproximação da curvatura, no entanto, maior complexidade/força é demandada. Além dessas comparações, pode-se analisar as constantes do sistema quântico. Perceba que, por meio do gráfico abaixo, o horizonte 3 não alcança totalmente o valor 1.00, além disso, ele demora alguns segundos a mais, quando comparado a projeção de horizonte maior, para alcançar um valor objetivo.

Comparação entre os horizontes

Atividade 5 - MPC para sistemas quânticos abertos

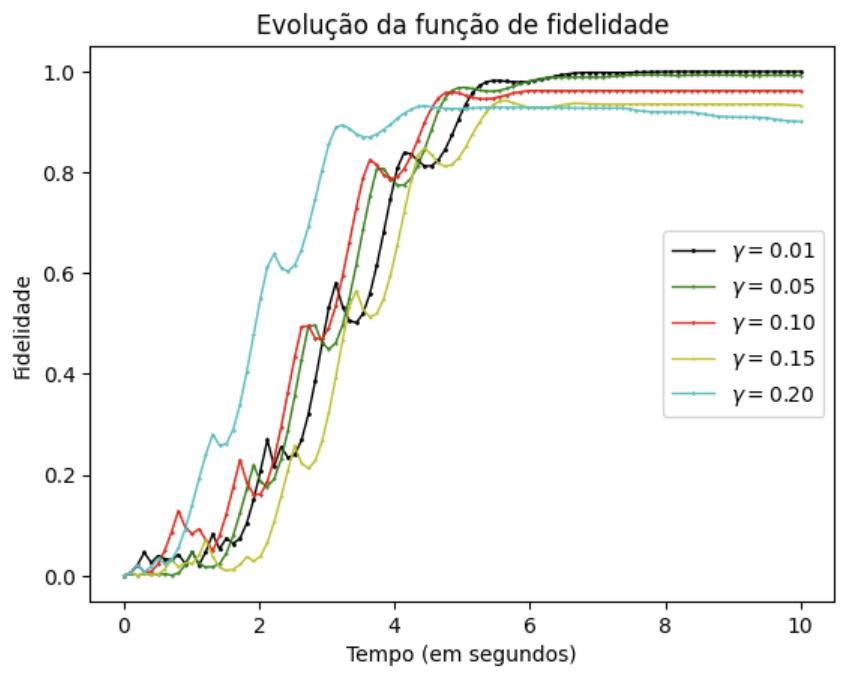
Dada a efetividade do controlador para sistemas fechados, torna-se necessário verificar a sua atuação em sistemas abertos. Para realizar tal análise, recorre-se a equação de Lindblad, a qual, pode ser descrita como:

$$ \frac{\partial \rho_t}{\partial t} = -i [H, \rho_t] + L(\rho_t) $$

A equação de Lindblad e a equação de Schrödinger são correlatas, de modo que, ambas podem representar uma determinada situação de um sistema, seja pelo estado, $\psi(t)$ ou pela matriz de densidade $\rho_t$. A matriz de densidade pode ser definida como produto interno dos estados, $\rho_t = \ket{\psi(t)}\bra{\psi(t)}$, de forma que, a preparação de estados proposta anteriormente, iniciar em $1\ket{0}+0\ket{1}$ e alcançar o estado $0\ket{0}+1\ket{1}$, torne-se, iniciar em

$$ \rho_0 = \left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right) $$

e alcançar

$$ \rho_f = \left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) $$

A primeira parcela representa o sistema quântico que se deseja manipular, enquanto a segunda parcela, $L(\rho_t) = \sum_i \gamma [L_i\rho_t L_i^\dagger - \frac{1}{2}{L_i^\dagger L_i, \rho}]$, refere-se a atuação com o ambiente externo. Para um sistema simples, $L_i = \sigma_z/\sqrt{2}$, a matriz de pauli multiplicada por um fator. Sabendo que o experimento com sistemas fechados alcança uma fidelidade de $99{,}99%$, abaixo, demonstra-se como o ambiente externo afeta tal fidelidade.

GabrielSiqueira1/MPC-Controle-Quantico