DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model Sampling in Around 10 Steps

The official code for the paper DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model Sampling in Around 10 Steps (Neurips 2022 Oral) and DPM-Solver++: Fast Solver for Guided Sampling of Diffusion Probabilistic Models by Cheng Lu, Yuhao Zhou, Fan Bao, Jianfei Chen, Chongxuan Li and Jun Zhu.

DPM-Solver (and the improved version DPM-Solver++) is a fast dedicated high-order solver for diffusion ODEs with the convergence order guarantee. DPM-Solver is suitable for both discrete-time and continuous-time diffusion models without any further training. Experimental results show that DPM-Solver can generate high-quality samples in only 10 to 20 function evaluations on various datasets.

ADM with DPM-Solver:

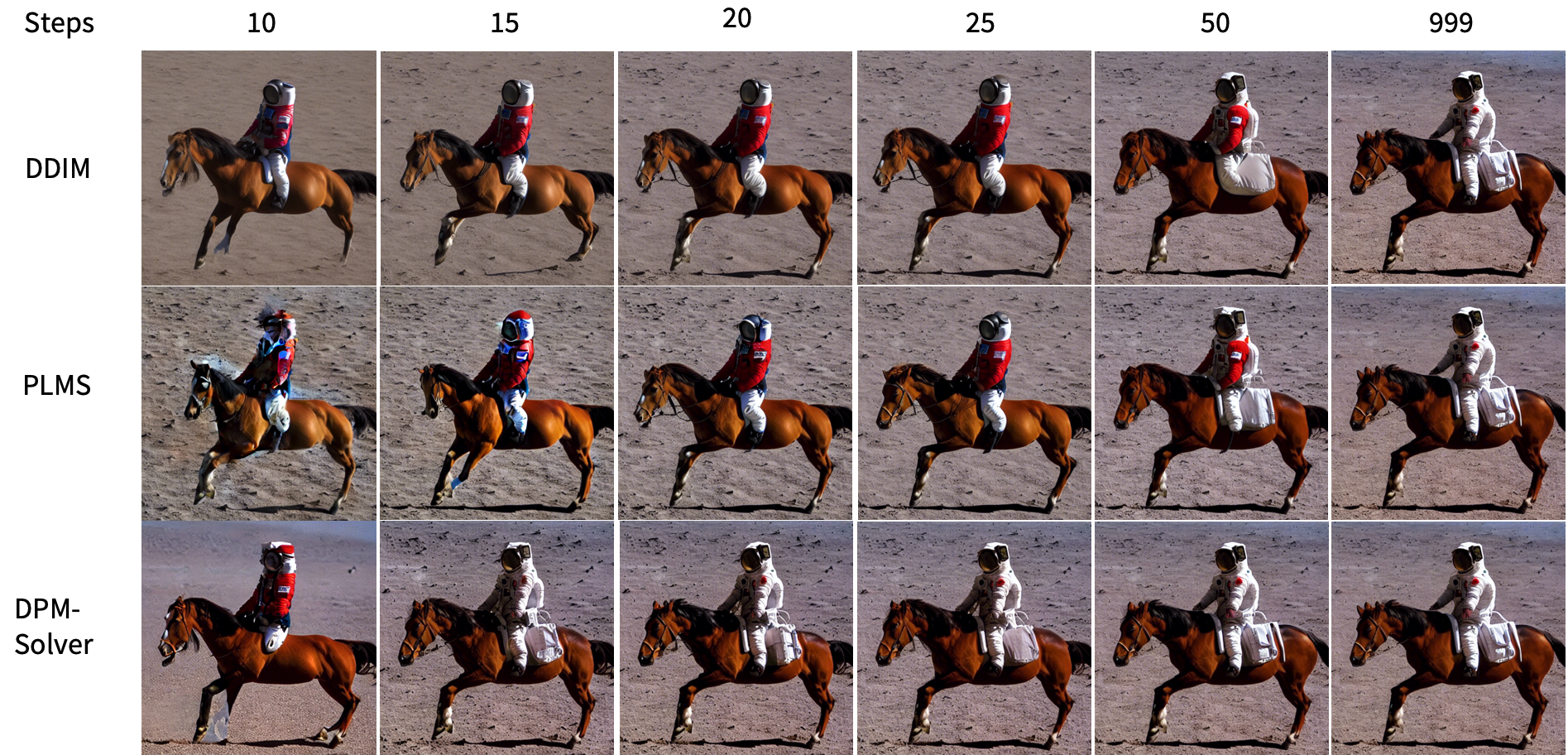
Stable-Diffusion with DPM-Solver++:

Jiafeng:

Reproduce the backward experiments:

Set up the envoronment of expample_v2 according to its readm me.
try the following cmd:

# with backward euler on
python scripts/txt2img.py --prompt "a photograph of an astronaut reading a book" --dpm_solver --ddim_steps 10 --backward-euler

# with backward euler off
python scripts/txt2img.py --prompt "a photograph of an astronaut reading a book" --dpm_solver --ddim_steps 10

News

2022-10-26. We have updated the DPM-Solver v2.0, a more stable version for high-resolutional image synthesis tasks. We have the following upgrades:
- We support the discrete-time DPMs by implementing a picewise linear interpolation of $\log\alpha_t$ for the NoiseScheduleVP.
  
  We strongly recommend to use the new implementation for discrete-time DPMs, especially for high-resolutional image synthesis. You can set schedule='discrete' to use the corresponding noise schedule. We also change the mapping between discrete-time inputs and continuous-time inputs in the model_wrapper, which has a consistent converged results with the other solvers.
- We change the API for model_wrapper:
  - We support four types of diffusion models: noise prediction model, data prediction model, velocity prediction model, score function.
  - We support unconditional sampling, classifier guidance sampling and classifier-free guidance sampling.
- We support new algorithms for DPM-Solver, which greatly improve the high-resolutional image sample quality by guided sampling.
  - We support both the noise prediction model $\epsilon_\theta(x_t,t)$ and the data prediction model $x_\theta(x_t,t)$. For the data prediction model, we further support the dynamic thresholding introduced by Imagen.
  - We support both singlestep solver (i.e. Runge-Kutta-like solver) and multistep solver (i.e. Adams-Bashforth-like solver) for DPM-Solver, including order 1, 2, 3.

Supported Models and Algorithms

Models

We support the following four types of diffusion models. You can set the model type by the argument model_type in the function model_wrapper.

Model Type	Training Objective	Example Paper
"noise": noise prediction model $\epsilon_\theta$	$E_{x_{0},\epsilon,t}\left[\omega_1(t)\|\|\epsilon_\theta(x_t,t)-\epsilon\|\|_2^2\right]$	DDPM, Stable-Diffusion
"x_start": data prediction model $x_\theta$	$E_{x_0,\epsilon,t}\left[\omega_2(t)\|\|x_\theta(x_t,t)-x_0\|\|_2^2\right]$	DALL·E 2
"v": velocity prediction model $v_\theta$	$E_{x_0,\epsilon,t}\left[\omega_3(t)\|\|v_\theta(x_t,t)-(\alpha_t\epsilon - \sigma_t x_0)\|\|_2^2\right]$	Imagen Video
"score": marginal score function $s_\theta$	$E_{x_0,\epsilon,t}\left[\omega_4(t)\|\|\sigma_t s_\theta(x_t,t)+\epsilon\|\|_2^2\right]$	ScoreSDE

Sampling Types

We support the following three types of sampling by diffusion models. You can set the argument guidance_type in the function model_wrapper.

Sampling Type	Equation for Noise Prediction Model	Example Paper
"uncond": unconditional sampling	$\tilde\epsilon_\theta(x_t,t)=\epsilon_\theta(x_t,t)$	DDPM
"classifier": classifier guidance	$\tilde\epsilon_\theta(x_t,t,c)=\epsilon_\theta(x_t,t)-s\cdot\sigma_t\nabla_{x_t}\log q_\phi(x_t,t,c)$	ADM, GLIDE
"classifier-free": classifier-free guidance	$\tilde\epsilon_\theta(x_t,t,c)=s\cdot \epsilon_\theta(x_t,t,c)+(1-s)\cdot\epsilon_\theta(x_t,t)$	DALL·E 2, Imagen, Stable-Diffusion

Algorithms in DPM-Solver

We support the following four algorithms. The algorithms with noise-prediction are referred to DPM-Solver w.r.t. the noise prediction model, and the algorithms with data-prediction are referred to DPM-Solver w.r.t. the data prediction model. We also support the dynamic thresholding introduced by Imagen for algorithms with data-prediction. The dynamic thresholding method can further improve the sample quality by pixel-space DPMs with large guidance scales.

Note that the model_fn for initializing DPM-Solver is always the noise prediction model, and for algorithms with data-prediction we further convert the noise prediction model to the data prediction model inside the implementation of DPM-Solver.

The performance of singlestep solvers (i.e. Runge-Kutta-like solvers) and the multistep solvers (i.e. Adams-Bashforth-like solvers) are different. We recommend to use different solvers for different tasks.

Method	Supported Orders	Supporting Thresholding	Remark
noise-prediction, singlestep	1, 2, 3	No	Recommended for unconditional sampling (with order = 3). See this paper.
noise-prediction, multistep	1, 2, 3	No
data-prediction, singlestep	1, 2, 3	Yes
data-prediction, multistep	1, 2, 3	Yes	Recommended for guided sampling (with order = 2). See this paper.

Examples

Stable-Diffusion with DPM-Solver

We provide an example of stable diffusion with DPM-Solver in example_v2/stable-diffusion. DPM-Solver can greatly accelerate the sampling speed of the original stable-diffusion.

ScoreSDE with DPM-Solver

We provide a pytorch example and a JAX example in example_v2/ which apply DPM-Solver for Yang Song's score_sde repo on CIFAR-10.

Other Examples

Coming soon...

Use DPM-Solver in your own code

It is very easy to combine DPM-Solver with your own diffusion models. We support both Pytorch and JAX code. You can just copy the file dpm_solver_pytorch.py or dpm_solver_jax.py to your own code files and import it.

In each step, DPM-Solver needs to compute the corresponding $\alpha_t$, $\sigma_t$ and $\lambda_t$ of the noise schedule. We support the commonly-used variance preserving (VP) noise schedule for both discrete-time and continuous-time DPMs:

For discrete-time DPMs, we support a picewise linear interpolation of $\log\alpha_t$ in the NoiseScheduleVP class. It can support all types of VP noise schedules.
For continuous-time DPMs, we support both linear schedule (as used in DDPM and ScoreSDE) and cosine schedule (as used in improved-DDPM) in the NoiseScheduleVP class.

Moreover, DPM-Solver is designed for the continuous-time diffusion ODEs. For discrete-time diffusion models, we also implement a wrapper function to convert the discrete-time diffusion models to the continuous-time diffusion models in the model_wrapper function.

Suggestions for the Detailed Settings

We recommend to use the following two types of solvers for different tasks:

3rd-order (noise-prediction + singlestep) DPM-Solver:

## Define the model and noise schedule (see examples below) 
## ....

## Define DPM-Solver and compute the sample.
dpm_solver = DPM_Solver(model_fn, noise_schedule)

## Steps in [10, 20] can generate quite good samples.
## And steps = 20 can almost converge.
x_sample = dpm_solver.sample(
    x_T,
    steps=20,
    order=3,
    skip_type="time_uniform",
    method="singlestep",
)

2nd-order (data-prediction + multistep) DPM-Solver:

For general DPMs (e.g. latent-space DPMs):

## Define the model and noise schedule (see examples below) 
## ....

## Define DPM-Solver and compute the sample.
dpm_solver = DPM_Solver(model_fn, noise_schedule, predict_x0=True)

## Steps in [10, 20] can generate quite good samples.
## And steps = 20 can almost converge.
x_sample = dpm_solver.sample(
    x_T,
    steps=20,
    order=2,
    skip_type="time_uniform",
    method="multistep",
)

For DPMs trained on bounded data (e.g. pixel-space images), we further support the dynamic thresholding method introduced by Imagen by setting thresholding = True. The dynamic thresholding method can greatly improve the sample quality of pixel-space DPMs by guided sampling with large guidance scales.

## Define the model and noise schedule (see examples below) 
## ....

## Define DPM-Solver and compute the sample.
dpm_solver = DPM_Solver(model_fn, noise_schedule, predict_x0=True,
                        thresholding=True, max_val=1.0)

## Steps in [10, 20] can generate quite good samples.
## And steps = 20 can almost converge.
x_sample = dpm_solver.sample(
    x_T,
    steps=20,
    order=2,
    skip_type="time_uniform",
    method="multistep",
)

Specifically, we have the following suggestions:

For unconditional sampling:
- For obtaining a not too bad sample as fast as possible, use the 2nd-order (data-prediction + multistep) DPM-Solver with steps <= 10.
- For obtaining a good but not converged sample, use the 3rd-order (noise-prediction + singlestep) DPM-Solver with steps = 15.
- (Recommended) For obtaining an almost converged sample, use the 3rd-order (noise-prediction + singlestep) DPM-Solver with steps = 20.
- For obtaining an absolutely converged sample, use the 3rd-order (noise-prediction + singlestep) DPM-Solver with steps = 50.
For guided sampling (especially with large guidance scales):
- Use the 2nd-order (data-prediction + multistep) DPM-Solver for all steps.
- For pixel-space DPMs (i.e. DPMs trained on images), set thresholding = True; else (e.g. latent-space DPMs) set thresholding = False.
- Choices for steps:
  - For obtaining a not too bad sample as fast as possible, use steps <= 10.
  - For obtaining a good but not converged sample, use steps = 15.
  - (Recommended) For obtaining an almost converged sample, use steps = 20.
  - For obtaining an absolutely converged sample, use steps = 50.

Example: Unconditional Sampling by DPM-Solver

We recommend to use the 3rd-order (noise-prediction + singlestep) DPM-Solver. Here is an example for discrete-time DPMs:

from dpm_solver_pytorch import NoiseScheduleVP, model_wrapper, DPM_Solver

## You need to firstly define your model and the extra inputs of your model,
## And initialize an `x_T` from the standard normal distribution.
## `model` has the format: model(x_t, t_input, **model_kwargs).
## If your model has no extra inputs, just let model_kwargs = {}.

## If you use discrete-time DPMs, you need to further define the
## beta arrays for the noise schedule.

# model = ....
# model_kwargs = {...}
# x_T = ...
# betas = ....

## 1. Define the noise schedule.
noise_schedule = NoiseScheduleVP(schedule='discrete', betas=betas)

## 2. Convert your discrete-time `model` to the continuous-time
## noise prediction model. Here is an example for a diffusion model
## `model` with the noise prediction type ("noise") .
model_fn = model_wrapper(
    model,
    noise_schedule,
    model_type="noise",  # or "x_start" or "v" or "score"
    model_kwargs=model_kwargs,
)

## 3. Define dpm-solver and sample by singlestep DPM-Solver.
## (We recommend singlestep DPM-Solver for unconditional sampling)
## You can adjust the `steps` to balance the computation
## costs and the sample quality.
dpm_solver = DPM_Solver(model_fn, noise_schedule)

## You can use steps = 10, 12, 15, 20, 25, 50, 100.
## Empirically, we find that steps in [10, 20] can generate quite good samples.
## And steps = 20 can almost converge.
x_sample = dpm_solver.sample(
    x_T,
    steps=20,
    order=3,
    skip_type="time_uniform",
    method="singlestep",
)

Example: Classifier Guidance Sampling by DPM-Solver

We recommend to use the 2nd-order (data-prediction + multistep) DPM-Solver, especially for large guidance scales. Here is an example for discrete-time DPMs:

from dpm_solver_pytorch import NoiseScheduleVP, model_wrapper, DPM_Solver

## You need to firstly define your model and the extra inputs of your model,
## And initialize an `x_T` from the standard normal distribution.
## `model` has the format: model(x_t, t_input, **model_kwargs).
## If your model has no extra inputs, just let model_kwargs = {}.

## If you use discrete-time DPMs, you need to further define the
## beta arrays for the noise schedule.

## For classifier guidance, you need to further define a classifier function,
## a guidance scale and a condition variable.

# model = ....
# model_kwargs = {...}
# x_T = ...
# condition = ...
# betas = ....
# classifier = ...
# classifier_kwargs = {...}
# guidance_scale = ...

## 1. Define the noise schedule.
noise_schedule = NoiseScheduleVP(schedule='discrete', betas=betas)

## 2. Convert your discrete-time `model` to the continuous-time
## noise prediction model. Here is an example for a diffusion model
## `model` with the noise prediction type ("noise") .
model_fn = model_wrapper(
    model,
    noise_schedule,
    model_type="noise",  # or "x_start" or "v" or "score"
    model_kwargs=model_kwargs,
    guidance_type="classifier",
    condition=condition,
    guidance_scale=guidance_scale,
    classifier_fn=classifier,
    classifier_kwargs=classifier_kwargs,
)

## 3. Define dpm-solver and sample by multistep DPM-Solver.
## (We recommend multistep DPM-Solver for conditional sampling)
## You can adjust the `steps` to balance the computation
## costs and the sample quality.

dpm_solver = DPM_Solver(model_fn, noise_schedule, predict_x0=True)

## If the DPM is defined on pixel-space images, you can further
## set `thresholding=True`. e.g.:

# dpm_solver = DPM_Solver(model_fn, noise_schedule, predict_x0=True,
#   thresholding=True)


## You can use steps = 10, 12, 15, 20, 25, 50, 100.
## Empirically, we find that steps in [10, 20] can generate quite good samples.
## And steps = 20 can almost converge.
x_sample = dpm_solver.sample(
    x_T,
    steps=20,
    order=2,
    skip_type="time_uniform",
    method="multistep",
)

Example: Classifier-Free Guidance Sampling by DPM-Solver

We recommend to use the 2nd-order (data-prediction + multistep) DPM-Solver, especially for large guidance scales. Here is an example for discrete-time DPMs:

from dpm_solver_pytorch import NoiseScheduleVP, model_wrapper, DPM_Solver

## You need to firstly define your model and the extra inputs of your model,
## And initialize an `x_T` from the standard normal distribution.
## `model` has the format: model(x_t, t_input, cond, **model_kwargs).
## If your model has no extra inputs, just let model_kwargs = {}.

## If you use discrete-time DPMs, you need to further define the
## beta arrays for the noise schedule.

## For classifier-free guidance, you need to further define a guidance scale,
## a condition variable and an unconditioanal condition variable.

# model = ....
# model_kwargs = {...}
# x_T = ...
# condition = ...
# unconditional_condition = ...
# betas = ....
# guidance_scale = ...

## 1. Define the noise schedule.
noise_schedule = NoiseScheduleVP(schedule='discrete', betas=betas)

## 2. Convert your discrete-time `model` to the continuous-time
## noise prediction model. Here is an example for a diffusion model
## `model` with the noise prediction type ("noise") .
model_fn = model_wrapper(
    model,
    noise_schedule,
    model_type="noise",  # or "x_start" or "v" or "score"
    model_kwargs=model_kwargs,
    guidance_type="classifier-free",
    condition=condition,
    unconditional_condition=unconditional_condition,
    guidance_scale=guidance_scale,
)

## 3. Define dpm-solver and sample by multistep DPM-Solver.
## (We recommend multistep DPM-Solver for conditional sampling)
## You can adjust the `steps` to balance the computation
## costs and the sample quality.

dpm_solver = DPM_Solver(model_fn, noise_schedule, predict_x0=True)

## If the DPM is defined on pixel-space images, you can further
## set `thresholding=True`. e.g.:

# dpm_solver = DPM_Solver(model_fn, noise_schedule, predict_x0=True,
#   thresholding=True)


## You can use steps = 10, 12, 15, 20, 25, 50, 100.
## Empirically, we find that steps in [10, 20] can generate quite good samples.
## And steps = 20 can almost converge.
x_sample = dpm_solver.sample(
    x_T,
    steps=20,
    order=2,
    skip_type="time_uniform",
    method="multistep",
)

Documentation

1. Define the noise schedule.

We support the commonly-used variance preserving (VP) noise schedule for both discrete-time and continuous-time DPMs:

1.1. Discrete-time DPMs

We support a picewise linear interpolation of $\log\alpha_{t}$ in the NoiseScheduleVP class. It can support all types of VP noise schedules.

We need either the $\beta_i$ array or the $\bar{\alpha}_i$ array (see DDPM for details) to define the noise schedule. Note that the $\bar{\alpha}_i$ in DDPM is different from the $\alpha_t$ in DPM-Solver, and the detailed relationship is:

$$ \bar{\alpha}_i = \prod (1 - \beta_k) $$

$$ \alpha_{t_i} = \sqrt{\bar{\alpha}_i} $$

Define the discrete-time noise schedule by the $\beta_i$ array:

noise_schedule = NoiseScheduleVP(schedule='discrete', betas=betas)

Or define the discrete-time noise schedule by the $\bar{\alpha}_i$ array:

noise_schedule = NoiseScheduleVP(schedule='discrete', alphas_cumprod=alphas_cumprod)

1.2. Continuous-time DPMs

We support both linear schedule (as used in DDPM and ScoreSDE) and cosine schedule (as used in improved-DDPM) for the continuous-time DPMs.

Define the continuous-time linear noise schedule:

noise_schedule = NoiseScheduleVP(schedule='linear', continuous_beta_0=0.1, continuous_beta_1=20.)

Define the continuous-time cosine noise schedule:

noise_schedule = NoiseScheduleVP(schedule='cosine')

2. Wrap your model to a continuous-time noise predicition model.

For a given diffusion model with an input of the time label (may be discrete-time labels (i.e. 0 to 999) or continuous-time times (i.e. 0 to 1)), and the output type of the model may be "noise" or "x_start" or "v" or "score", we wrap the model function to the following format:

model_fn(x, t_continuous) -> noise

where t_continuous is the continuous time labels (i.e. 0 to 1), and the output type of the model is "noise", i.e. a noise prediction model. And we use the continuous-time noise prediction model model_fn for DPM-Solver.

Note that DPM-Solver only needs the noise prediction model (the $\epsilon_\theta(x_t, t)$ model, also as known as the "mean" model), so for diffusion models which predict both "mean" and "variance" (such as improved-DDPM), you need to firstly define another function by yourself to only output the "mean".

2.1. Sampling without Guidance

After defining the noise schedule, we need to further wrap the model to a continuous-time noise prediction model. The given model has the following format:

model(x_t, t_input, **model_kwargs) -> noise | x_start | v | score

And we wrap the model by:

model_fn = model_wrapper(
    model,
    noise_schedule,
    model_type=model_type, # "noise" or "x_start" or "v" or "score"
    model_kwargs=model_kwargs,
)

where model_kwargs is the additional inputs of the model, and the model_type can be "noise" or "x_start" or "v" or "score".

2.2. Sampling with Classifier Guidance

After defining the noise schedule, we need to further wrap the model to a continuous-time noise prediction model. The given model has the following format:

model(x_t, t_input, **model_kwargs) -> noise | x_start | v | score

For DPMs with classifier guidance, we also combine the model output with the classifier gradient. We need to specify the classifier function and the guidance scale. The classifier function has the following format:

classifier_fn(x, t_input, cond, **classifier_kwargs) -> logits(x, t_input, cond)

where t_input is the same time label as in the original diffusion model model, and cond is the condition variable, and classifier_kwargs is the other inputs of the classifier function.

And we wrap the model by:

model_fn = model_wrapper(
    model,
    noise_schedule,
    model_type=model_type,  # "noise" or "x_start" or "v" or "score"
    model_kwargs=model_kwargs,
    guidance_type="classifier",
    condition=condition,
    guidance_scale=guidance_scale,
    classifier_fn=classifier,
    classifier_kwargs=classifier_kwargs,
)

where model_kwargs is the additional inputs of the model, and the model_type can be "noise" or "x_start" or "v" or "score", and guidance_scale is the classifier guidance scale, and condition is the conditional input of the classifier.

2.3. Sampling with Classifier-free Guidance

After defining the noise schedule, we need to further wrap the model to a continuous-time noise prediction model. The given model has the following format:

model(x_t, t_input, cond, **model_kwargs) -> noise | x_start | v | score

Note that for classifier-free guidance, the model needs another input cond. And if cond is a special variable unconditional_condition, the model output is the unconditional DPM output.

And we wrap the model by:

model_fn = model_wrapper(
    model,
    noise_schedule,
    model_type=model_type,  # "noise" or "x_start" or "v" or "score"
    model_kwargs=model_kwargs,
    guidance_type="classifier-free",
    condition=condition,
    unconditional_condition=unconditional_condition,
    guidance_scale=guidance_scale,
)

2.4. Implementation Details for the Time Inputs

Below we introduce the detailed mapping between the discrete-time labels and the continuous-time times. However, to use DPM-Solver, it is not necessary to understand the following details.

Discrete-time DPM-Solver

For discrete-time DPMs, the noise prediction model noise-prediction is trained for the discrete-time labels from $0$ to $N-1$. Therefore, we sample from the discrete-time label $N - 1$ (e.g. 999) to the discrete-time label $0$. We convert the discrete-time labels in $[0, N-1]$ to the continuous-time times $(0,1]$ by

$$ t_{\text{discrete}} = 1000 * \left(t_{\text{continuous}} - \frac{1}{N}\right), $$

i.e. we map the discrete-time label $0$ to the continuous-time time $\frac{1}{N}$, and the discrete-time label $N-1$ to the continuous-time time $1$. Therefore, sampling from the discrete time from $N-1$ to $0$ is corresponding to sampling from the continuous time from $1$ to $\frac{1}{N}$.

Continuous-time DPM-Solver

For continuous-time DPMs from defined by $t \in [0,1]$, we simply wrap the model to accept only $x_t$ and $t$. Note that for continuous-time DPMs, we do not modify the time inputs.

3. Define DPM-Solver

After defining the model_fn by the function model_wrapper, we can further use model_fn to define DPM-Solver and compute samples.

Method	Supported Orders	Support Thresholding	Remark
noise-prediction, singlestep	1, 2, 3	No	Recommended for unconditional sampling (with order = 3)
noise-prediction, multistep	1, 2, 3	No
data-prediction, singlestep	1, 2, 3	Yes
data-prediction, multistep	1, 2, 3	Yes	Recommended for guided sampling (with order = 2)

For DPM-Solver w.r.t. noise-prediction, define

dpm_solver = DPM_Solver(model_fn, noise_schedule)

For DPM-Solver w.r.t. data-prediction, define

dpm_solver = DPM_Solver(model_fn, noise_schedule, predict_x0=True)

For DPM-Solver w.r.t. data-prediction and applying dynamic thresholding, define

dpm_solver = DPM_Solver(model_fn, noise_schedule, predict_x0=True,
                        thresholding=True, max_val=1.0)

You can use dpm_solver.sample to quickly sample from DPMs. This function computes the ODE solution at time t_end by DPM-Solver, given the initial x at time t_start.

We support the following algorithms:

Singlestep DPM-Solver. We combine all the singlestep solvers with order <= order to use up all the function evaluations (steps).
Multistep DPM-Solver.
Fixed order singlestep DPM-Solver (i.e. DPM-Solver-1, DPM-Solver-2 and DPM-Solver-3).
Adaptive step size DPM-Solver. (i.e. DPM-Solver-12 and DPM-Solver-23)

We support three types of skip_type for the choice of intermediate time steps:

logSNR: uniform logSNR for the time steps. Recommended for low-resolutional images.
time_uniform: uniform time for the time steps. Recommended for high-resolutional images.
time_quadratic: quadratic time for the time steps.

3.1. Sampling by Singlestep DPM-Solver

We combine all the singlestep solvers with order <= order to use up all the function evaluations (steps). The total number of function evaluations (NFE) == steps.

For discrete-time DPMs, we do not need to specify the t_start and t_end. The default setting is to sample from the discrete-time label $N-1$ to the discrete-time label $0$. For example,

## discrete-time DPMs
x_sample = dpm_solver.sample(
    x_T,
    steps=20,
    order=3,
    skip_type="time_uniform",
    method="singlestep",
)

For continuous-time DPMs, we sample from t_start=1.0 (the default setting) to t_end. We recommend t_end=1e-3 for steps <= 15, and t_end=1e-4 for steps > 15. For example:

x_sample = dpm_solver.sample(
    x_T,
    t_end=1e-3,
    steps=12,
    order=3,
    skip_type="time_uniform",
    method="singlestep",
)

## continuous-time DPMs
x_sample = dpm_solver.sample(
    x_T,
    t_end=1e-4,
    steps=20,
    order=3,
    skip_type="time_uniform",
    method="singlestep",
)

Implementation Details of Singlestep DPM-Solver

Given a fixed NFE == steps, the sampling procedure is:

If order == 1:
- Denote K = steps. We use K steps of DPM-Solver-1 (i.e. DDIM).
If order == 2:
- Denote K = (steps // 2) + (steps % 2). We take K intermediate time steps for sampling.
- If steps % 2 == 0, we use K steps of singlestep DPM-Solver-2.
- If steps % 2 == 1, we use (K - 1) steps of singlestep DPM-Solver-2 and 1 step of DPM-Solver-1.
If order == 3:
- Denote K = (steps // 3 + 1). We take K intermediate time steps for sampling.
- If steps % 3 == 0, we use (K - 2) steps of singlestep DPM-Solver-3, and 1 step of singlestep DPM-Solver-2 and 1 step of DPM-Solver-1.
- If steps % 3 == 1, we use (K - 1) steps of singlestep DPM-Solver-3 and 1 step of DPM-Solver-1.
- If steps % 3 == 2, we use (K - 1) steps of singlestep DPM-Solver-3 and 1 step of singlestep DPM-Solver-2.

3.2. Sampling by multistep DPM-Solver

For discrete-time DPMs, we do not need to specify the t_start and t_end. The default setting is to sample from the discrete-time label $N-1$ to the discrete-time label $0$. For example,

## discrete-time DPMs
x_sample = dpm_solver.sample(
    x_T,
    steps=20,
    order=2,
    skip_type="time_uniform",
    method="multistep",
)

For continuous-time DPMs, we sample from t_start=1.0 (the default setting) to t_end. We recommend t_end=1e-3 for steps <= 15, and t_end=1e-4 for steps > 15. For example:

x_sample = dpm_solver.sample(
    x_T,
    t_end=1e-3,
    steps=10,
    order=2,
    skip_type="time_uniform",
    method="multistep",
)

## continuous-time DPMs
x_sample = dpm_solver.sample(
    x_T,
    t_end=1e-4,
    steps=20,
    order=3,
    skip_type="time_uniform",
    method="multistep",
)

Implementation Details of Multistep DPM-Solver

We initialize the first order values by lower order multistep solvers.

Given a fixed NFE == steps, the sampling procedure is:

Denote K = steps.
If order == 1:
- We use K steps of DPM-Solver-1 (i.e. DDIM).
If order == 2:
- We firstly use 1 step of DPM-Solver-1, then use (K - 1) step of multistep DPM-Solver-2.
If order == 3:
- We firstly use 1 step of DPM-Solver-1, then 1 step of multistep DPM-Solver-2, then (K - 2) step of multistep DPM-Solver-3.

3.3. Sampling by adaptive step size DPM-Solver

For continuous-time DPMs, we recommend t_end=1e-4 for better sample quality.

We ignore steps and use adaptive step size DPM-Solver with a higher order of order. You can adjust the absolute tolerance atol and the relative tolerance rtol to balance the computatation costs (NFE) and the sample quality. For image data, we recommend atol=0.0078 (the default setting).

If order == 2, we use DPM-Solver-12 which combines DPM-Solver-1 and singlestep DPM-Solver-2.
If order == 3, we use DPM-Solver-23 which combines singlestep DPM-Solver-2 and singlestep DPM-Solver-3.

For example, to sample by DPM-Solver-12:

x_sample = dpm_solver.sample(
    x_T,
    t_end=1e-4,
    order=2,
    method="adaptive",
    rtol=0.05,
)

3.4. Sampling by Singlestep DPM-Solver-k for k = 1, 2, 3

We use DPM-Solver-order for order = 1 or 2 or 3, with total [steps // order] * order NFE.

For example, to sample by DPM-Solver-3:

x_sample = dpm_solver.sample(
    x_T,
    steps=30,
    order=3,
    skip_type="time_uniform",
    method="singlestep_fixed",
)

TODO List

Add stable-diffusion examples.
Support Diffusers.
Documentation for example code.
Clean and add the JAX code example.
Add more explanations about DPM-Solver.
Add a small jupyter example.
Add VE type noise schedule.

References

If you find the code useful for your research, please consider citing

@article{lu2022dpm,
  title={DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model Sampling in Around 10 Steps},
  author={Lu, Cheng and Zhou, Yuhao and Bao, Fan and Chen, Jianfei and Li, Chongxuan and Zhu, Jun},
  journal={arXiv preprint arXiv:2206.00927},
  year={2022}
}

Hanke98/dpm-solver

DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model Sampling in Around 10 Steps

Jiafeng:

Reproduce the backward experiments:

News

Supported Models and Algorithms

Models

Sampling Types

Algorithms in DPM-Solver

Examples

Stable-Diffusion with DPM-Solver

ScoreSDE with DPM-Solver

Other Examples

Use DPM-Solver in your own code

Suggestions for the Detailed Settings

Example: Unconditional Sampling by DPM-Solver

Example: Classifier Guidance Sampling by DPM-Solver

Example: Classifier-Free Guidance Sampling by DPM-Solver

Documentation

1. Define the noise schedule.

1.1. Discrete-time DPMs

1.2. Continuous-time DPMs

2. Wrap your model to a continuous-time noise predicition model.

2.1. Sampling without Guidance

2.2. Sampling with Classifier Guidance

2.3. Sampling with Classifier-free Guidance

2.4. Implementation Details for the Time Inputs

Discrete-time DPM-Solver

Continuous-time DPM-Solver

3. Define DPM-Solver

3.1. Sampling by Singlestep DPM-Solver

Implementation Details of Singlestep DPM-Solver

3.2. Sampling by multistep DPM-Solver

Implementation Details of Multistep DPM-Solver

3.3. Sampling by adaptive step size DPM-Solver

3.4. Sampling by Singlestep DPM-Solver-k for k = 1, 2, 3

TODO List

References