PC Skeletor is a Python library for extracting a 1d skeleton from 3d point clouds using Laplacian-Based Contraction and Semantic Laplacian-Based Contraction.
Standard Laplacian-based contraction (LBC) is prone to mal-contraction in cases where there is a significant disparity in diameter between trunk and branches. In such cases fine structures experience an over-contraction and leading to a distortion of their topological characteristics. In addition, LBC shows a topologically incorrect tree skeleton for trunk structures that have holes in the point cloud.In order to address these topological artifacts, we introduce semantic Laplacian-based contraction (S-LBC). It integrates semantic information of the point cloud into the contraction algorithm.

|

|
First install Python Version 3.7 or higher. The python package can be installed via PyPi using pip.
pip install pc-skeletorgit clone https://github.com/meyerls/pc-skeletor.git
cd pc-skeletor
pip install --upgrade pip setuptools
pip install -r requirements.txt
pip install -e .The following code performs the skeletonization algorithm on a downloaded point cloud example. It also generates an animation that includes the original point cloud and the resulting skeleton, which is exported as a gif.
import open3d as o3d
import numpy as np
from pc_skeletor import Dataset
downloader = Dataset()
trunk_pcd_path, branch_pcd_path = downloader.download_semantic_tree_dataset()
pcd_trunk = o3d.io.read_point_cloud(trunk_pcd_path)
pcd_branch = o3d.io.read_point_cloud(branch_pcd_path)
pcd = pcd_trunk + pcd_branchfrom pc_skeletor import LBC
lbc = LBC(point_cloud=pcd,
down_sample=0.008)
lbc.extract_skeleton()
lbc.extract_topology()
lbc.visualize()
lbc.show_graph(lbc.skeleton_graph)
lbc.show_graph(lbc.topology_graph)
lbc.save('./output')
lbc.animate(init_rot=np.asarray([[1, 0, 0], [0, 0, 1], [0, 1, 0]]),
steps=300,
output='./output')from pc_skeletor import SLBC
s_lbc = SLBC(point_cloud={'trunk': pcd_trunk, 'branches': pcd_branch},
semantic_weighting=30,
down_sample=0.008,
debug=True)
s_lbc.extract_skeleton()
s_lbc.extract_topology()
s_lbc.visualize()
s_lbc.show_graph(s_lbc.skeleton_graph)
s_lbc.show_graph(s_lbc.topology_graph)
s_lbc.save('./output')
s_lbc.animate(init_rot=np.asarray([[1, 0, 0], [0, 0, 1], [0, 1, 0]]), steps=300, output='./output')
Skeleton
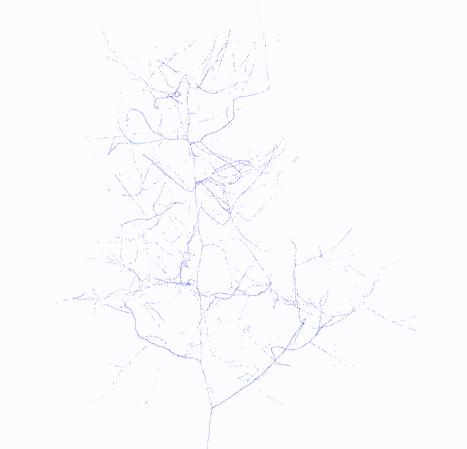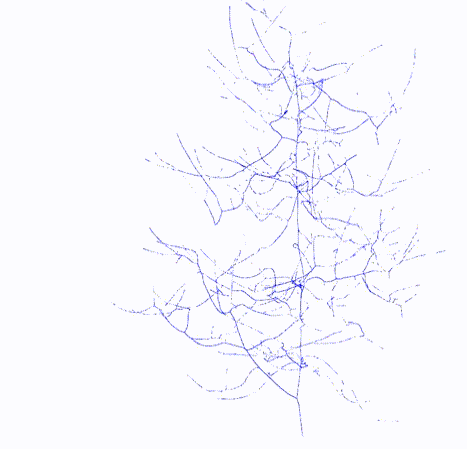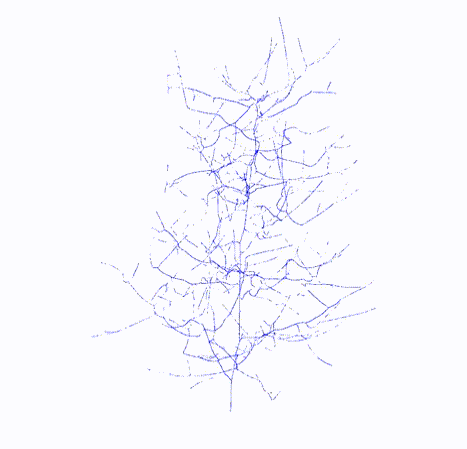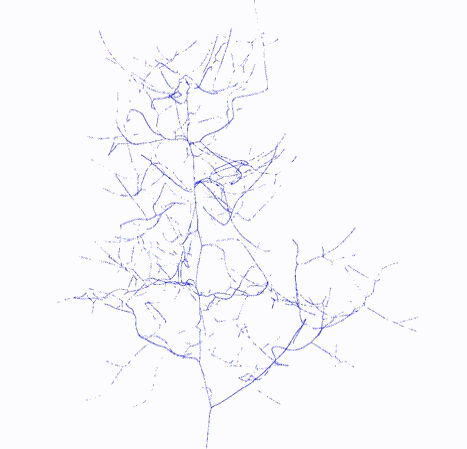
|
Topology
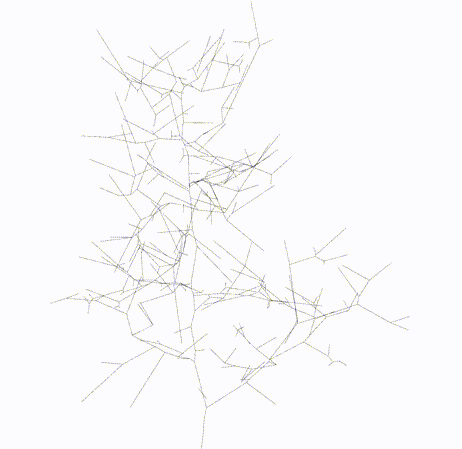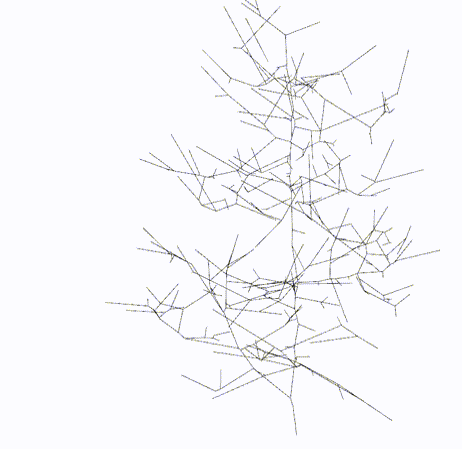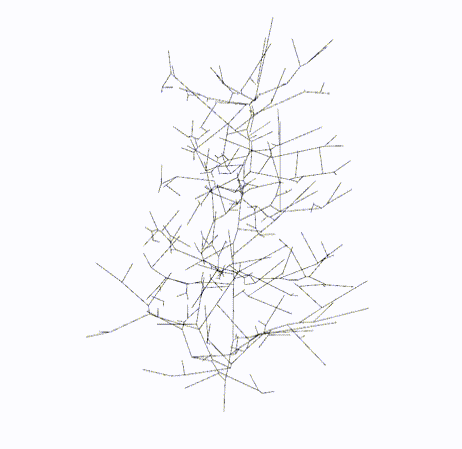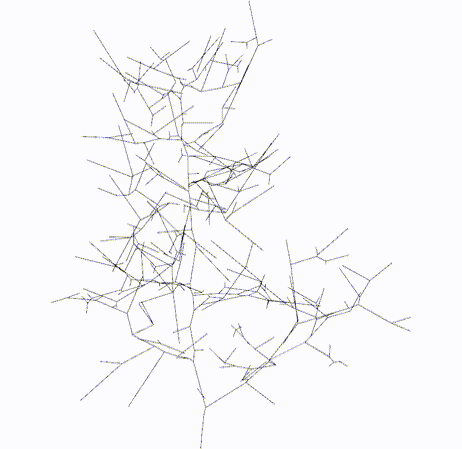
|
Skeletal Graph

|
Topology Graph
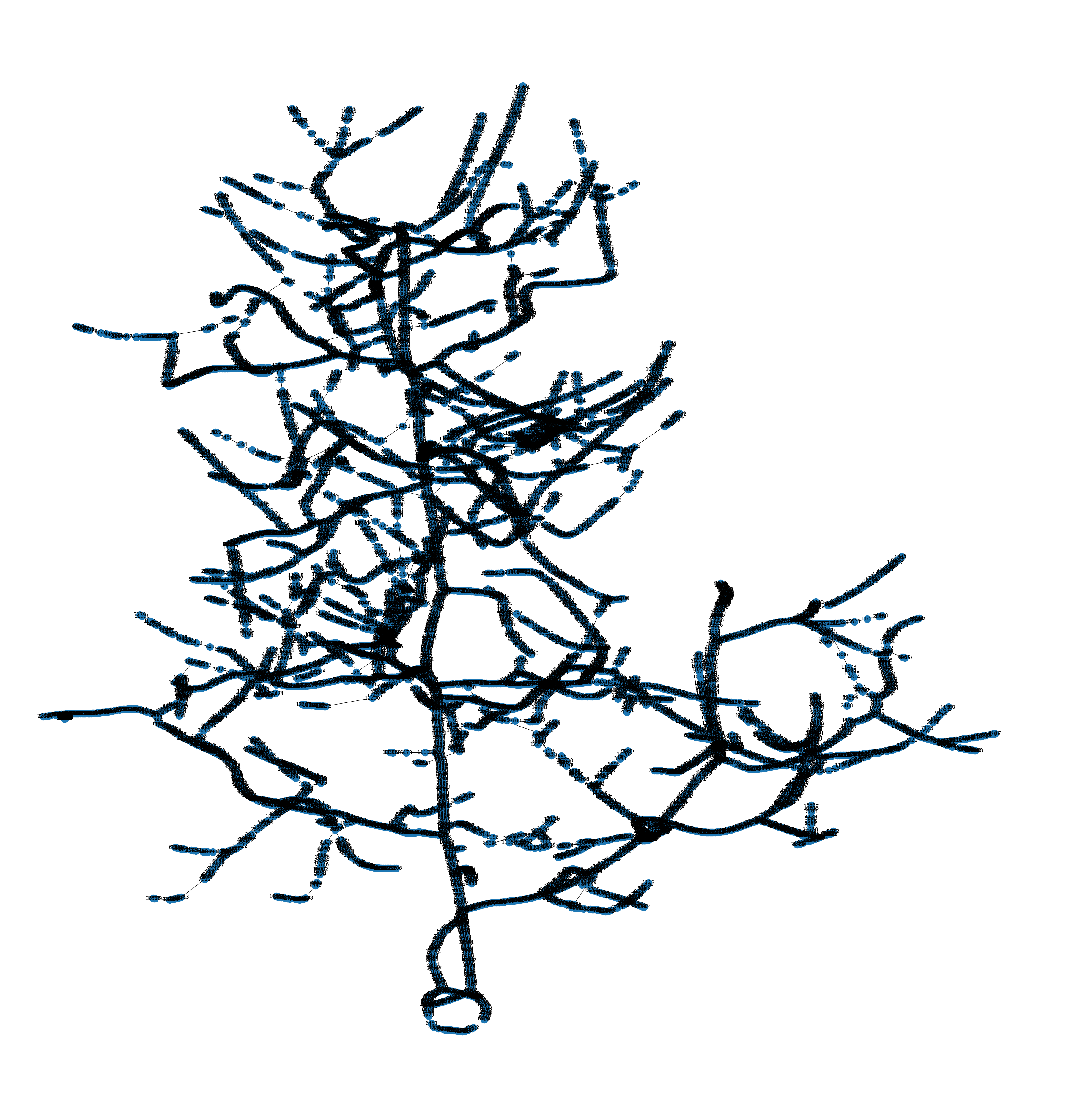
|
lbc.contracted_point_cloud: o3d.geometry.PointCloud
lbc.skeleton: o3d.geometry.PointCloud
lbc.skeleton_graph: networkx.nx
lbc.topology: o3d.geometry.LineSet
lbc.topology_graph: networkx.nxLaplacian-Based Contraction is a method based on contraction of point clouds to extract curve skeletons by iteratively contracting the point cloud. This method is robust to missing data and noise. Additionally no prior knowledge on the topology of the object has to be made.
The contraction is computed by iteratively solving the linear system
obtained from Kin-Chung Au et al.
To archive good contraction result and avoid over- and under-contraction it is necessary to initialize and update the
weights
Semantic Laplacian-Based Contraction is based on Laplacian-based contraction and simply adds semantic knowledge to the skeletonization algorithm.
Standard LBC is prone to mal-contraction in cases where there is a significant disparity in diameter between trunk and branches. In such cases fine structures experience an over- contraction and leading to a distortion of their topological characteristics. In order to address these topological artifacts, we introduce semantic Laplacian-based contraction (S-LBC). For more information please refer to the [Paper].
Our implementation of Point Cloud Skeletons via Laplacian-Based Contraction is a python reimplementation of the original Matlab code.
Computation of the discrete laplacian operator via Nonmanifold Laplace can be found in the robust-laplacians-py repository.
The Minimum Spanning Tree is computed via Mistree a open-source implementation which can be found here.
For Windows users, there might be issues installing the mistree library via python -m pip install mistree command.
If you get an error message that the Fortran compiler cannot be found, please try the following:
- Download and install this suite of compilation tools: http://www.equation.com/servlet/equation.cmd?fa=fortran
- Add the
binfolder in the installation directory to yourPATHenvironment variable - After restarting your terminal and now trying to install
mistreethis should work now. - However, upon importing the library you might face an issue with missing DLL files. You simply need to copy or move
them within the
mistreeinstallation directory, as explained here: knaidoo29/mistree#14 (comment) - Now the PC-Skeletor should be running on your Windows machine.
- Implement Point2Skeleton
- Implement L1-Medial Skeleton
- Test code
- Improve graph representation
Please cite this [Paper] if this work helps you with your research:
@misc{meyer2023cherrypicker,
title={CherryPicker: Semantic Skeletonization and Topological Reconstruction of Cherry Trees},
author={Lukas Meyer and Andreas Gilson and Oliver Scholz and Marc Stamminger},
year={2023},
eprint={2304.04708},
archivePrefix={arXiv},
primaryClass={cs.CV}
}



