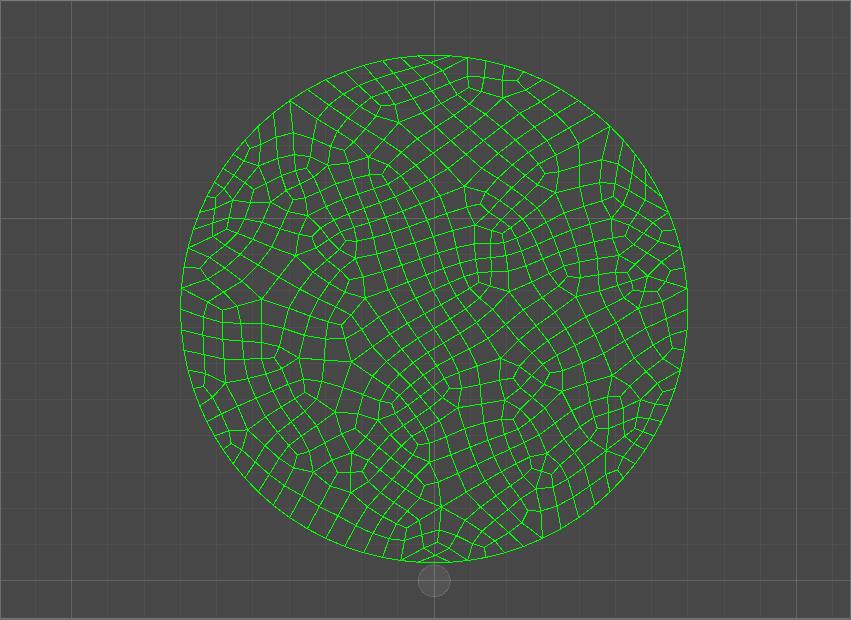
Townscaper,一款关于城镇建造的游戏。
游戏基于一张用不规则凸四边形拼接而成的平面地图,其中每个四边形虽不规则,但又“接近”正方形,适合用于城镇的搭建。
本文将用 Unity 和 C# 实现这个算法,并逐步骤解释。
算法分为如下三个步骤:
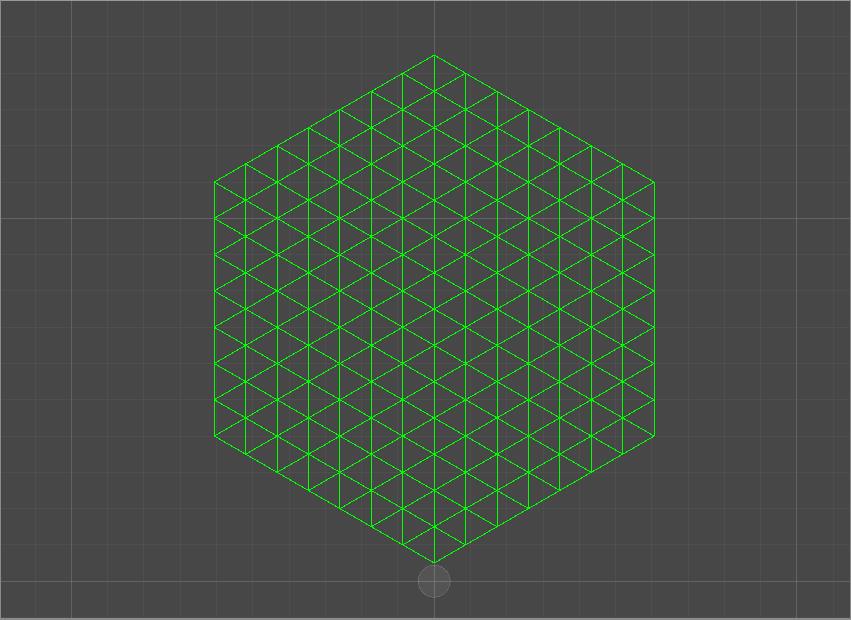
| 泊松分布的散点 | Delaunay 三角剖分 |
|---|---|
 |
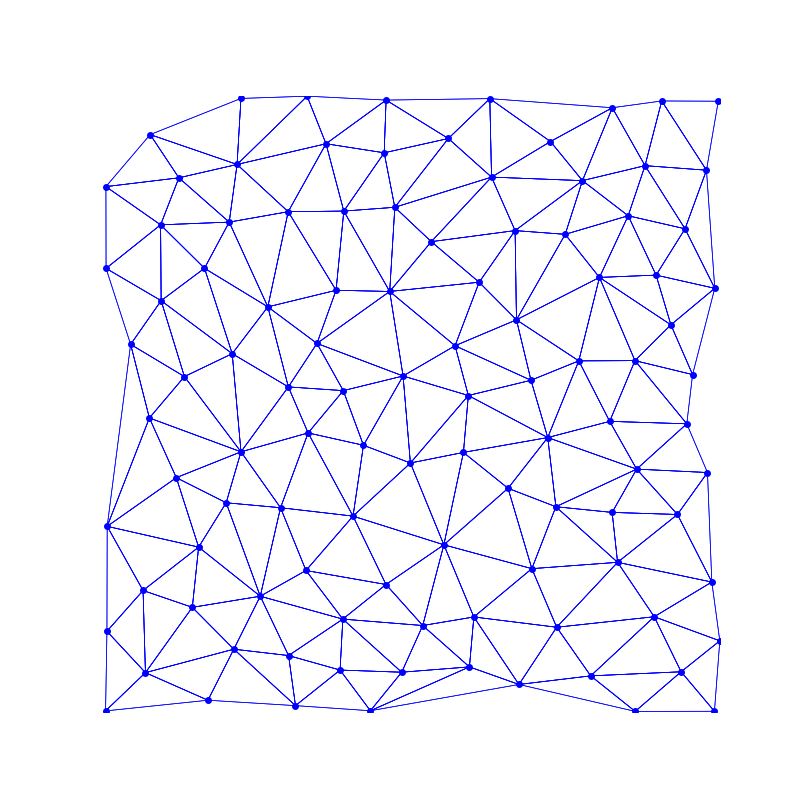 |
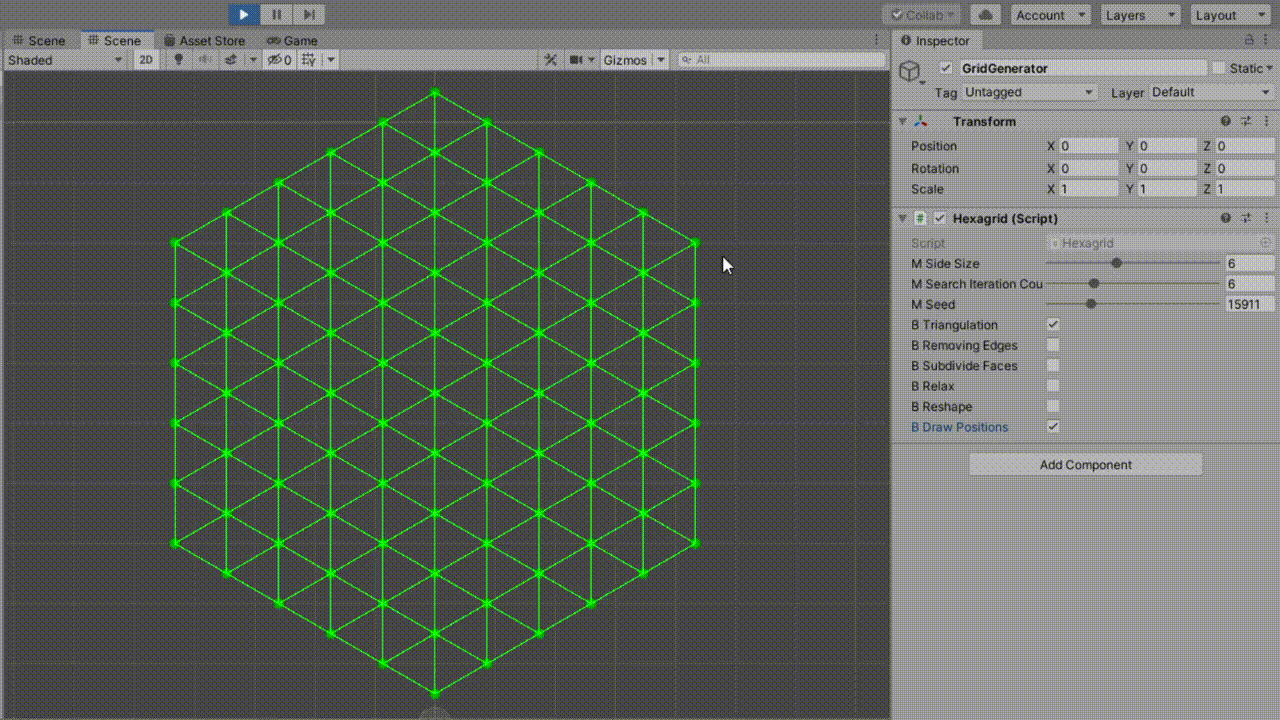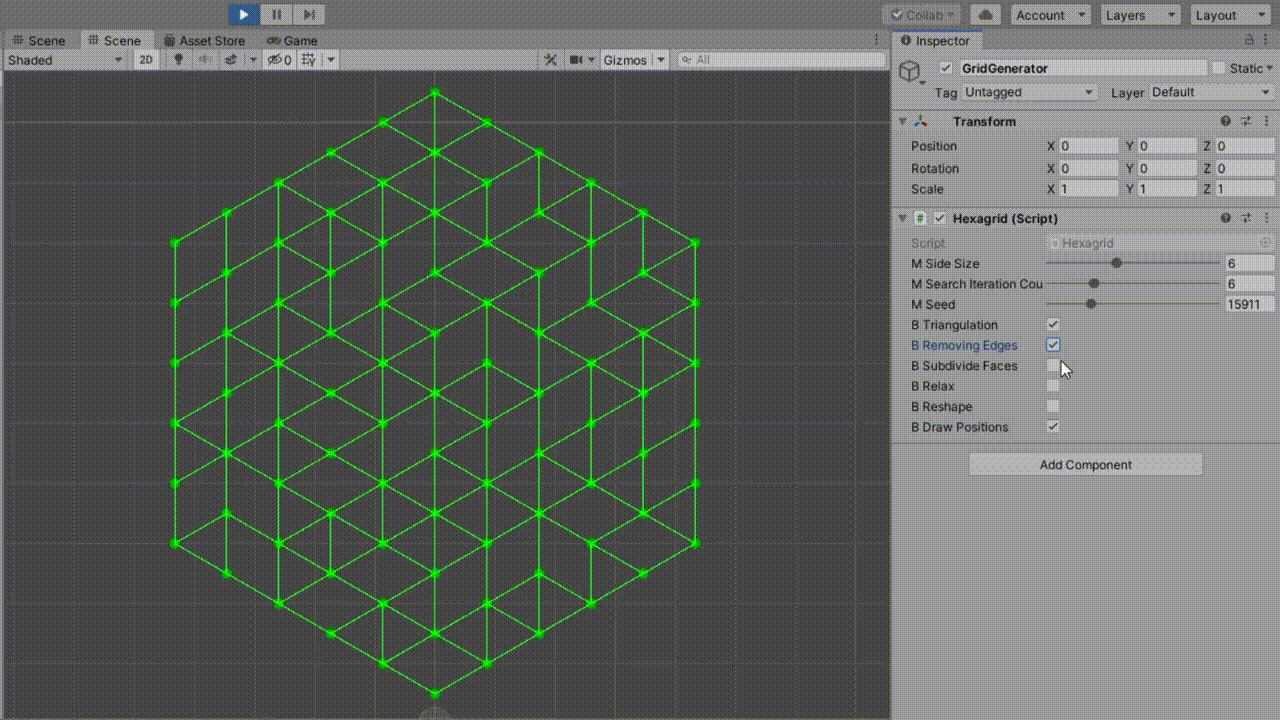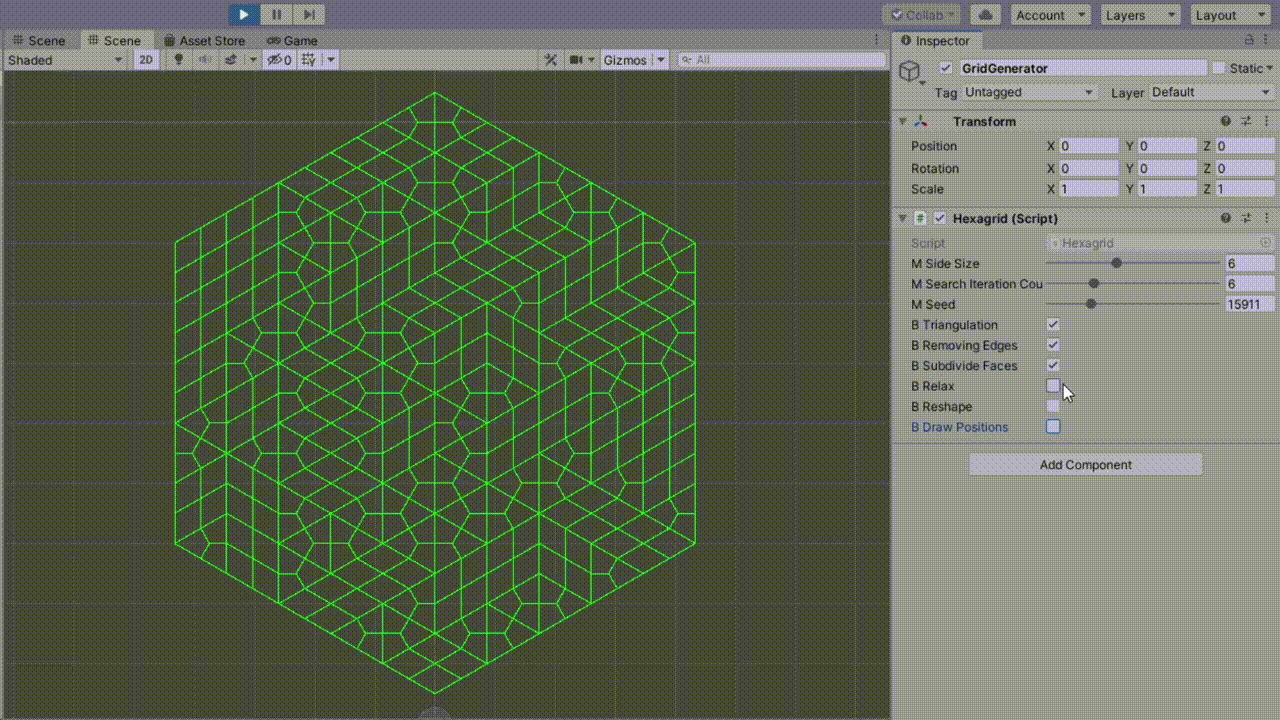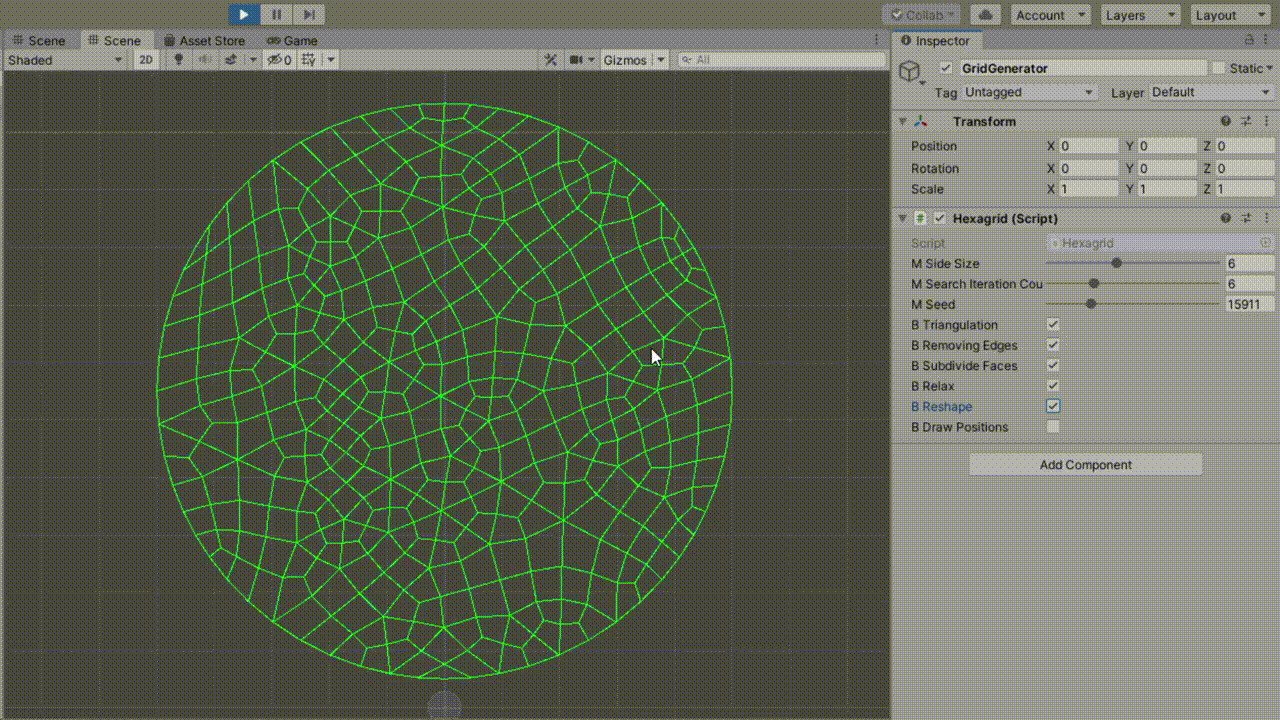
泊松分布+Delaunay 是为了获取尽量规整的三角形,
考虑到拼接无限地图的需求,此处的代码实现我们将用将 “正六边形” 三角形化的方式替代。
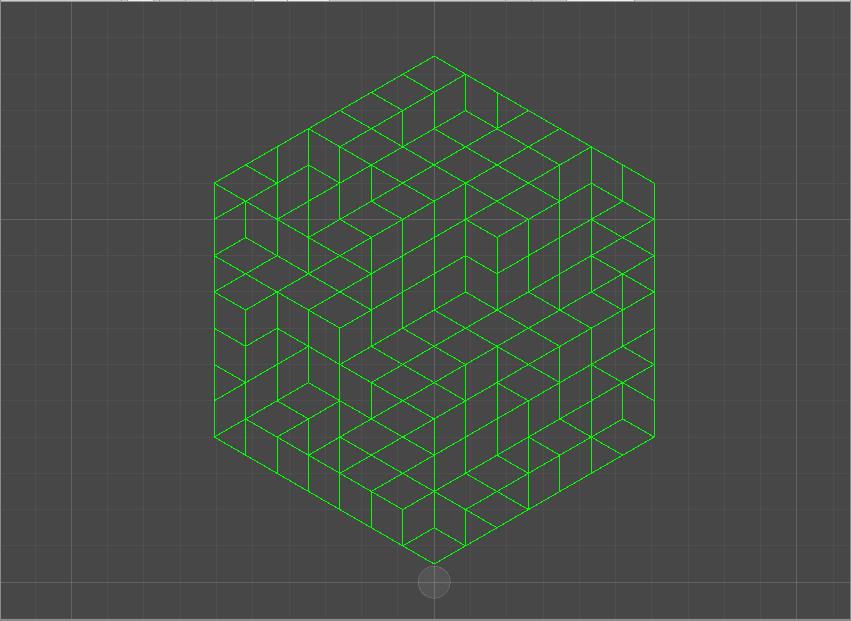
| Delaunay 三角剖分 | 剔除边后的平面 |
|---|---|
 |
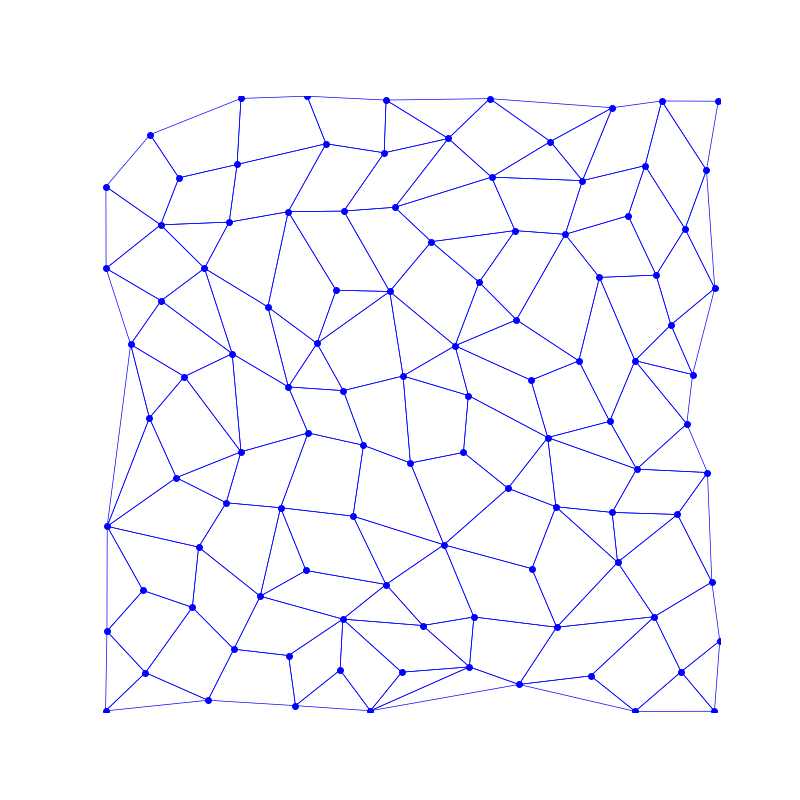 |
随机剔除三角形的边,使其和邻接三角形形成四边形。(本步骤不能保证所有三角形都被合并为四边形)
我们需要仅由具有四个边的面组成的网格。但是我们当前的网格中仍然存在一些三角形。
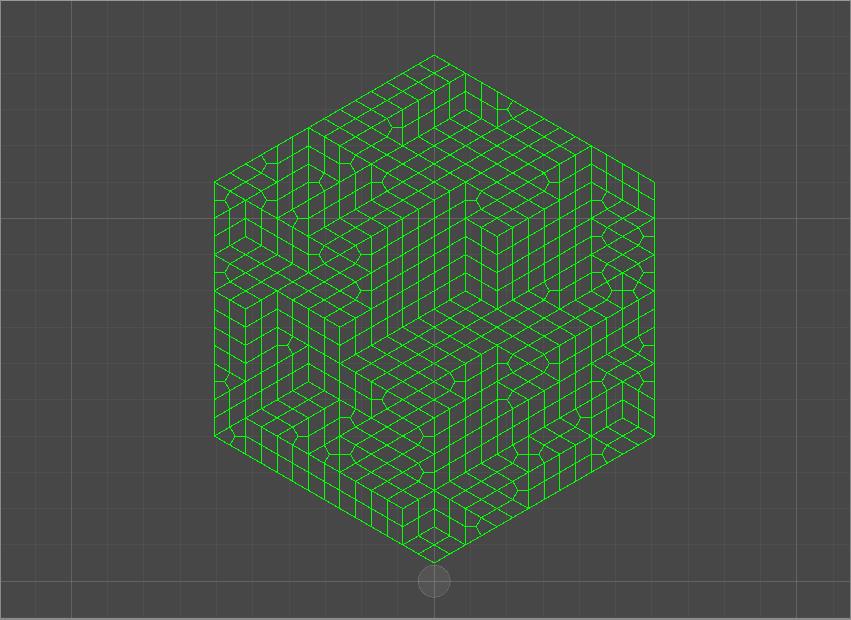
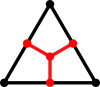
不过,三角形可以很容易地细分为三个较小的四边形。同样,现有的四边形也可以细分为四个较小的四边形。如下图所示:
| 三角形 -> 四边形 | 四边形 -> 四边形 |
|---|---|
 |
 |
通过这样做,我们最终得到一个仅由四边形组成的网格。
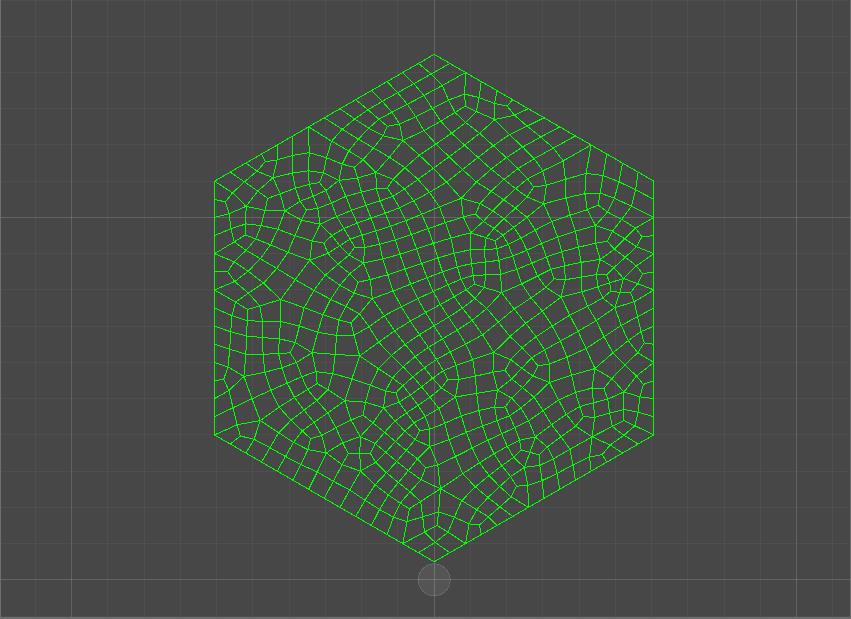
| 三角形和四边形组成的平面 | 仅由四边形组成的平面 |
|---|---|
 |
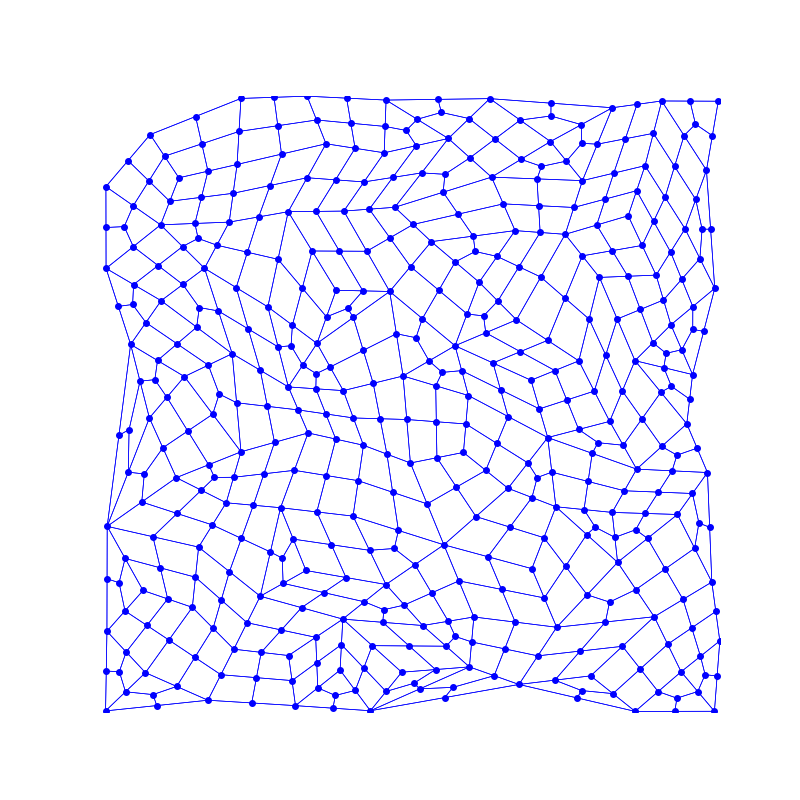 |
这一步被称为 Squaring 或 Relaxation。
目的是为了让网格看起来更加“美观”,评判标准比较主观,有多种实现方式。
我们将采用将不断迭代每个顶点,将其移向相邻顶点中心的方式实现。
新建一个 c# 脚本,派生于 MonoBehaviour,此处我们叫他 Hexagird.cs
[ExecuteInEditMode]
public class Hexagrid : MonoBehaviour
{
void Start() ...
void Update() ...
}点、三角形、四边形 的抽象,便于后续代码实现。
class Point // 点
{
public Vector2 mPosition;
public bool mSide; // 是否在六边形最外圈
};
class Triangle // 三角形
{
public int mA, mB, mC;
public bool mValid; // 用于剔除边的标记,剔除后赋值为 false
};
class Quad // 四边形
{
public int mA, mB, mC, mD;
};
class Neighbours // “点” 所邻接的其他点
{
public void Add(int i) ... // i 为邻接点索引
public int count
{
get {
return mNeighbour.Count;
}
}
public List<int> mNeighbour;
};最后给 Hexagrid 添加一些字段,用于控制生成参数,把脚本挂到场景内的一个空物体上。
[ExecuteInEditMode]
public class Hexagrid : MonoBehaviour
{
[Range(2, 12)]
public int mSideSize = 8;
[Range(1, 20)]
public int mSearchIterationCount = 12;
[Range(0, 65535)]
public int mSeed = 15911;
private int mBaseQuadCount = 0;
public bool bTriangulation = true;
public bool bRemovingEdges = false;
public bool bSubdivideFaces = false;
public bool bRelax = false;
public bool bReshape = false;
public bool bDrawPositions = false;
private List<Point> mPoints;
private List<Triangle> mTriangles;
private List<Quad> mQuads;
private Neighbours[] mNeighbours;
// 分别对应算法的四个步骤,先留空实现,慢慢补全
void Triangulation() {}
void RemovingEdges() {}
void SubdivideFaces() {}
void Relax() {}
void Reshape() {} // 额外的轮廓相形
// 绘图函数,不重要,从github把代码复制过来就行
private void DrawLine(int a, int b) ...
void OnDrawGizmos() ...
// 当参数改变时,重新初始化
private void OnValidate()
{
mPoints = new List<Point>();
mTriangles = new List<Triangle>();
mQuads = new List<Quad>();
mNeighbours = new Neighbours[0];
if (bTriangulation) {
this.Triangulation();
}
if (bTriangulation && bRemovingEdges) {
this.RemovingEdges();
}
if (bTriangulation && bRemovingEdges && bSubdivideFaces) {
this.SubdivideFaces();
}
}
// 重写 Update(),逐帧 Relax,方便看效果
void Update()
{
if (bTriangulation && bRemovingEdges && bSubdivideFaces && bRelax) {
if (bRelax) {
this.Relax();
}
if (bRelax && bReshape) {
this.Reshape();
}
}
}
}准备工作完成了,开始干正事:
void Triangulation()
{
mPoints = new List<Point>();
mTriangles = new List<Triangle>();
mQuads = new List<Quad>();
mNeighbours = new Neighbours[0];
// 将六边形内散点坐标塞进 mPoints
float sideLength = 0.5f * Mathf.Tan(Mathf.Deg2Rad * 60); // 0.5f* tanf(60deg)
for (int x = 0; x < mSideSize * 2 - 1; ++x) {
int height = (x < mSideSize) ? (mSideSize + x) : (mSideSize * 3 - 2 - x);
float deltaHeight = mSideSize - height * 0.5f;
for (int y = 0; y < height; y++) {
bool isSide = x == 0 || x == (mSideSize * 2 - 2) || y == 0 || y == height - 1;
mPoints.Add(new Point((x - mSideSize + 1) * sideLength, y + deltaHeight, isSide));
}
}
// 分别给对称轴左右生成三角形(顶点顺序不同),塞进 mTriangles
int offset = 0;
for (int x = 0; x < (mSideSize * 2 - 2); x++) {
int height = (x < mSideSize) ? (mSideSize + x) : (mSideSize * 3 - 2 - x);
if (x < mSideSize - 1) {
// left side
for (int y = 0; y < height; y++) {
mTriangles.Add(new Triangle(offset + y, offset + y + height, offset + y + height + 1));
if (y >= height - 1) {
break;
}
mTriangles.Add(new Triangle(offset + y + height + 1, offset + y + 1, offset + y));
}
}
else {
// right side
for (int y = 0; y < height - 1; y++) {
mTriangles.Add(new Triangle(offset + y, offset + y + height, offset + y + 1));
if (y >= height - 2) {
break;
}
mTriangles.Add(new Triangle(offset + y + 1, offset + y + height, offset + y + height + 1));
}
}
offset += height;
}
}现在我们得到了存储在 mPoints 里的正六边形内顶点坐标,
以及存储在 mTriangles 里的三角形 index buffer.
private int[] GetAdjacentTriangles(int triIndex); // 获取邻接的三角形索引
void RemovingEdges()
{
// triangles to quads
System.Random rand = new System.Random(mSeed);
while (true) {
int triIndex;
int searchCount = 0;
do {
triIndex = rand.Next() % mTriangles.Count;
searchCount++;
} while (searchCount < mSearchIterationCount && !mTriangles[triIndex].mValid);
if (searchCount == mSearchIterationCount) {
break;
}
int[] adjacents = GetAdjacentTriangles(triIndex);
if (adjacents.Length > 0) {
int i1 = triIndex;
int i2 = adjacents[0];
int[] indices = new int[6] {
mTriangles[i1].mA, mTriangles[i1].mB, mTriangles[i1].mC,
mTriangles[i2].mA, mTriangles[i2].mB, mTriangles[i2].mC
};
Array.Sort(indices);
int[] unique = indices.Distinct().ToArray();
Debug.Assert(unique.Length == 4);
mQuads.Add(new Quad(unique[0], unique[2], unique[3], unique[1]));
mTriangles[triIndex].mValid = false; ;
mTriangles[adjacents[0]].mValid = false;
}
}
this.mBaseQuadCount = mQuads.Count();
}随机选择三角形,获取一个与其相邻的三角形,剔除一条公用边,更新 mValid 标记。
拼接成的四边形塞进 mQuads
// 输入三角形/四边形顶点数组,和一个记录中点位置的字典
// 细分得到的顶点和四边形 index buffer 分别塞进 mPoints 和 mQuads
void Subdivide(int[] indices, Dictionary<UInt32, int> middles);
void SubdivideFaces()
{
Dictionary<UInt32, int> middles = new Dictionary<UInt32, int>();
// quads to 4 quads
for (int i = 0; i < mBaseQuadCount; i++) {
var quad = mQuads[i];
int[] indices = new int[4] {
quad.mA, quad.mB, quad.mC, quad.mD
};
this.Subdivide(indices, middles);
}
// triangles to quads
foreach (var triangle in mTriangles) {
if (triangle.mValid) {
int[] indices = new int[3] {
triangle.mA, triangle.mB, triangle.mC
};
this.Subdivide(indices, middles);
}
}
}void Relax()
{
mNeighbours = new Neighbours[mPoints.Count];
for (int i = 0; i < mPoints.Count; ++i) {
mNeighbours[i] = new Neighbours();
}
for (int i = mBaseQuadCount; i < mQuads.Count(); ++i) {
var quad = mQuads[i];
int[] indices = new int[4] {
quad.mA, quad.mB, quad.mC, quad.mD
};
for (int j = 0; j < 4; j++) {
int index1 = indices[j];
int index2 = indices[(j + 1) & 3];
{
var neighbour = mNeighbours[index1];
// check
bool good = true;
for (int k = 0; k < neighbour.count; k++) {
if (neighbour.mNeighbour[k] == index2) {
good = false;
break;
}
}
if (good) {
Debug.Assert(neighbour.count < 6);
neighbour.Add(index2);
}
}
{
var neighbour = mNeighbours[index2];
// check
bool good = true;
for (int k = 0; k < neighbour.count; k++) {
if (neighbour.mNeighbour[k] == index1) {
good = false;
break;
}
}
if (good) {
Debug.Assert(neighbour.count < 6);
neighbour.Add(index1);
}
}
}
}
for (int i = 0; i < mPoints.Count; i++) {
if (mPoints[i].mSide) {
continue;
}
var neighbour = mNeighbours[i];
Vector2 sum = Vector2.zero;
for (int j = 0; j < neighbour.count; j++) {
sum += mPoints[neighbour.mNeighbour[j]].mPosition;
}
sum /= (float)neighbour.count;
mPoints[i].mPosition = sum;
}
}void Reshape()
{
float radius = mSideSize - 1.0f;
Vector2 center = new Vector2(0, (mSideSize * 2 - 1) * 0.5f);
foreach (var point in mPoints) {
if (!point.mSide) {
continue;
}
Vector2 D = point.mPosition - center;
float distance = radius - Mathf.Sqrt(D.x * D.x + D.y * D.y);
point.mPosition += (D * distance) * 0.1f;
}
}