Multi-Goal A-star

This repo contains code to search for multiple goals with heterogenous values using a 3D A-star discrete planner. The majority of the code is written in C++ with Python bindings. This planner was used in the paper Map-Based Planning for Small Unmanned Aircraft Rooftop Landing

What do you mean by discrete?

The map provided should be a 3D voxel grid(i, j, k), a 3D NumPy array, which the planner searches. A cell with the value 0.0 is considered free space. A cell with the value 1.0 is considered an obstacle and cannot be traversed (this value is configurable). Values between 0.0 and 1.0 can be traversed but with a penalty (penalty weight is configurable).

What do you mean by multiple goals with heterogenous values?

A normal A-star planner has a start location and one goal. This Multi-Goal planner allows you to provide multiple goal cells each having different values. Goals with lower values are more desirable. This planner will try to find the optimal goal and path which minimizes an objective function. It must be understood that the planner doesn't just find a path. It finds the one goal and the corresponding optimal path that minimizes some larger objective function.

What is the larger objective function?

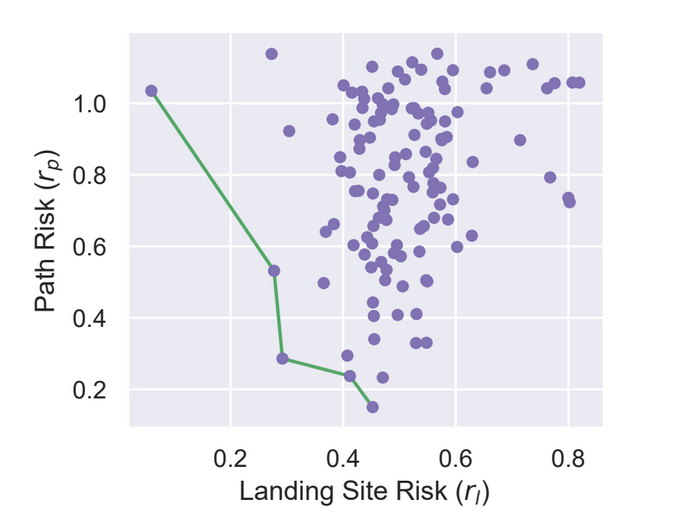
The objective function is the minimization of total risk ($r_t$), which is the combination of path risk ($r_p$) and goal risk $r_g$. In my research the goals were landing sites, therefore I called the latter landing site risk $r_l$. Below is an excerpt from my paper that discusses this trade-off between objectives:

The figure below shows an example Pareto frontier that minimizes two objectives: landing
site risk and path risk. Each purple dot represents a landing site. The x-axis represents
landing site risk and the y-axis represents path risk to that site. The green line
connects five points on the Pareto frontier, the set of non-dominated landing sites
for which any improvement in one objective results in a negative trade-off in the other.
Each of these five landing sites is “optimal”, and a quantifiable relationship between
each objective must be constructed to select a final choice. A linear weighting scheme
is used for these purposes

$$ r_t = w_l \cdot r_l + w_p · r_p $$

Given the weighting between the two objectives, one of the purple dots on the green line is considered the "best" goal/path pair and will have minimum total risk. Here's the kicker though: you do not know the path risk until you do path planning. However, path planning is very expensive. PyMultiAStar will search for the optimal goal/path such that we minimize our expensive path planning procedures, often only needing to perform path planning 1-3 times on average.

How do you minimize path planning? How do you know when to stop searching?

We first sort the goals by their minimum total risk $r_{t,min}$ where

$$r_{t,min} = w_{g} \cdot r_{g} + w_p \cdot h(\mathbf{start}, \mathbf{goal}) / R$$

where $h$ is an admissible heuristic and $R$ is a normalizing constant. Basically, we are bounding the minimum path distance which in turn bounds total risk. $R$ is usually the largest distance permissible during path planning. This entire list is very cheap to compute and sort.

The first goal in this sorted list is the most likely to be the lowest total risk, but we don't know until we do path planning. After path planning to this goal, we can determine the true path risk and calculate the total risk. If the goal's total risk is less than the next goal's minimum total risk, we can guarantee we found the optimal solution to our objective function. We can stop searching!

What precisely are these objectives and where are the details of the planner?

See the following sections in the paper linked above:

Definition of Path Cost: Section 1.3.2, Equations 1.6-1.8
Definition of Path Risk: Section 1.5, Equation 1.17
Definition of Landing Site (Goal) Risk: Section 1.4.4, Equation 1.9. This can be defined as anything for your specific problem.
Definition of Total Risk: Section 1.6.2, Equation 1.18.
Proof of Planner: Section 1.6.3

Install

Binary Wheels are provided for you on PyPi:

Discrete Multi-Goal Planner - pip install pymultiastar - This exposes the class PyMultiAStar
1. This planner only knows about Voxel Grid to traverse.
Geographically Aware Planner - pip install pymultiastar[geo] - This also exposes the class GeoPlanner
1. This is a geographically aware wrapper around PyMultiAStar. You give a georeferenced voxel map and start conditions in GPS and landing sites in GPS and it will do the conversions between GPS to voxel cell for you.

How to use

Below are some examples:

run_simple_world_3d.py. Shows a very simple example of a small 3D world with multiple goals.
run_maze_2d.py - Demonstrates that 2D A-star path planning is a subset of the Multi-Goal Planner. It loads a 2D image of a maze as a single slice in a 3D world and has only 1 goal.
run_scenarios.py - Shows how to use the GeoPlanner and plan in a 3D world.

JeremyBYU/pymultiastar

Multi-Goal A-star

Install

How to use