Main Status:

Develop Status:

Mission: To make nested sampling faster, easier, and more powerful

What is it?

JAXNS is:

a simple and powerful probabilistic programming framework using nested sampling as the engine;
coded in JAX in a manner that allows lowering the entire inference algorithm to XLA primitives, which are JIT-compiled for high performance;
continuously improving on its mission of making nested sampling faster, easier, and more powerful; and
citable, use the (old) pre-print here.

What can you do with JAXNS?

Compute the Bayesian evidence of a model or hypothesis (the ultimate scientific method);
Produce high-quality samples from the posterior distribution;
Easily handle degenerate difficult multi-modal posteriors;
Model both discrete and continuous priors and likelihoods;
Encode complex constraints on the prior space;
Easily embed neural networks or any other ML model in the likelihood/prior;

JAXNS Probabilistic Programming Framework

JAXNS provides a powerful JAX-based probabilistic programming framework, which allows you to define probabilistic models easily, and use them for advanced purposes. Probabilistic models can have both Bayesian and parameterised variables. Bayesian variables are random variables, and are sampled from a prior distribution. Parameterised variables are point-wise representations of a prior distribution, and are thus not random. Associated with them is the log-probability of the prior distribution at that point.

Let's break apart an example of a simple probabilistic model. Note, this example can also be followed in docs/examples/intro_example.ipynb.

Defining a probabilistic model

Prior models are functions that produce generators of Prior objects. The function must eventually return the inputs to the likelihood function. The returned values of a yielded Prior is a simple JAX array, i.e. you can do anything you want to it with JAX ops. The rules of static programming apply, i.e. you cannot dynamically allocate arrays.

JAXNS makes use of the Tensorflow Probability library for defining prior distributions, thus you can use almost any of the TFP distributions. You can also use any of the TFP bijectors to define transformed distributions.

Distributions do have some requirements to be valid for use in JAXNS.

They must have a quantile function, i.e. dist.quantile(dist.cdf(x)) == x.
They must have a log_prob method that returns the log-probability of the distribution at a given value.

Most of the TFP distributions satisfy these requirements.

JAXNS has some special priors defined that can't be defined from TFP, see jaxns.framework.special_priors. You can always request more if you need them.

Prior variables may be named but don't have to be. If they are named then they can be collected later via a transformation, otherwise they are deemed hidden variables.

The output values of prior models are the inputs to the likelihood function. They can be PyTree's, e.g. typing.NamedTuple's.

Finally, priors can become point-wise estimates of the prior distribution, by calling parametrised(). This turns a Bayesian variable into a parameterised variable, e.g. one which can be used in optimisation.

import jax
import tensorflow_probability.substrates.jax as tfp

tfpd = tfp.distributions

from jaxns.framework.model import Model
from jaxns.framework.prior import Prior


def prior_model():
    mu = yield Prior(tfpd.Normal(loc=0., scale=1.))
    # Let's make sigma a parameterised variable
    sigma = yield Prior(tfpd.Exponential(rate=1.), name='sigma').parametrised()
    x = yield Prior(tfpd.Cauchy(loc=mu, scale=sigma), name='x')
    uncert = yield Prior(tfpd.Exponential(rate=1.), name='uncert')
    return x, uncert


def log_likelihood(x, uncert):
    return tfpd.Normal(loc=0., scale=uncert).log_prob(x)


model = Model(prior_model=prior_model, log_likelihood=log_likelihood)

# You can sanity check the model (always a good idea when exploring)
model.sanity_check(key=jax.random.PRNGKey(0), S=100)

# The size of the Bayesian part of the prior space is `model.U_ndims`.

Sampling and transforming variables

There are two spaces of samples:

U-space: samples in base measure space, and is dimensionless, or rather has units of probability.
X-space: samples in the space of the model, and has units of the prior variable.

# Sample the prior in U-space (base measure)
U = model.sample_U(key=jax.random.PRNGKey(0))
# Transform to X-space
X = model.transform(U=U)
# Only named Bayesian prior variables are returned, the rest are treated as hidden variables.
assert set(X.keys()) == {'x', 'uncert'}

# Get the return value of the prior model, i.e. the input to the likelihood
x_sample, uncert_sample = model.prepare_input(U=U)

Computing log-probabilities

All computations are based on the U-space variables.

# Evaluate different parts of the model
log_prob_prior = model.log_prob_prior(U)
log_prob_likelihood = model.log_prob_likelihood(U, allow_nan=False)
log_prob_joint = model.log_prob_joint(U, allow_nan=False)

Computing gradients of the joint probability w.r.t. parameters

init_params = model.params


def log_prob_joint_fn(params, U):
    # Calling model with params returns a new model with the params set
    return model(params).log_prob_joint(U, allow_nan=False)


value, grad = jax.value_and_grad(log_prob_joint_fn)(init_params, U)

Nested Sampling Engine

Given a probabilistic model, JAXNS can perform nested sampling on it. This allows computing the Bayesian evidence and posterior samples.

from jaxns import NestedSampler

ns = NestedSampler(model=model, max_samples=1e5)

# Run the sampler
termination_reason, state = ns(jax.random.PRNGKey(42))
# Get the results
results = ns.to_results(termination_reason=termination_reason, state=state)

To AOT or JIT-compile the sampler

# Ahead of time compilation (sometimes useful)
ns_aot = jax.jit(ns).lower(jax.random.PRNGKey(42)).compile()

# Just-in-time compilation (usually useful)
ns_jit = jax.jit(ns)

You can inspect the results, and plot them.

from jaxns import summary, plot_diagnostics, plot_cornerplot, save_results, load_results

# Optionally save the results to file
save_results(results, 'results.json')
# To load the results back use this
results = load_results('results.json')

summary(results)
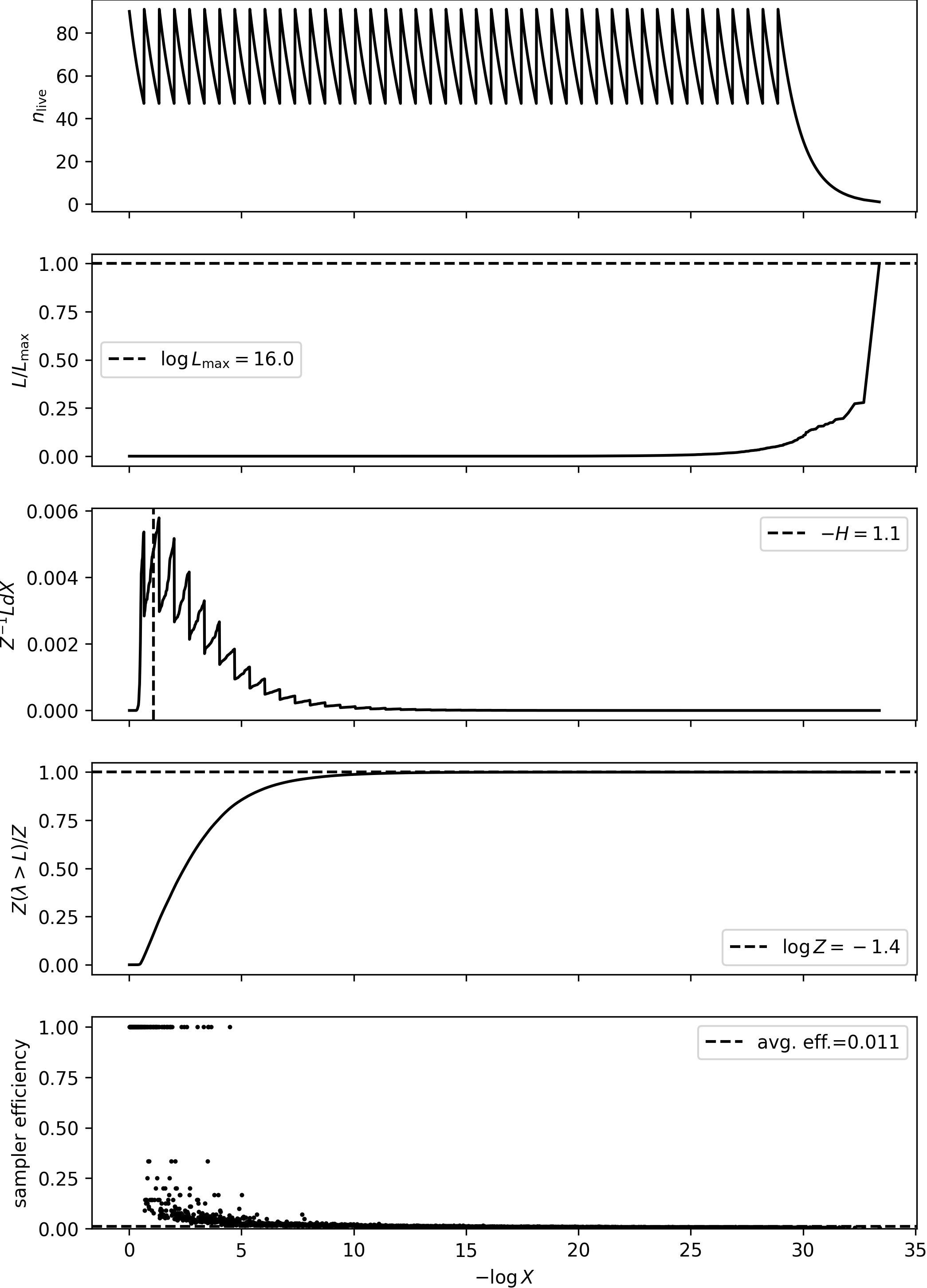
plot_diagnostics(results)
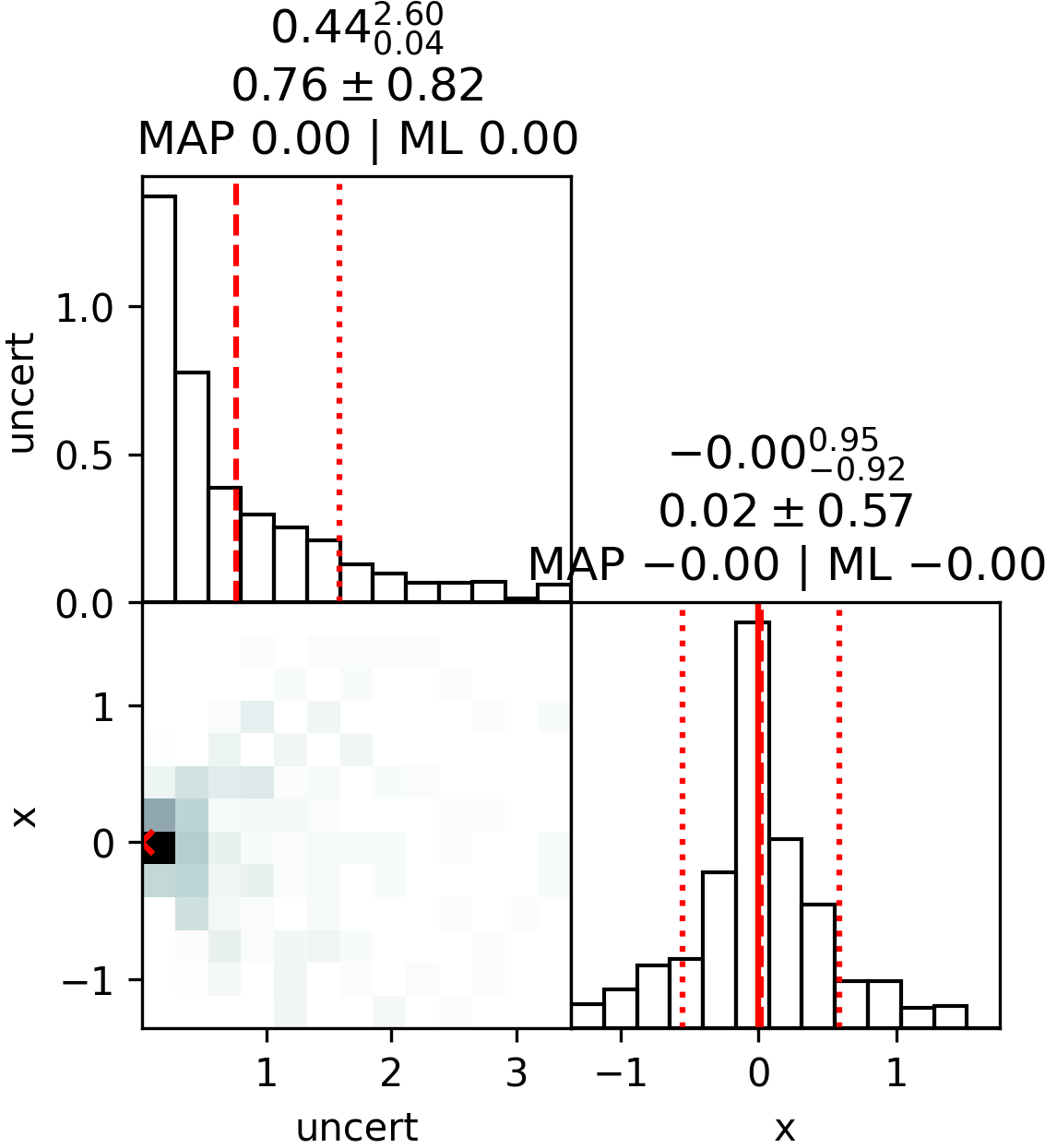
plot_cornerplot(results)

Output:

--------
Termination Conditions:
Small remaining evidence
--------
likelihood evals: 149918
samples: 3780
phantom samples: 1710
likelihood evals / sample: 39.7
phantom fraction (%): 45.2%
--------
logZ=-1.65 +- 0.15
H=-1.13
ESS=132
--------
uncert: mean +- std.dev. | 10%ile / 50%ile / 90%ile | MAP est. | max(L) est.
uncert: 0.68 +- 0.58 | 0.13 / 0.48 / 1.37 | 0.0 | 0.0
--------
x: mean +- std.dev. | 10%ile / 50%ile / 90%ile | MAP est. | max(L) est.
x: 0.07 +- 0.62 | -0.57 / 0.06 / 0.73 | 0.0 | 0.0
--------

Using the posterior samples

Nested sampling produces weighted posterior samples. To use for most use cases, you can simply resample (with replacement).

from jaxns import resample

samples = resample(
    key=jax.random.PRNGKey(0),
    samples=results.samples,
    log_weights=results.log_dp_mean,
    S=1000,
    replace=True
)

Maximising the evidence

The Bayesian evidence is the ultimate model selection density, and choosing a model that maximises the evidence is the best way to select a model. We can use the evidence maximisation algorithm to optimise the parametrised variables of the model, in the manner that maximises the evidence. Below EvidenceMaximisation does this for the model we defined above, where the parametrised variables are automatically constrained to be in the right range, and numerical stability is ensured with proper scaling.

We see that the evidence maximisation chooses a sigma the is very small.

from jaxns.experimental import EvidenceMaximisation

# Let's train the sigma parameter to maximise the evidence

em = EvidenceMaximisation(model)
results, params = em.train(num_steps=5)

summary(results, with_parametrised=True)

Output:

--------
Termination Conditions:
Small remaining evidence
--------
likelihood evals: 72466
samples: 1440
phantom samples: 0
likelihood evals / sample: 50.3
phantom fraction (%): 0.0%
--------
logZ=-1.119 +- 0.098
H=-0.93
ESS=241
--------
sigma: mean +- std.dev. | 10%ile / 50%ile / 90%ile | MAP est. | max(L) est.
sigma: 5.40077599e-05 +- 3.6e-12 | 5.40077563e-05 / 5.40077563e-05 / 5.40077563e-05 | 5.40077563e-05 | 5.40077563e-05
--------
uncert: mean +- std.dev. | 10%ile / 50%ile / 90%ile | MAP est. | max(L) est.
uncert: 0.6 +- 0.54 | 0.05 / 0.45 / 1.37 | 0.0 | 0.0
--------
x: mean +- std.dev. | 10%ile / 50%ile / 90%ile | MAP est. | max(L) est.
x: 0.01 +- 0.56 | -0.6 / -0.0 / 0.69 | 0.0 | -0.0
--------

Documentation

You can read the documentation here. In addition, JAXNS is partially described in the original paper, as well as the paper on Phantom-Powered Nested Sampling paper.

Install

Notes:

JAXNS requires >= Python 3.9. It is always highly recommended to use the latest version of Python.
It is always highly recommended to use a unique virtual environment for each project. To use miniconda, ensure it is installed on your system, then run the following commands:

# To create a new env, if necessary
conda create -n jaxns_py python=3.12
conda activate jaxns_py

For end users

Install directly from PyPi,

pip install jaxns

For development

Clone repo git clone https://www.github.com/JoshuaAlbert/jaxns.git, and install:

cd jaxns
pip install -r requirements.txt
pip install -r requirements-tests.txt
pip install -r requirements-examples.txt
pip install .

Getting help and contributing examples

Do you have a neat Bayesian problem, and want to solve it with JAXNS? I'm really encourage anyone in either the scientific community or industry to get involved and join the discussion forum. Please use the github discussion forum for getting help, or contributing examples/neat use cases.

Quick start

Checkout the examples here.

Caveats

The caveat is that you need to be able to define your likelihood function with JAX. UPDATE: now you can just use the @jaxify_likelihood decorator to run with arbitrary pythonic likelihoods.

Speed test comparison with other nested sampling packages

JAXNS is really fast because it uses JAX. JAXNS is much faster than PolyChord, MultiNEST, and dynesty, typically achieving two to three orders of magnitude improvement in run time, for models with cheap likelihood evaluations. This is shown in (https://arxiv.org/abs/2012.15286).

Recently JAXNS has implemented Phantom-Powered Nested Sampling, which helps for parameter inference. This is shown in (https://arxiv.org/abs/2312.11330).

Note on performance with parallelisation and GPUS

To use parallel computing, you can simply pass devices to the NestedSampler constructor. This will distributed sampling over the devices. To use GPUs you can pass jax.devices('gpu') to the devices argument. You can also se all your CPUs by placing os.environ["XLA_FLAGS"] = f"--xla_force_host_platform_device_count={os.cpu_count()}" before importing JAXNS.

Change Log

7 Dec, 2024 -- JAXNS 2.6.7 released. Fix pip dependencies install.

13 Nov, 2024 -- JAXNS 2.6.6 released. Minor improvements to plotting.

9 Nov, 2024 -- JAXNS 2.6.5 released. Added gradient guided nested sampling. Removed num_parallel_workers in favour devices.

4 Nov, 2024 -- JAXNS 2.6.4 released. Resolved bias when using phantom points.

1 Oct, 2024 -- JAXNS 2.6.3 released. Enable pytrees in context.

25 Sep, 2024 -- JAXNS 2.6.2 released. Fixed some important (not so edge) cases. Made faster. Handle no seed scenarios.

24 Sep, 2024 -- JAXNS 2.6.1 released. Sharded parallel JAXNS. Rewrite of internals to support sharded parallelisation.

20 Aug, 2024 -- JAXNS 2.6.0 released. Removed haiku dependency. Implemented our own context. jaxns.framework.context.convert_external_params enables interfacing with any external NN libary.

24 Jul, 2024 -- JAXNS 2.5.3 released. Replacing framework U-space with W-space. Maintained external API in U space.

23 Jul, 2024 -- JAXNS 2.5.2 released. Added explicit density prior. Sped up parametrisation. Scan associative implemented.

27 May, 2024 -- JAXS 2.5.1 released. Fixed minor accuracy degradation introduced in 2.4.13.

15 May, 2024 -- JAXNS 2.5.0 released. Added ability to handle non-JAX likelihoods, e.g. if you have a simulation framework with python bindings you can now use it for likelihoods in JAXNS. Small performance improvements.

22 Apr, 2024 -- JAXNS 2.4.13 released. Fixes bug where slice sampling not invariant to monotonic transforms of likelihood.

20 Mar, 2024 -- JAXNS 2.4.12 released. Minor bug fixes, and readability improvements. Added Empirical special prior.

5 Mar, 2024 -- JAXNS 2.4.11/b released. Add random_init to parametrised variables. Enable special priors to be parametrised.

23 Feb, 2024 -- JAXNS 2.4.10 released. Hotfix for import error.

21 Feb, 2024 -- JAXNS 2.4.9 released. Minor improvements to some priors, and bug fixes.

31 Jan, 2024 -- JAXNS 2.4.8 released. Improved global optimisation performance using gradient slicing. Improved evidence maximisation.

25 Jan, 2024 -- JAXNS 2.4.6/7 released. Added logging. Use L-BFGS for Evidence Maximisation M-step. Fix bug in finetune.

24 Jan, 2024 -- JAXNS 2.4.5 released. Gradient based finetuning global optimisation using L-BFGS. Added ability to simulate prior models without bulding model (for data generation.)

15 Jan, 2024 -- JAXNS 2.4.4 released. Fix performance issue for larger max_samples. Fixed bug in termination conditions. Improved parallel performance.

10 Jan, 2024 -- JAXNS 2.4.2/3 released. Another performance boost, and experimental global optimiser.

9 Jan, 2024 -- JAXNS 2.4.1 released. Improve performance slightly for larger max_samples, still a performance issue.

8 Jan, 2024 -- JAXNS 2.4.0 released. Python 3.9+ becomes supported. Migrate parametrised models to stable. All models are now default able to be parametrised, so you can use hk.Parameter anywhere in the model.

21 Dec, 2023 -- JAXNS 2.3.4 released. Correction for ESS and logZ uncert. parameter_estimation mode.

20 Dec, 2023 -- JAXNS 2.3.2/3 released. Improved default parameters. difficult_model mode. Improve plotting.

18 Dec, 2023 -- JAXNS 2.3.1 released. Paper open science release. Default parameters from paper.

11 Dec, 2023 -- JAXNS 2.3.0 released. Release of Phantom-Powered Nested Sampling algorithm.

5 Oct, 2023 -- JAXNS 2.2.6 released. Minor update to evidence maximisation.

3 Oct, 2023 -- JAXNS 2.2.5 released. Parametrised priors, and evidence maximisation added.

24 Sept, 2023 -- JAXNS 2.2.4 released. Add marginalising from saved U samples.

28 July, 2023 -- JAXNS 2.2.3 released. Bug fix for singular priors.

26 June, 2023 -- JAXNS 2.2.1 released. Multi-ellipsoidal sampler added back in. Adaptive refinement disabled, as a bias has been detected in it.

15 June, 2023 -- JAXNS 2.2.0 released. Added support to allow TFP bijectors to defined transformed distributions. Other minor improvements.

15 April, 2023 -- JAXNS 2.1.0 released. pmap used on outer-most loops allowing efficient device-device communication during parallel runs.

8 March, 2023 -- JAXNS 2.0.1 released. Changed how we're doing annotations to support python 3.8 again.

3 January, 2023 -- JAXNS 2.0 released. Complete overhaul of components. New way to build models.

5 August, 2022 -- JAXNS 1.1.1 released. Pytree shaped priors.

2 June, 2022 -- JAXNS 1.1.0 released. Dynamic sampling takes advantage of adaptive refinement. Parallelisation. Bayesian opt and global opt modules.

30 May, 2022 -- JAXNS 1.0.1 released. Improvements to speed, parallelisation, and structure of code.

9 April, 2022 -- JAXNS 1.0.0 released. Parallel sampling, dynamic search, and adaptive refinement. Global optimiser released.

2 Jun, 2021 -- JAXNS 0.0.7 released.

13 May, 2021 -- JAXNS 0.0.6 released.

8 Mar, 2021 -- JAXNS 0.0.5 released.

8 Mar, 2021 -- JAXNS 0.0.4 released.

7 Mar, 2021 -- JAXNS 0.0.3 released.

28 Feb, 2021 -- JAXNS 0.0.2 released.

28 Feb, 2021 -- JAXNS 0.0.1 released.

1 January, 2021 -- Paper submitted

Joshuaalbert/jaxns