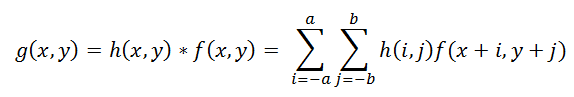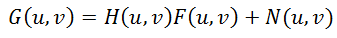Recover blurry images using Weiner deconvolution of an image with user-defined point spread function (PSF)
How use?
python wiener_deconvolution.py <image_input>Use sliders to adjust PSF paramitiers:
-angle in degrees
-diameter object PSF
-SNR - signal/noise ratio in db
Keys:
SPACE - switch btw linear/cirular PSF
ESC - exit
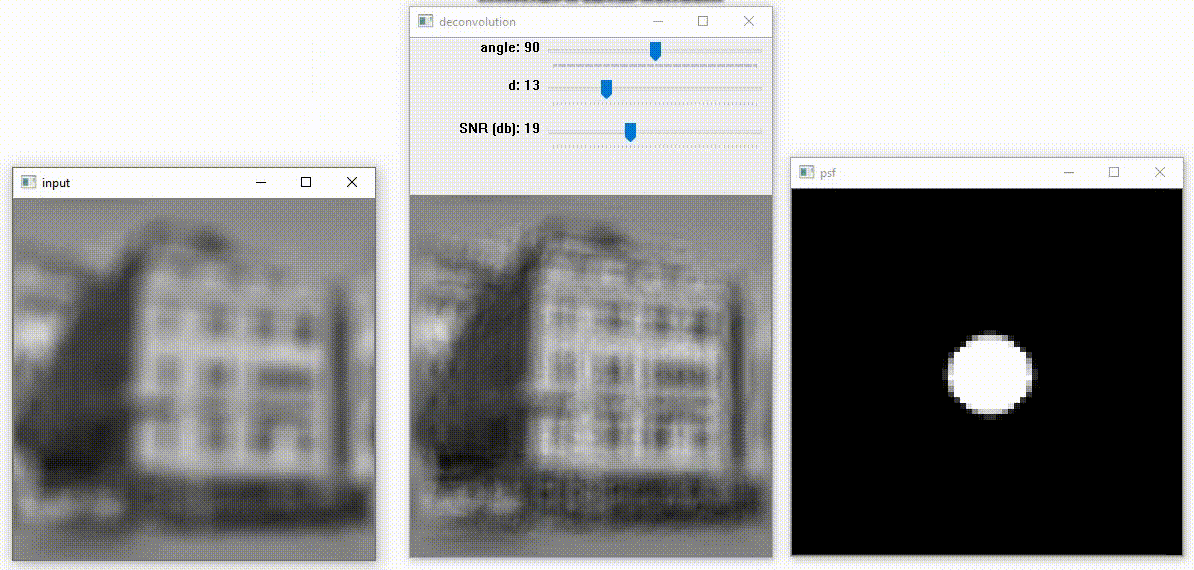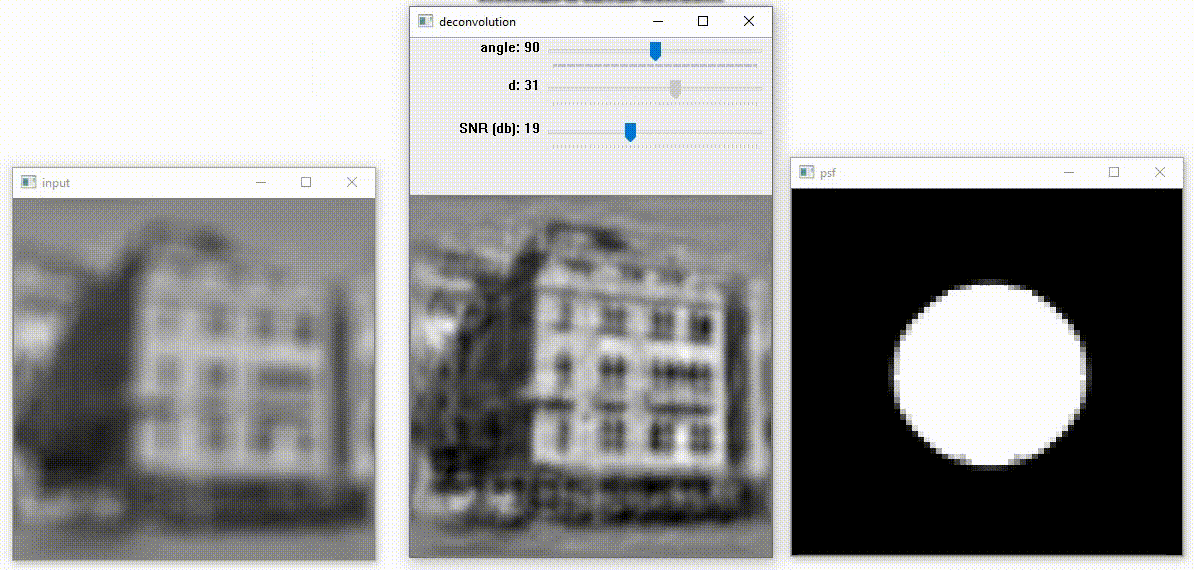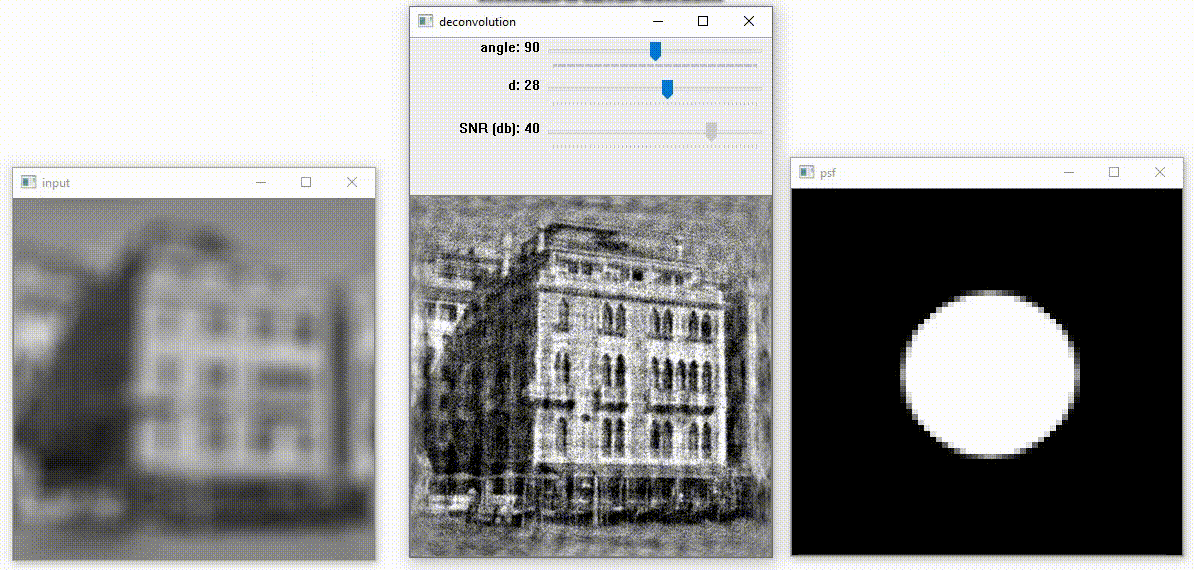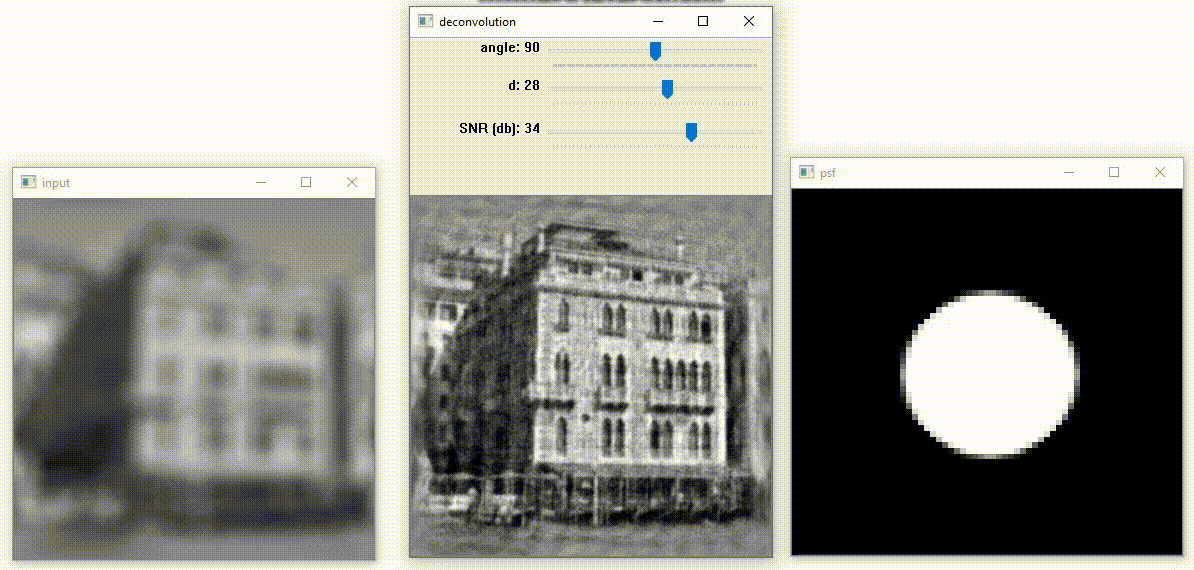
Example № 1 witn cirular PSF
Example № 2 witn linear PSF
Восстановление искаженных изображений является одной из наиболее интересных и важных проблем в задачах обработки изображений – как с теоретической, так и с практической точек зрения.
Помимо таких вещей как шум, неправильная экспозиция, дисторсия есть и более серьезные проблемы:
- размытие из-за неправильного фокуса
- смаз – дефекты
Не стоит отчаиваться, если мы видим такие изображения, все дело в том, что наша информация не теряется где-то, а просто перераспределяется по некоторому закону и может быть однозначно восстановлена с некоторыми оговорками. Исключение составляет лишь края изображения шириной в радиус размытия – там полноценное восстановление невозможно.
Будем рассматривать только полутоновые черно-белые изображения в предположении, что для обработки полноцветного изображения достаточно повторить все необходимые шаги для каждого из цветовых каналов RGB.
Пусть:
-f(x, y) – исходное неискаженное изображение
-h(x, y) – искажающая функция
-n(x, y) – аддитивный шум
-g(x, y) – результат искажения, т.е. то, что мы наблюдаем в результате (смазанное или расфокусированное изображение)
Сформулируем модель процесса искажения следующим образом:
g(x, y) = h(x, y) \* f(x, y) + n(x, y)
Задача восстановления искаженного изображения заключается в нахождении наилучшего приближения f'(x, y) исходного изображения
В процессе искажения каждый пиксель исходного изображения превращается в пятно для случая расфокусировки и в отрезок для случая простого смаза.
Что такое h(x,y)?
То, по какому закону размазывается или собирается один пиксель и называется функцией искажения. Другие синонимы – PSF (Point spread function, т.е. функция распределения точки), ядро искажающего оператора, kernel и другие.
Операция применения искажающей функции к другой функции (к изображению, в данном случае) называется сверткой (convolution), т.е. некоторая область исходного изображения сворачивается в один пиксель искаженного изображения. Обозначается через оператор «*». Математически для изображения f с размерами M x N и искажающей функции h c размерами m x n это записывается так:
Осталось рассмотреть последнее слагаемое, отвечающее за шум, n(x, y) в формуле. Причины шума в цифровых сенсорах могут быть самыми разными, но основные это – тепловые колебания и темновые токи. На величину шума также влияет ряд факторов, таких как значение ISO, тип матрицы, размер пикселя, температура, электромагнитные наводки и пр. В большинстве случаев шум является Гауссовым (который задается двумя параметрами – средним и дисперсией), а также является аддитивным, не коррелирует с изображением и не зависит координат пикселя.
На помощь к нам приходит преобразование Фурье. Есть такая теорема о свертке, которая гласит, что операция свертки в пространственной области эквивалентна обычному умножению в частотной области (причем умножение поэлементное, а не матричное).
Соответственно, операция обратная свертке эквивалентна делению в частотной области, т.е. это можно записать как: 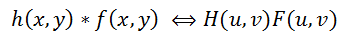
Где H(u, v), F(u, v) – Фурье-образы соответствующих функций. Значит процесс искажения из формулы (1) можно переписать в частотной области как:
Как в этом случае избавиться от шума чтобы выполнить обратную свертку, деконволюцию?
Есть подходы, которые учитывают наличие шума на изображении – один из самых известных и самых первых, это фильтр Винера (Wiener). Он рассматривает изображение и шум как случайные процессы и находит такую оценку f' для неискаженного изображения f, чтобы среднеквадратическое отклонение этих величин было минимальным.
- Считываем изображение, нормализуем, делаем размытие краев, делаем преобразования Фурье.
img = cv2.imread(fn, 0)
if img is None:
print('Failed to load fn:', fn)
sys.exit(1)
img = np.float32(img) / 255.0
cv2.imshow('input', img)
img = blur\_edge(img)
IMG = cv2.dft(img, flags=cv2.DFT\_COMPLEX\_OUTPUT)- Выводим на экран изображение и ползунки для изменения параметров: угол наклона функции распределения точки, диаметр PSF, SNR – отношение изображения к шуму.
Есть возможность исправить два вида изображений: размытие и смаз, размытие убирается, используя PSF в виде окружности, а смаз исправляется, используя PSF в виде линии. Переключать между этими функциями можно через клавишу Space. Первым ползунком мы регулируем угол наклона линии в PSF. Вторым ползунком изменяем диаметр фигуры в PSF. Третьим ползунком меняем SNR – величина отношения данных изображения к шуму.
cv2.namedWindow(win)
cv2.namedWindow('psf', 0)
cv2.createTrackbar('angle', win, 135, 180, update)
cv2.createTrackbar('d', win, 22, 50, update)
cv2.createTrackbar('SNR (db)', win, 25, 50, update)
update(None)- Обновляем картинку при изменении любых параметров.
def update(\_):
ang = np.deg2rad(cv2.getTrackbarPos('angle', win))
d = cv2.getTrackbarPos('d', win)
noise = 10 ** (-0.1 * cv2.getTrackbarPos('SNR (db)', win))
if defocus:
psf = defocus_kernel(d)
else:
psf = motion_kernel(ang, d)
cv2.imshow('psf', psf)
psf /= psf.sum()
psf_pad = np.zeros_like(img)
kh, kw = psf.shape
psf_pad[:kh, :kw] = psf
PSF = cv2.dft(psf_pad, flags=cv2.DFT_COMPLEX_OUTPUT, nonzeroRows=kh) # дискретное преобразование Фурье
PSF2 = (PSF ** 2).sum(-1)
iPSF = PSF / (PSF2 + noise)[..., np.newaxis]
RES = cv2.mulSpectrums(IMG, iPSF, 0)
# поэлементное умножение двух комплексных матриц, которые являются результатом действительного или комплексного преобразования Фурье. Ну или свертка.
res = cv2.idft(RES, flags=cv2.DFT_SCALE | cv2.DFT_REAL_OUTPUT)
# Вычисляет обратное дискретное преобразование Фурье для одномерного или двухмерного массива.
res = np.roll(res, -kh // 2, 0)
res = np.roll(res, -kw // 2, 1)
cv2.imshow(win, res)