Experimenting with different dynamical systems and simple control techniques.
Install the packages using the requirements.txt file.
# using conda
conda create --name control --file requirements.txt
# Or pip
pip install requirements.txtThe notebooks contain the implementations to: LQR and handpicking poles for the gain matrices to solve the pendulum and cartpole dynamical systems with linear control, Neural ordinary differential equations (ODEs).
The equations to the linear control techniques finding an appropriate Gain matrix K by handpicking the poles or using LQR on the Pendulum and Cartpole dynamical systems.
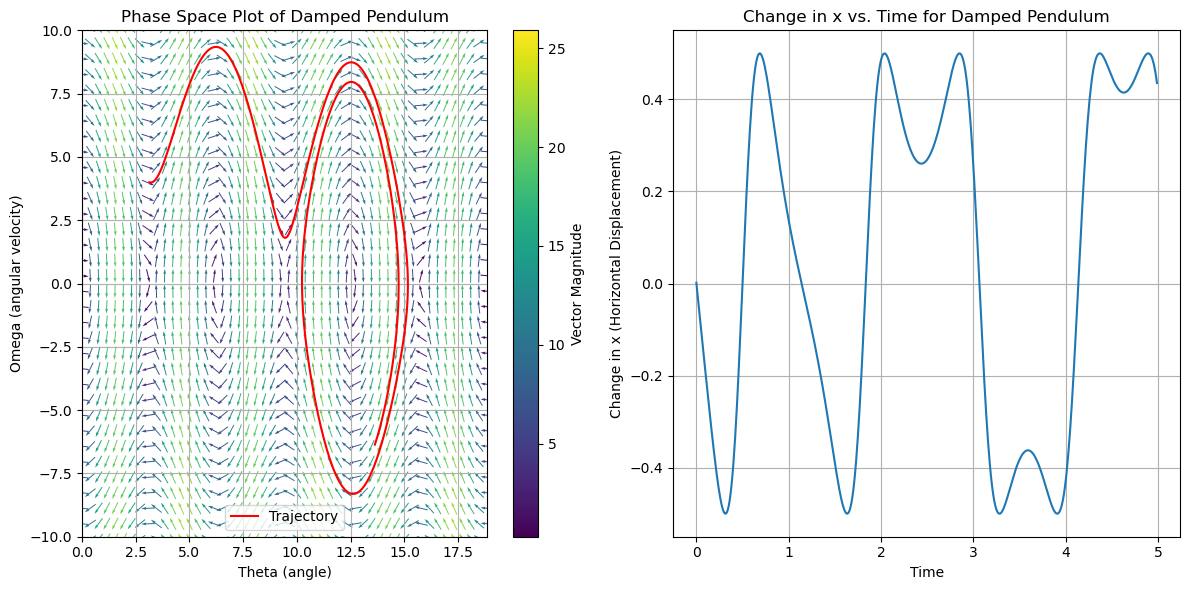
An example of the Pendulum phase space and a specific trajectory:
Visualization of the neural ODE trajectory.
- Steven L. Brunton, Joshua L. Proctor, & J. Nathan Kutz (2016). Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings of the National Academy of Sciences, 113(15), 3932–3937.
- Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, & David Duvenaud. (2019). Neural Ordinary Differential Equations.
Many thanks to the amazing course on "Differential Equations & Dynamical Systems" by Steve Brunton, and author of this github repository for sharing his version of cartpole for simple experimentation, https://github.com/billtubbs/gym-CartPole-bt-v0/ and on neural ODEs notebooks, https://uvadlc-notebooks.readthedocs.io/en/latest/index.html.