NIRVANA: Uncertainty-Aware Prediction Validator in Deep Learning Models for Cyber-Physical System Data
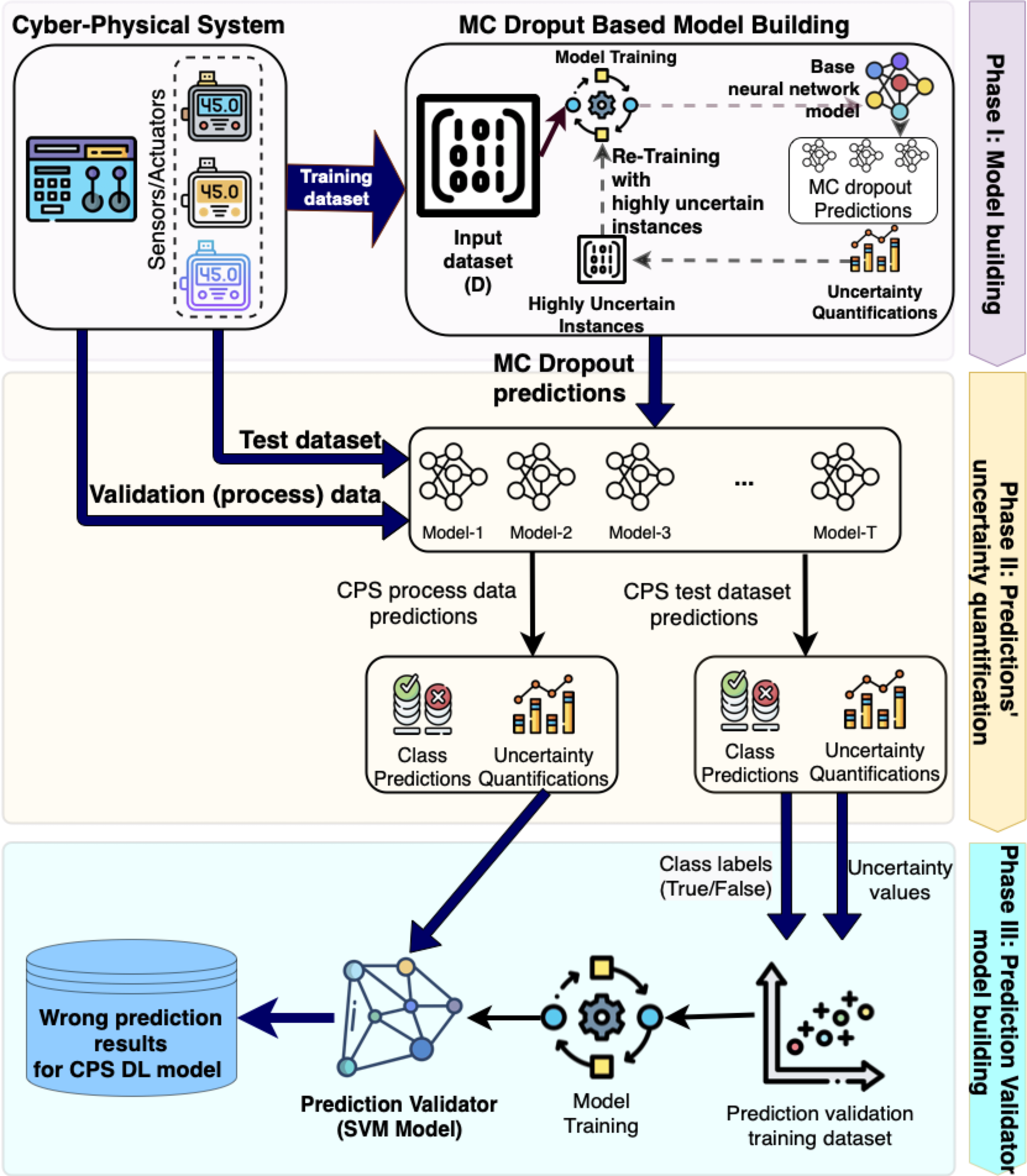
The use of Deep learning in Cyber-Physical Systems (CPSs) is gaining popularity due to its ability to bring intelligence to CPS behaviors. However, both CPSs and deep learning have inherent uncertainty. Such uncertainty, if not handled adequately, can lead to unsafe CPS behavior. The first step towards addressing such uncertainty in deep learning is to quantify uncertainty. Hence, we propose a novel method called NIRVANA (uNcertaInty pRediction ValidAtor iN Ai) for prediction validation based on uncertainty metrics. To this end, we first employ prediction-time Dropout-based Bayesian Neural Networks to quantify uncertainty in deep learning models applied to CPS data, and used two uncertainty metrics, i.e., entropy and variance-based metrics. Second, such quantified uncertainty is taken as the input to predict wrong labels using a support vector machine with radial basis function kernel, with the aim of building a highly discriminating prediction validator model with uncertainty values. In addition, we investigated the relationship between uncertainty quantification and prediction performance, and conducted experiments to obtain optimal dropout ratios. We conducted all the experiments with four real-world CPS datasets. Results show that uncertainty quantification is negatively correlated to prediction performance of a deep learning model of CPS data. Also, our dropout ratio adjustment approach is effective in reducing uncertainty of correct predictions while increasing uncertainty of wrong predictions.
- F. Ozgur Catak https://www.uis.no/nb/profile/ferhat-ozgur-catak-0
- Tao Yue https://www.simula.no/people/tao
- Shaukat Ali https://www.simula.no/people/shaukat
- Catak, F. O., Yue, T., & Ali, S. (2022). Uncertainty-Aware Prediction Validator in Deep Learning Models for Cyber-Physical System Data. ACM Transactions on Software Engineering and Methodology (TOSEM), 31(4), 1-31.