Model Predictive Control with discrete-time Control Barrier Functions (MPC-CBF) for a wheeled mobile robot.
The MPC-CBF optimization problem is given by:
$$\begin{aligned}
\min_{u_{t: t+N-1 \mid t}} \quad & \frac{1}{2} \tilde{x}_N^T Q_x \tilde{x}_N+\sum_{k=0}^{N-1} \frac{1}{2} \tilde{x}_k^T Q_x \tilde{x}_k+\frac{1}{2} u_k^T Q_u u_k\\\
\textrm{s.t.} \quad
& x_{t+k+1 \mid t}=x_{t+k \mid t}+f\left(x_{t+k \mid t}, u_{t+k \mid t}\right) \cdot T_s, \quad k=0, . ., N-1,\\\
& x_{\min } \leq x_{t+k \mid t} \leq x_{\max }, \quad k=0, \ldots, N-1,\\\
& u_{\min } \leq u_{t+k \mid t} \leq u_{\max }, \quad k=0, \ldots, N-1, \\\
& x_{t \mid t}=x_t, \\\
& \Delta h\left(x_{t+k \mid t}, u_{t+k \mid t}\right) \geq-\gamma h\left(x_{t+k \mid t}\right), \quad k=0, \ldots, N-1 \\\
\end{aligned}$$
where $\tilde{x}_k=x_{des,k} - x_{k}$.
Path comparison for different values of γ for MPC-CBF and with MPC-DC
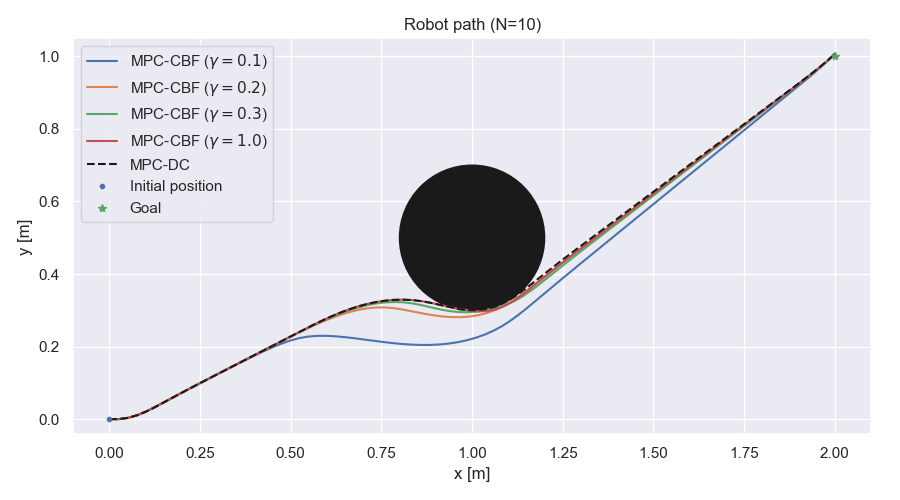
Path comparison
MPC-CBF
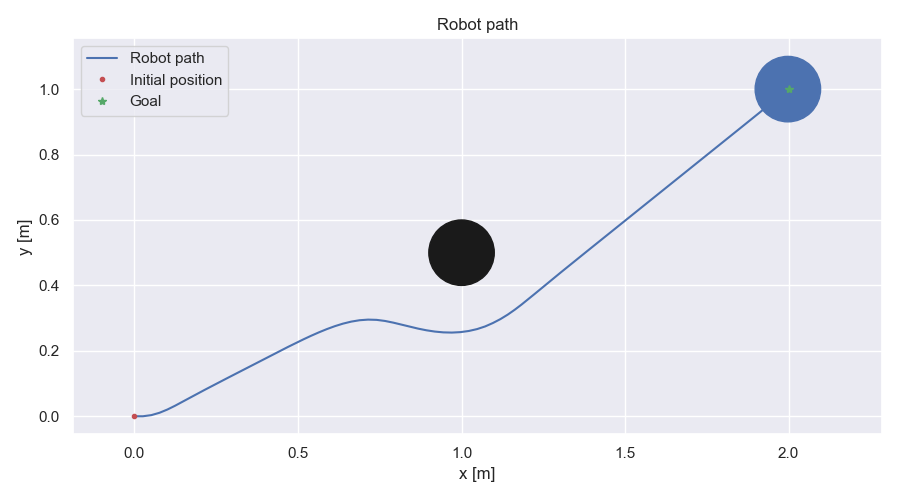
Robot path
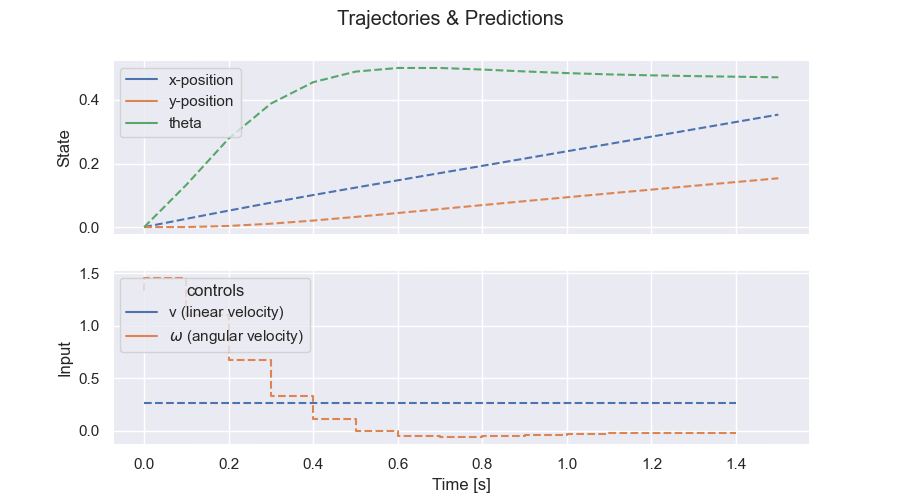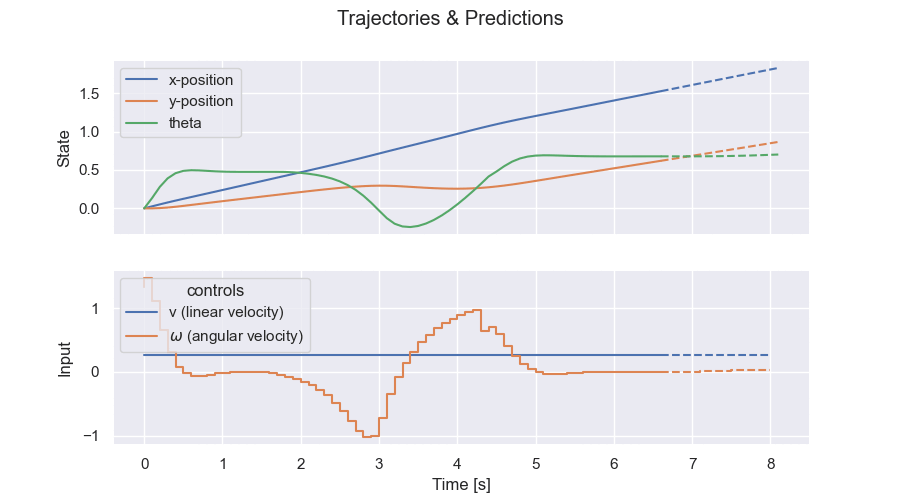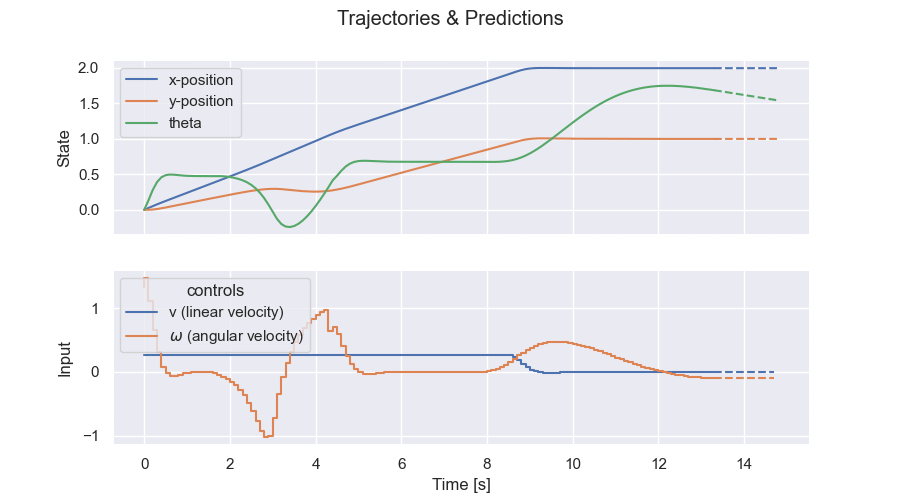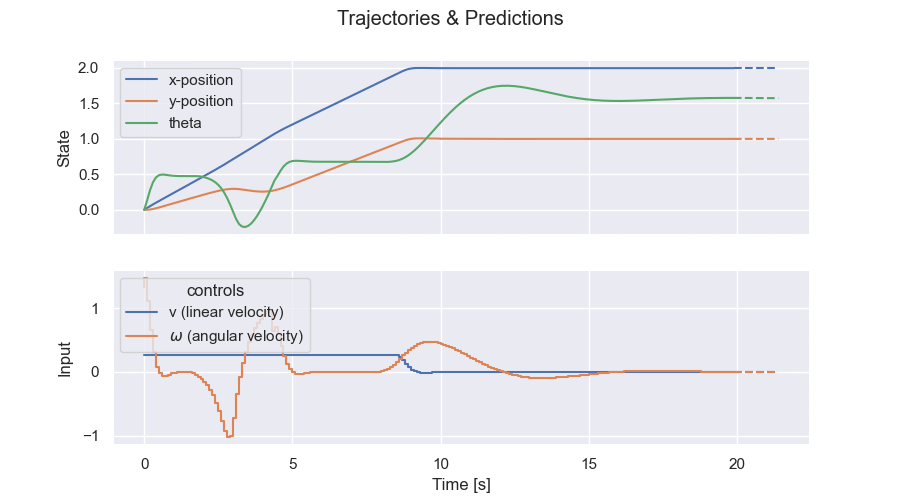
Trajectories
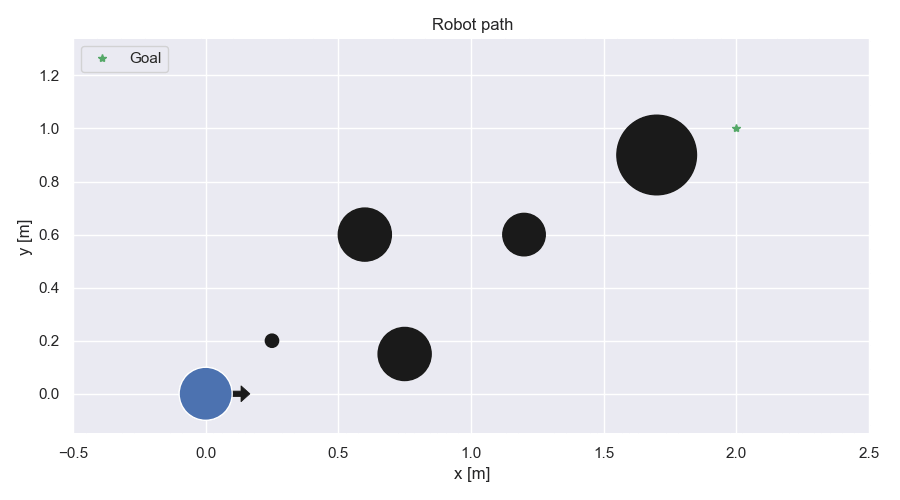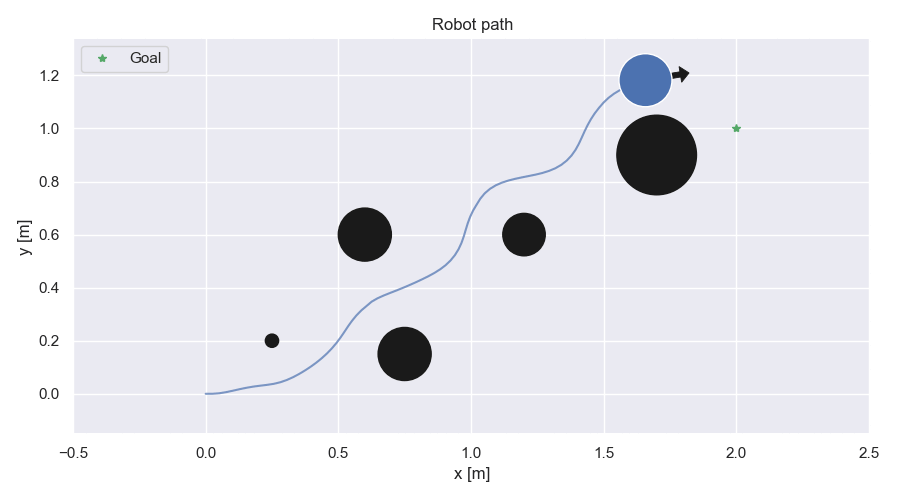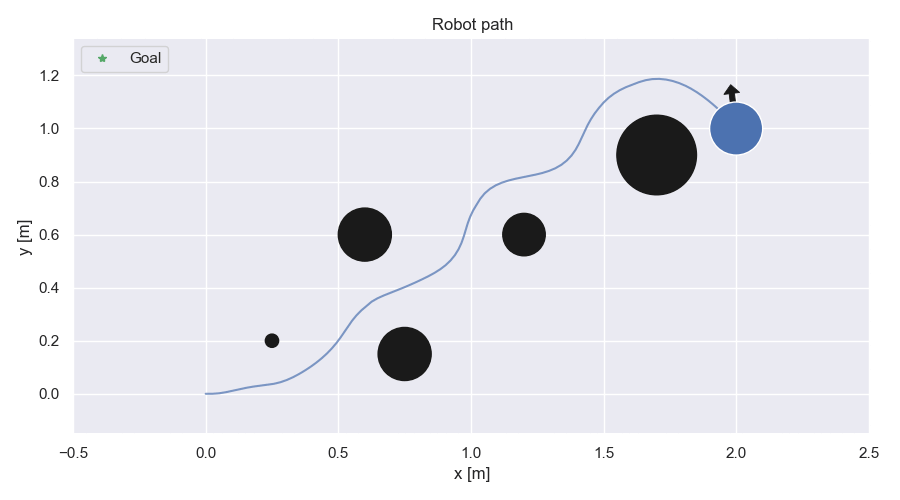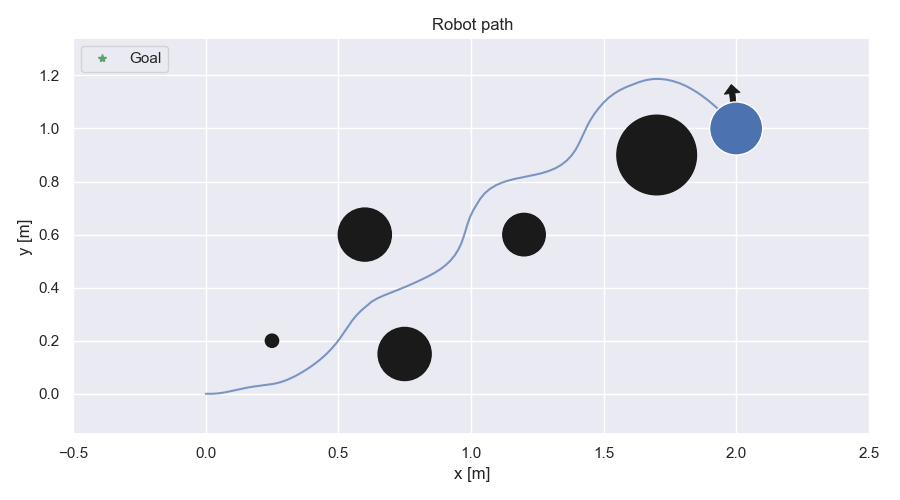
Robot path
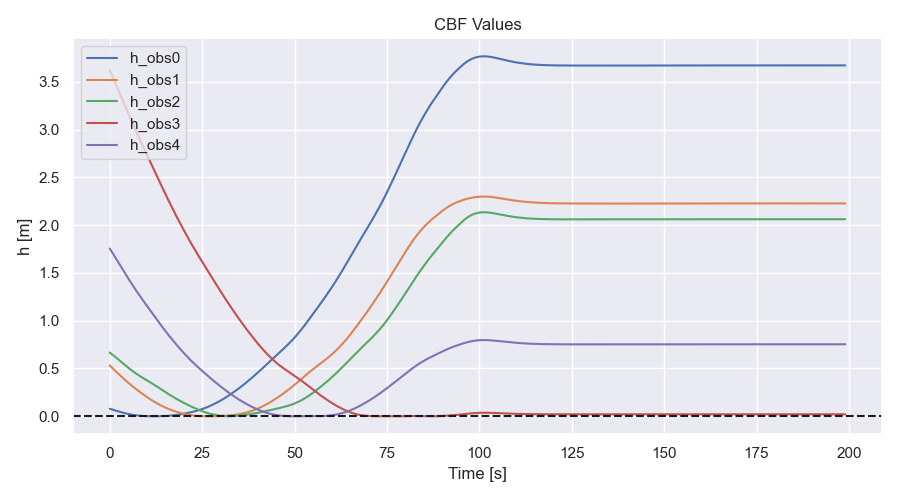
CBF values
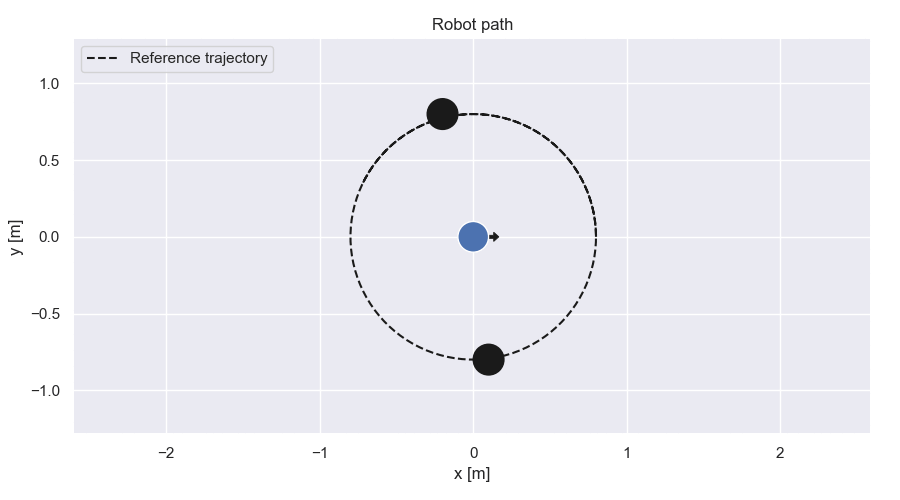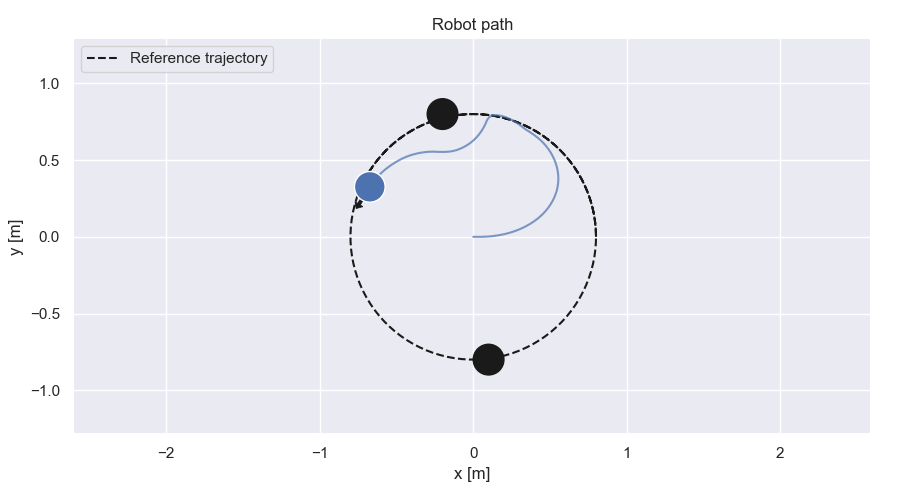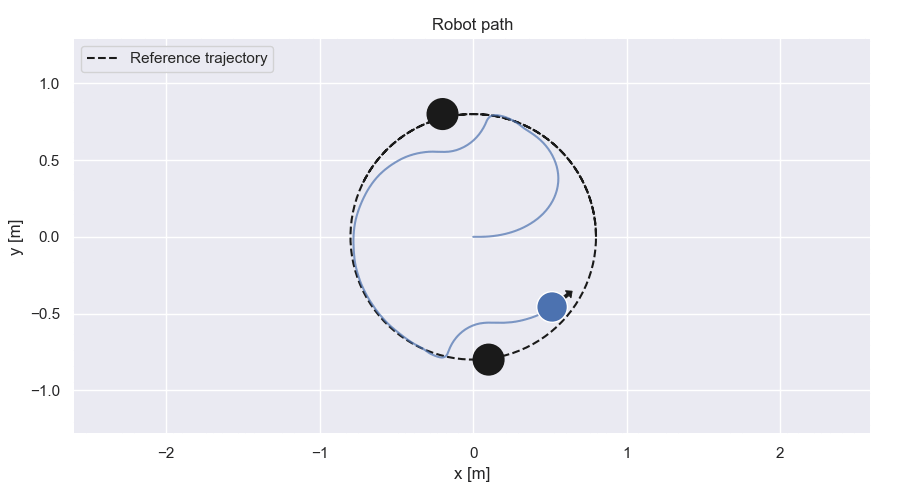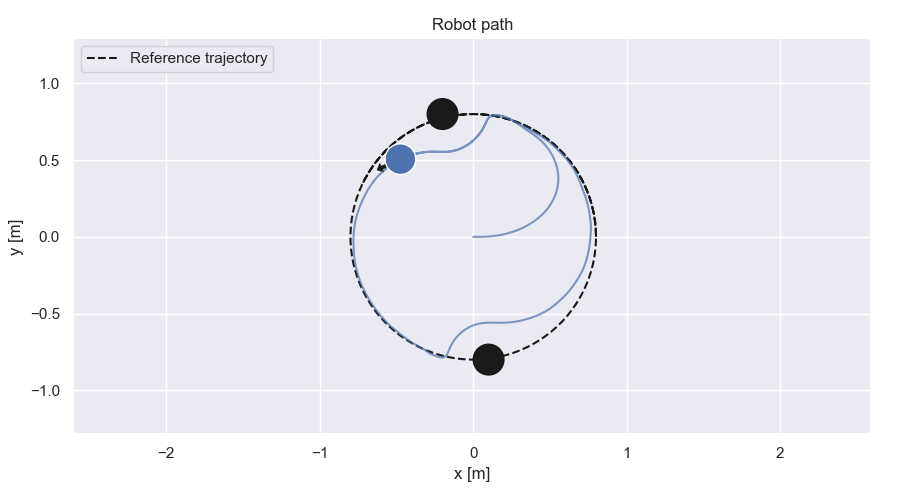
Robot path
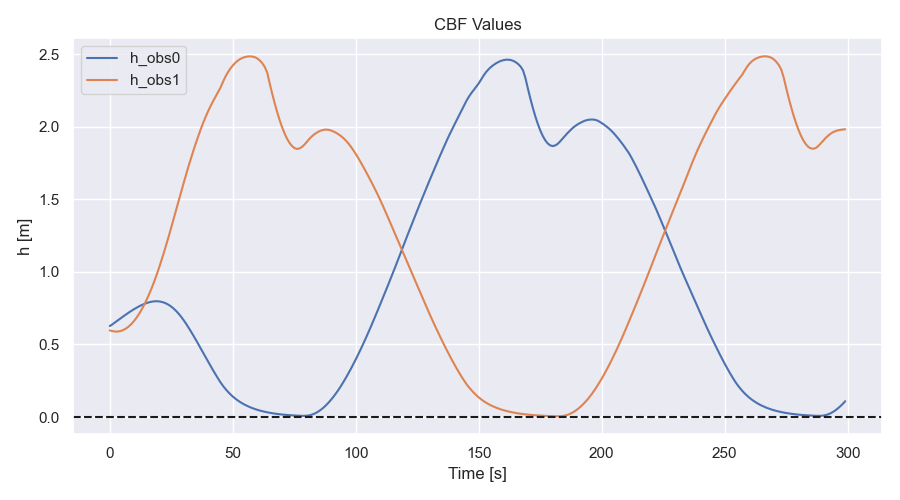
CBF values

Trajectories
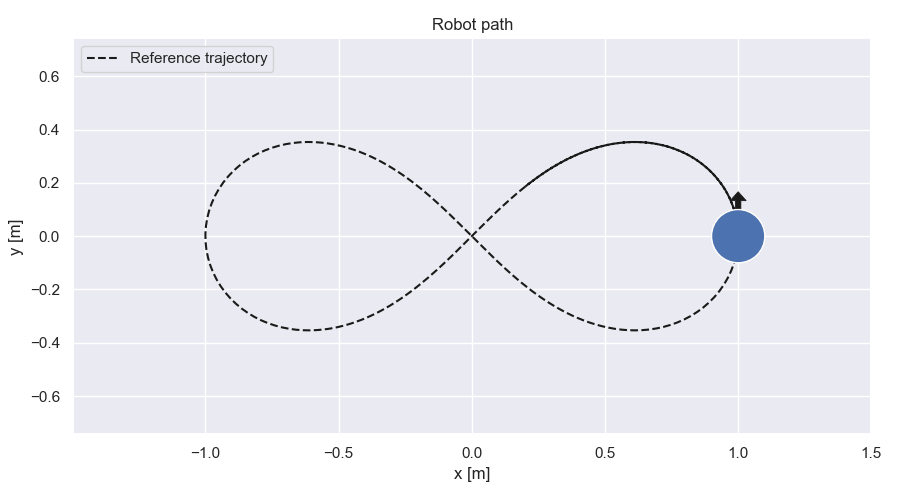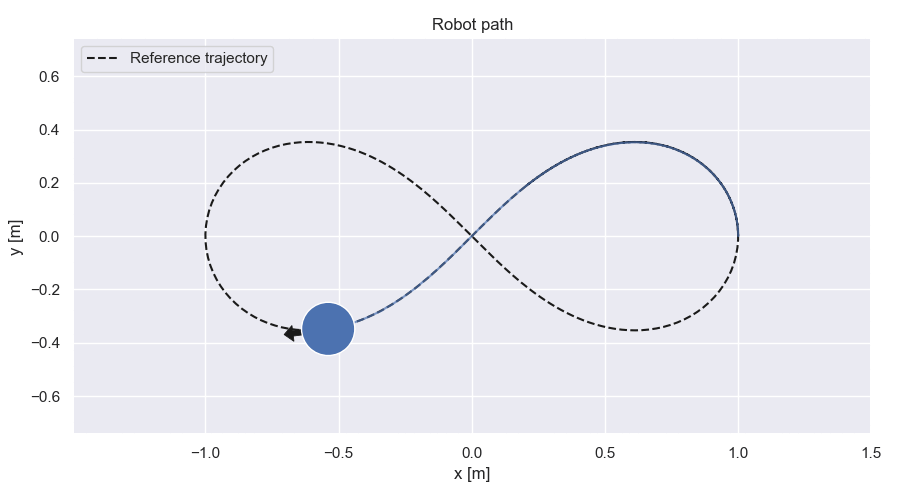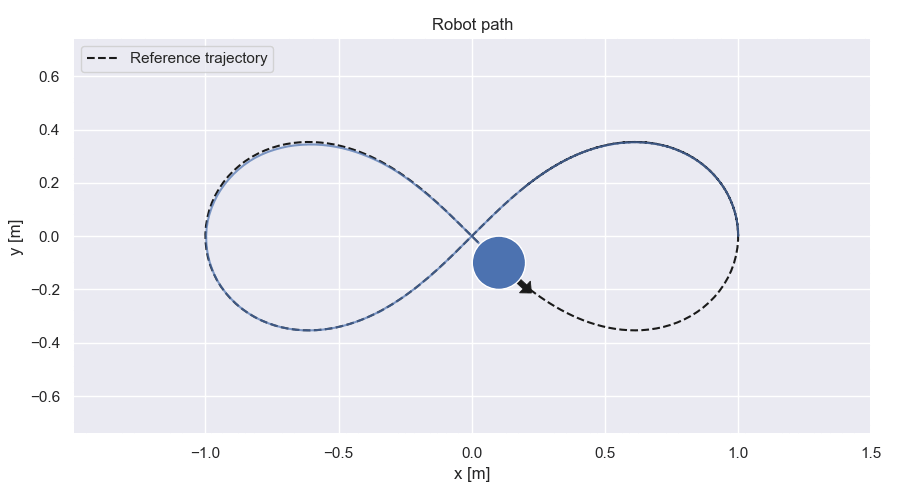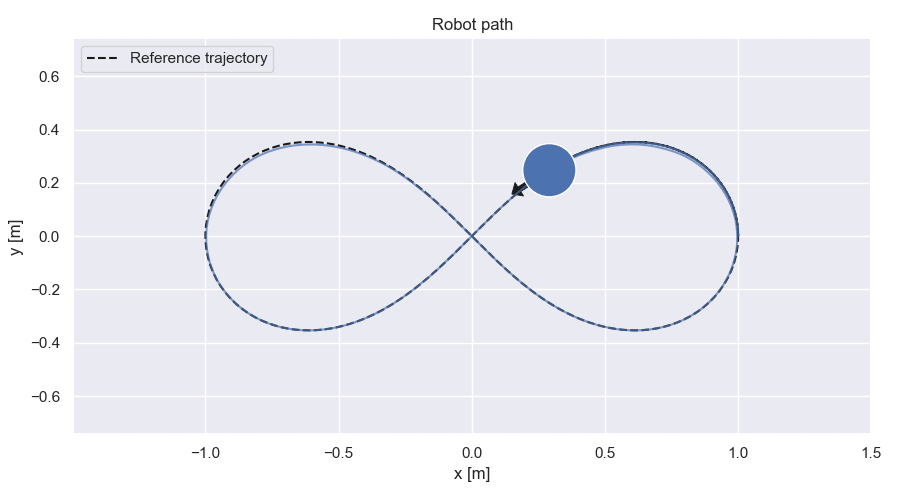
Robot path
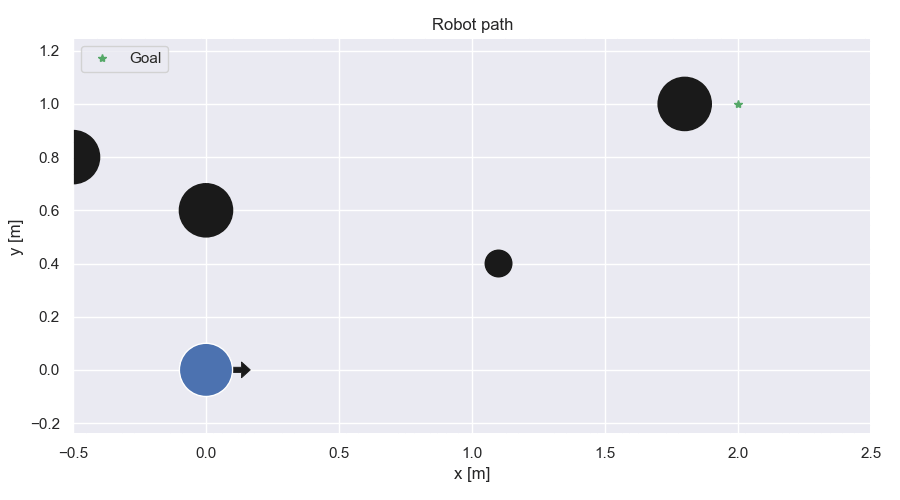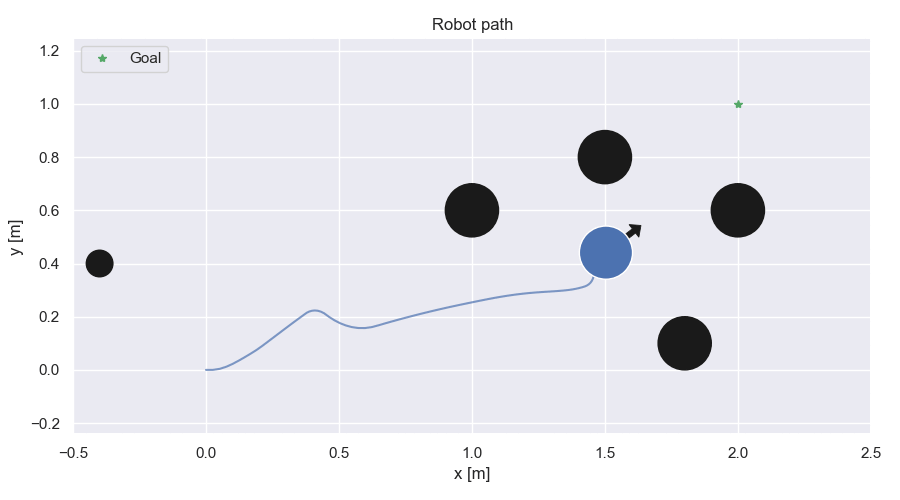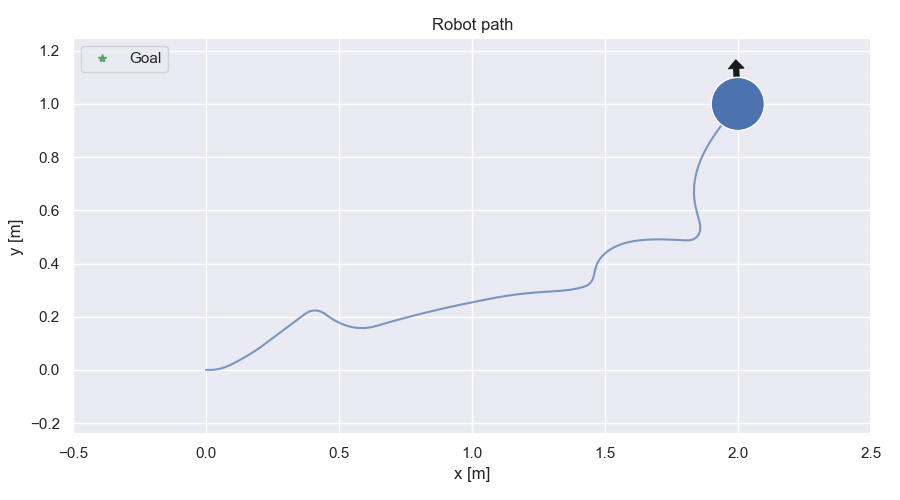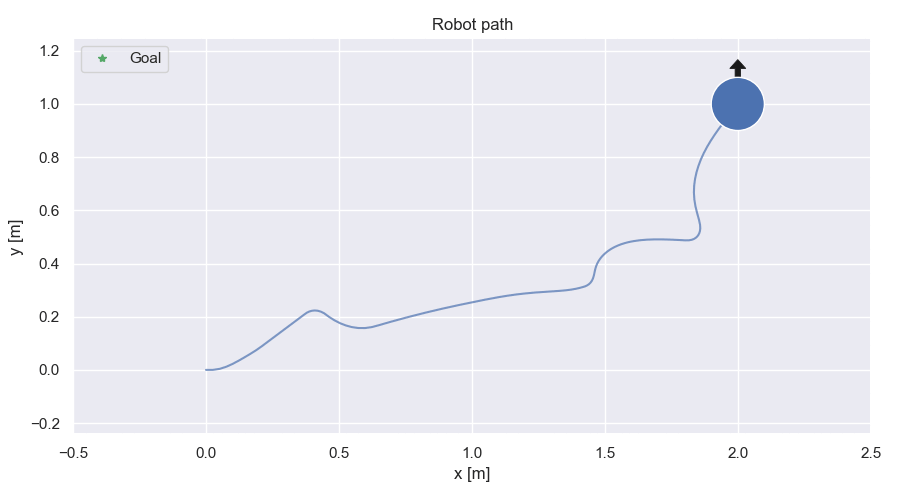
Robot path
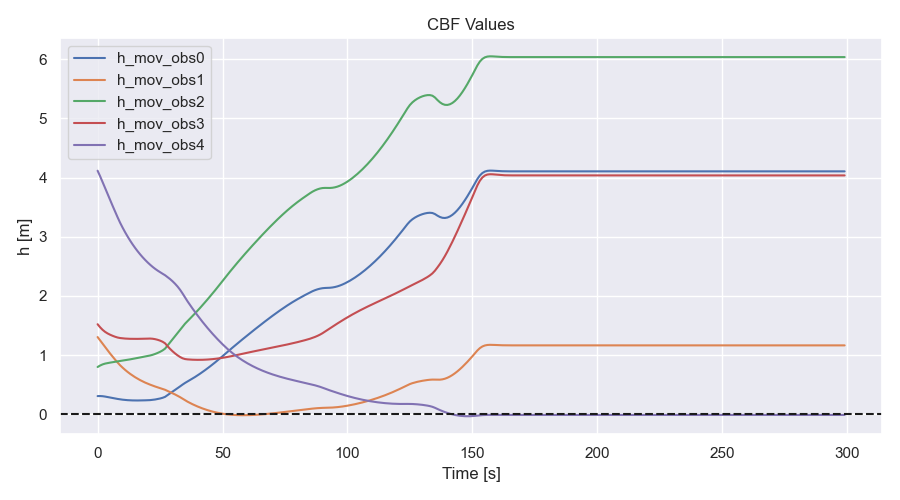
CBF values
Gazebo simulation with turtlebot3
To use this project, install it locally via:
git clone https://github.com/elena-ecn/mpc-cbf.git
The dependencies can be installed by running:
pip install -r requirements.txt
The controller configuration can be changed through the config.py.
To execute the code, run:
The contents of this repository are covered under the MIT License.












