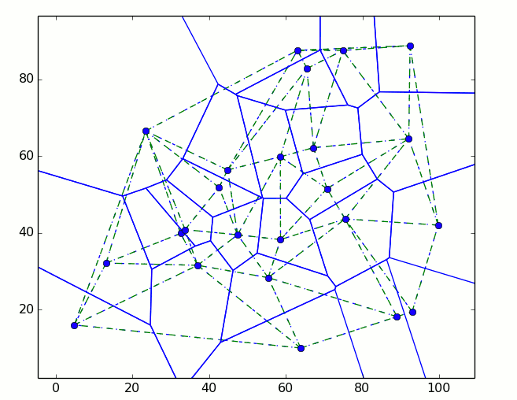
A Simple Delaunay triangulation and Voronoi diagram constructor in 2D. Written by Jose M. Espadero
Just pretend to be a simple and didactic implementation of the Bowyer-Watson algorithm to compute the Delaunay triangulation and the Voronoi diagram of a set o 2D points.
It is written in pure python + numpy (tested with python2.7 and python3). A test example is provided showing how to call and plot the results using matplotlib.
It support the robust inCircle2D predicate from Jonathan Richard Shewchuk, but it is disabled by default due to perfomance penalties, so do not expect to work on degenerate set of points. If you really need to compute triangulation on big or degenerate set of points, try scipy.spatial.Delaunay instead.
Here is a minimal example of building a triangulation and dump the result to console.
import numpy as np
from delaunay2D import Delaunay2D
# Create a random set of points
seeds = np.random.random((10, 2))
# Create Delaunay Triangulation and insert points one by one
dt = Delaunay2D()
for s in seeds:
dt.addPoint(s)
# Dump points and triangles to console
print("Input points:\n", seeds)
print ("Delaunay triangles:\n", dt.exportTriangles())No. This code has been written to stay simple, easy to read by beginners and with minimal
dependencies instead of highly-optimized. There is a section in addPoint() method that
performs specially bad if you have a big set of input points:
# Search the triangle(s) whose circumcircle contains p
for T in self.triangles:
if self.inCircle(T, p):
bad_triangles.append(T)Here, we should avoid iterating over the complete list of triangles. Best way is to use a structure that allows a spatial search (as a QuadTree). Then, continue the search over the neighbours of the initial search.
Despite that, it will compute DT of less than 1000 points in a reasonable time. If you really need to compute triangulation on huge or degenerate sets of points, try scipy.spatial.Delaunay, which is based on Qhull library
Mainly, to provide a didactic implementation of the algorithm. Also, because sometimes it is not possible/worth to import the complete scipy.spatial package (for example, when running a script inside of python interpreter included in blender )