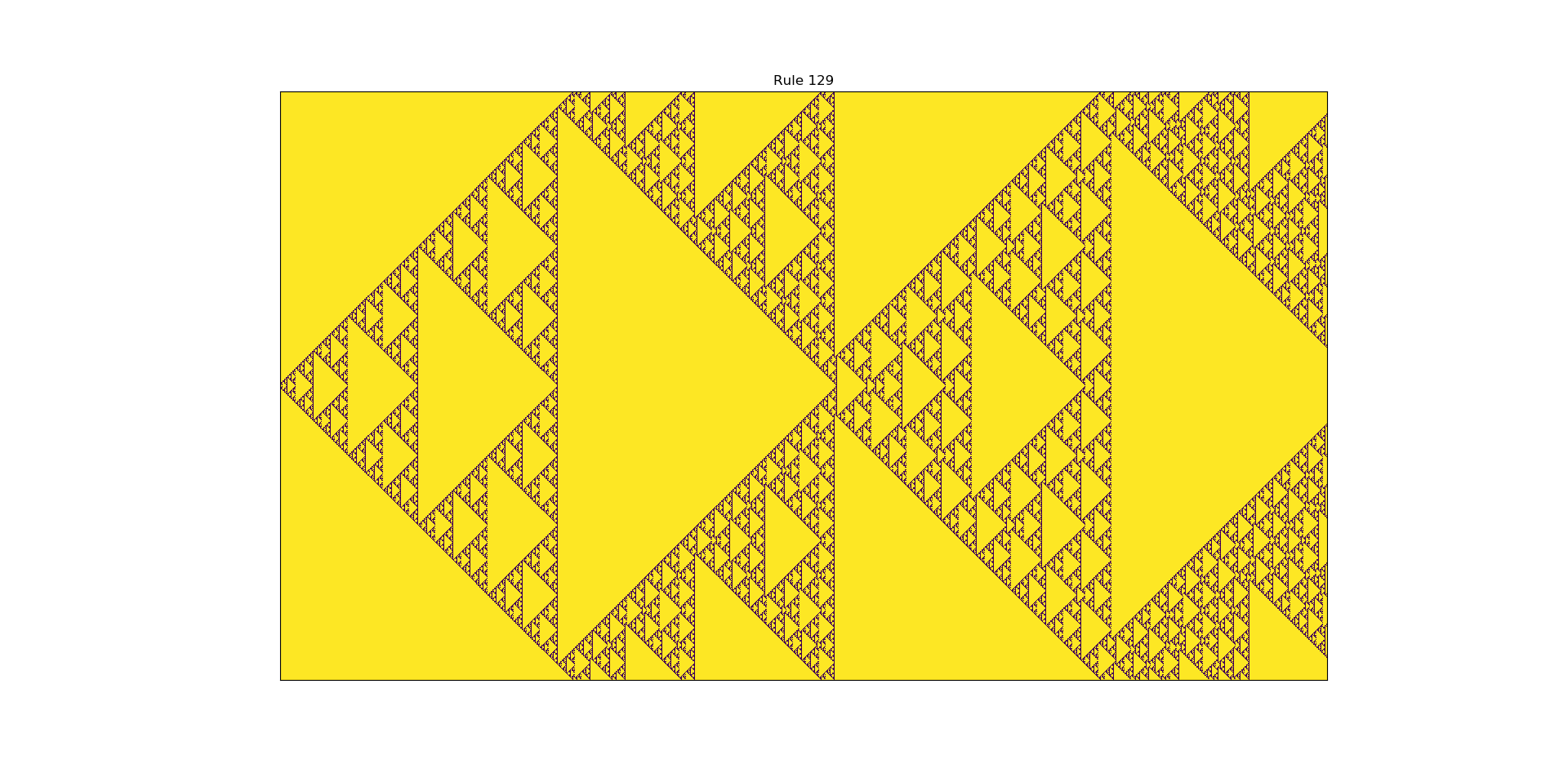
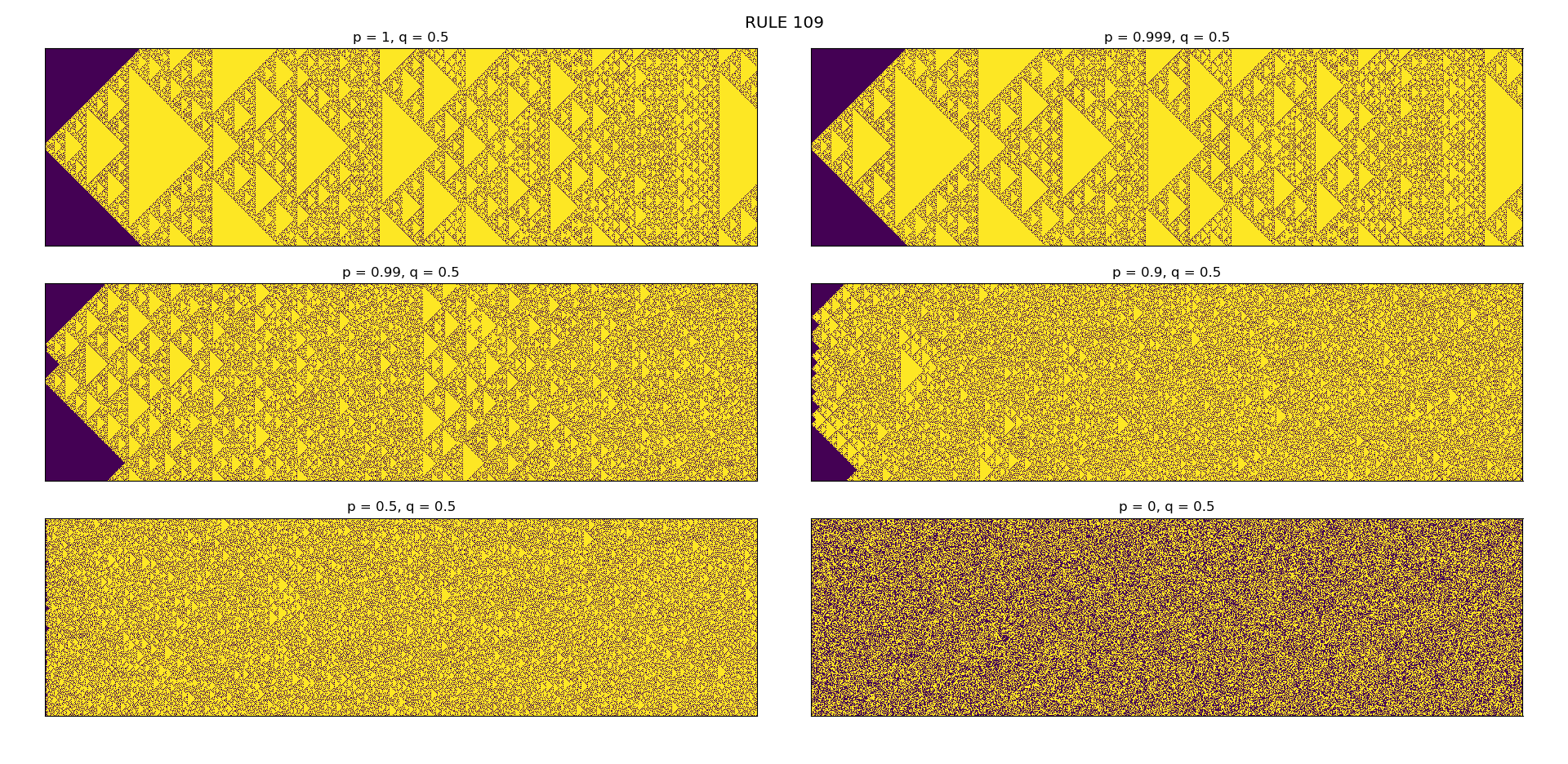
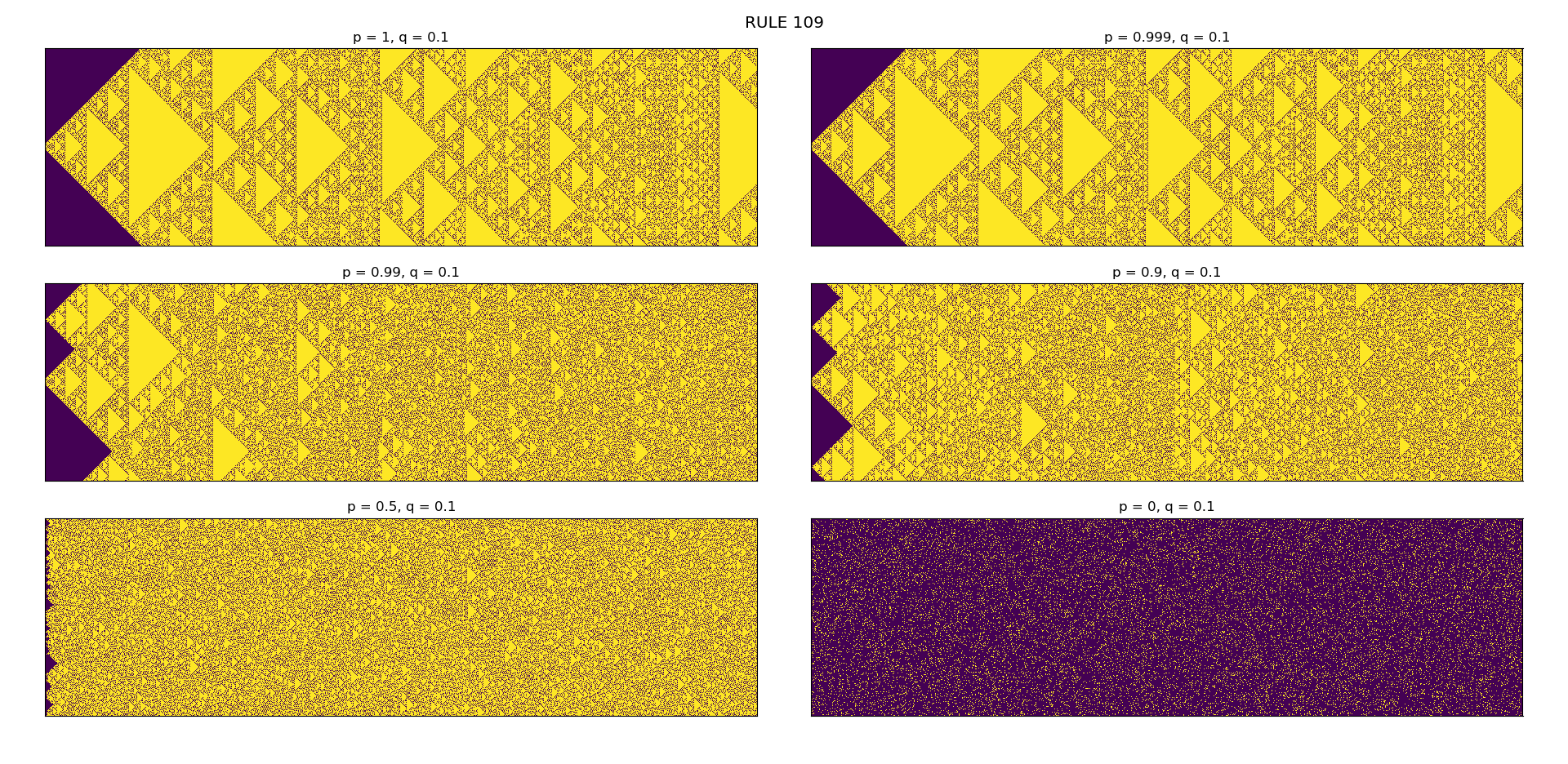
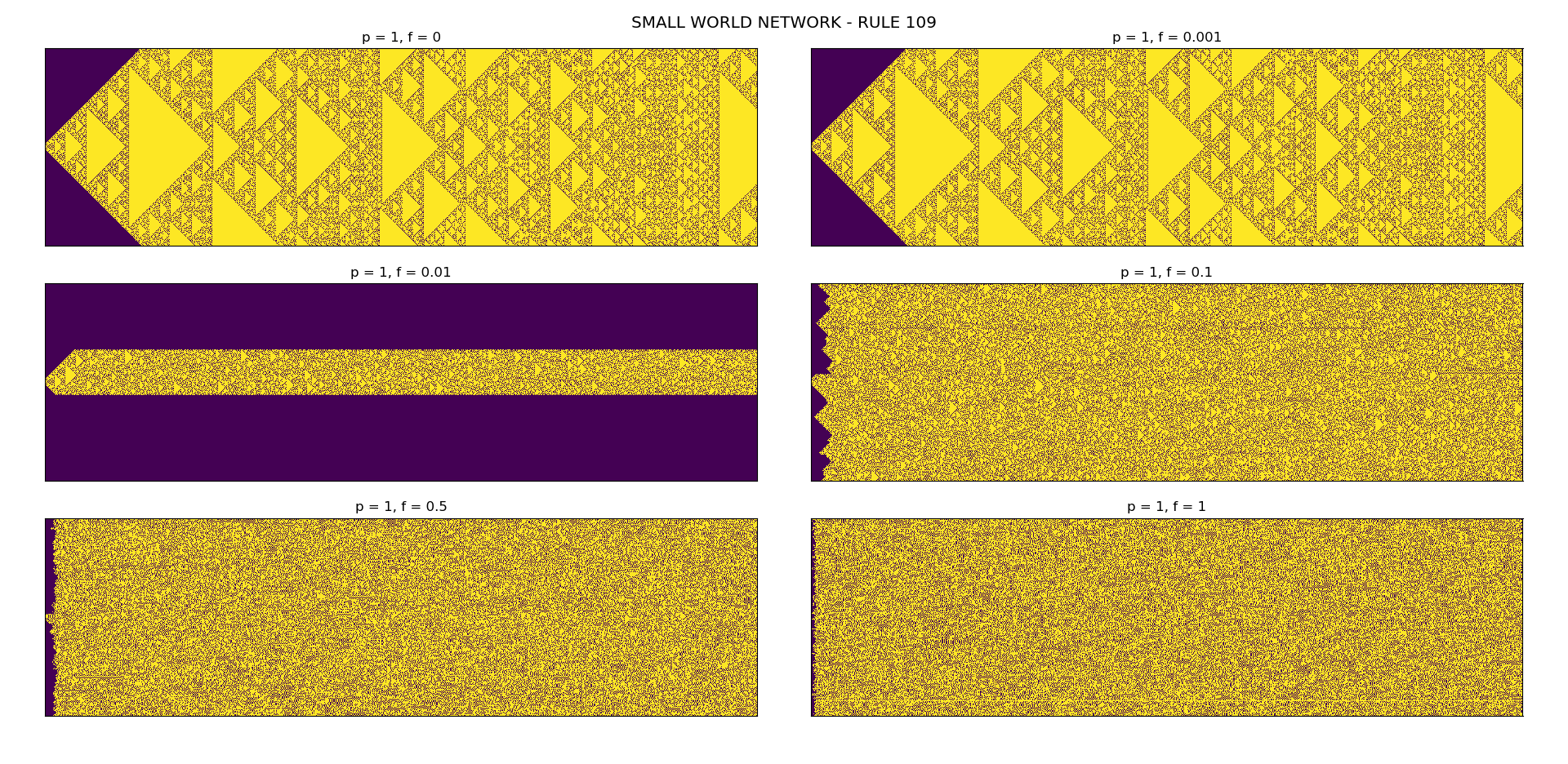
1D Cellular Automata (CA) for any rule in the range of 0 to 255 can be drawn using this code.
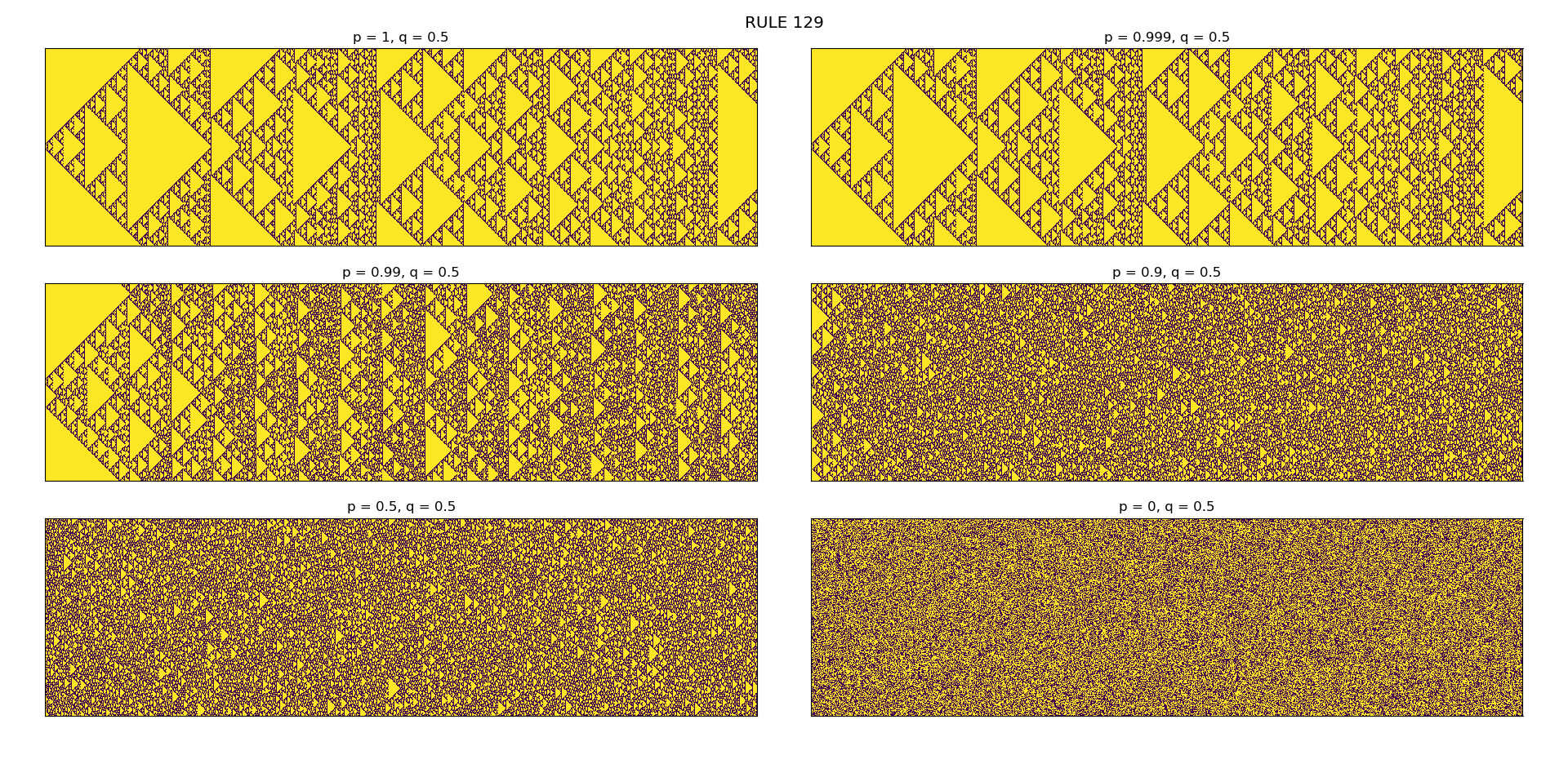
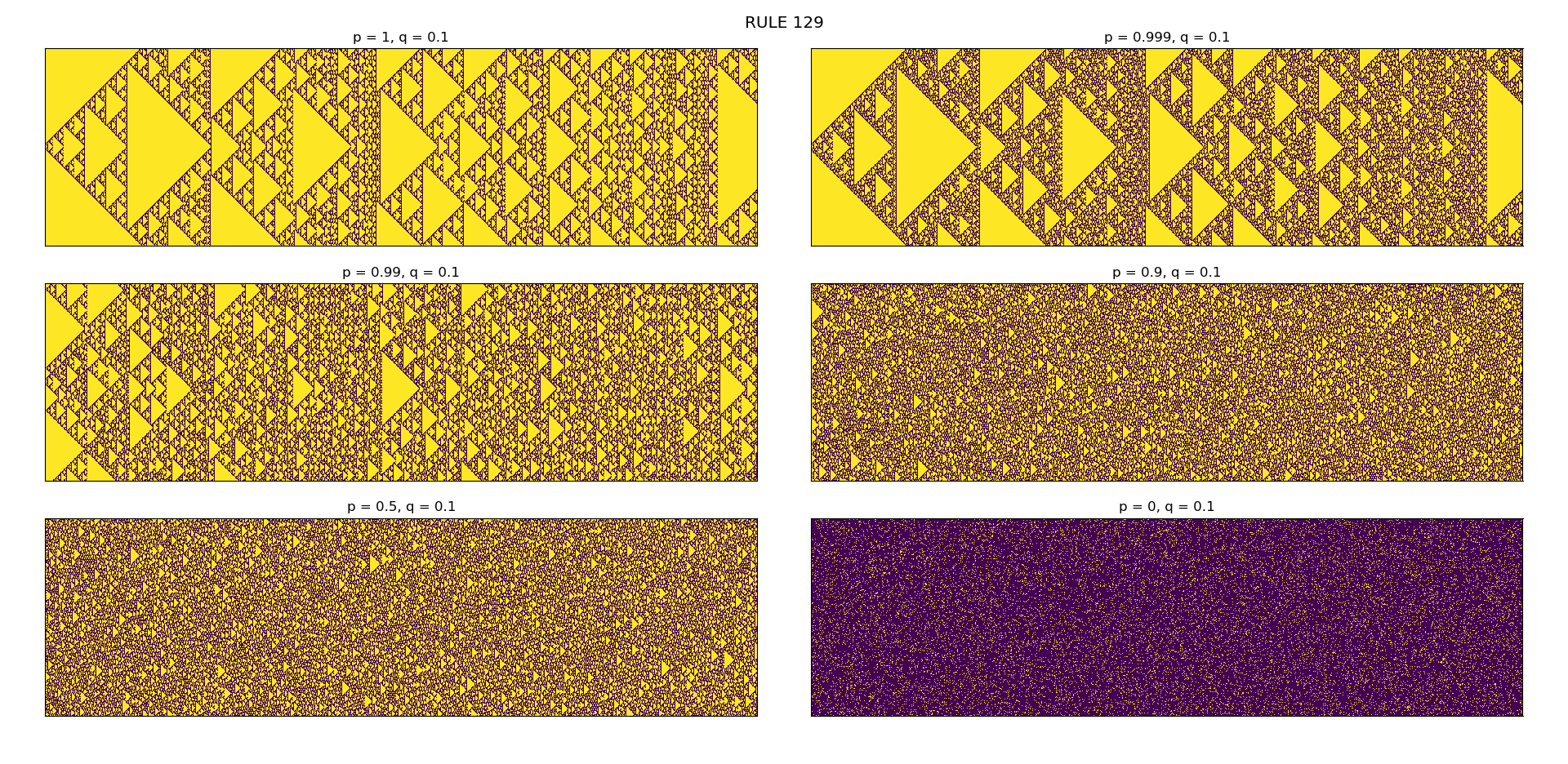
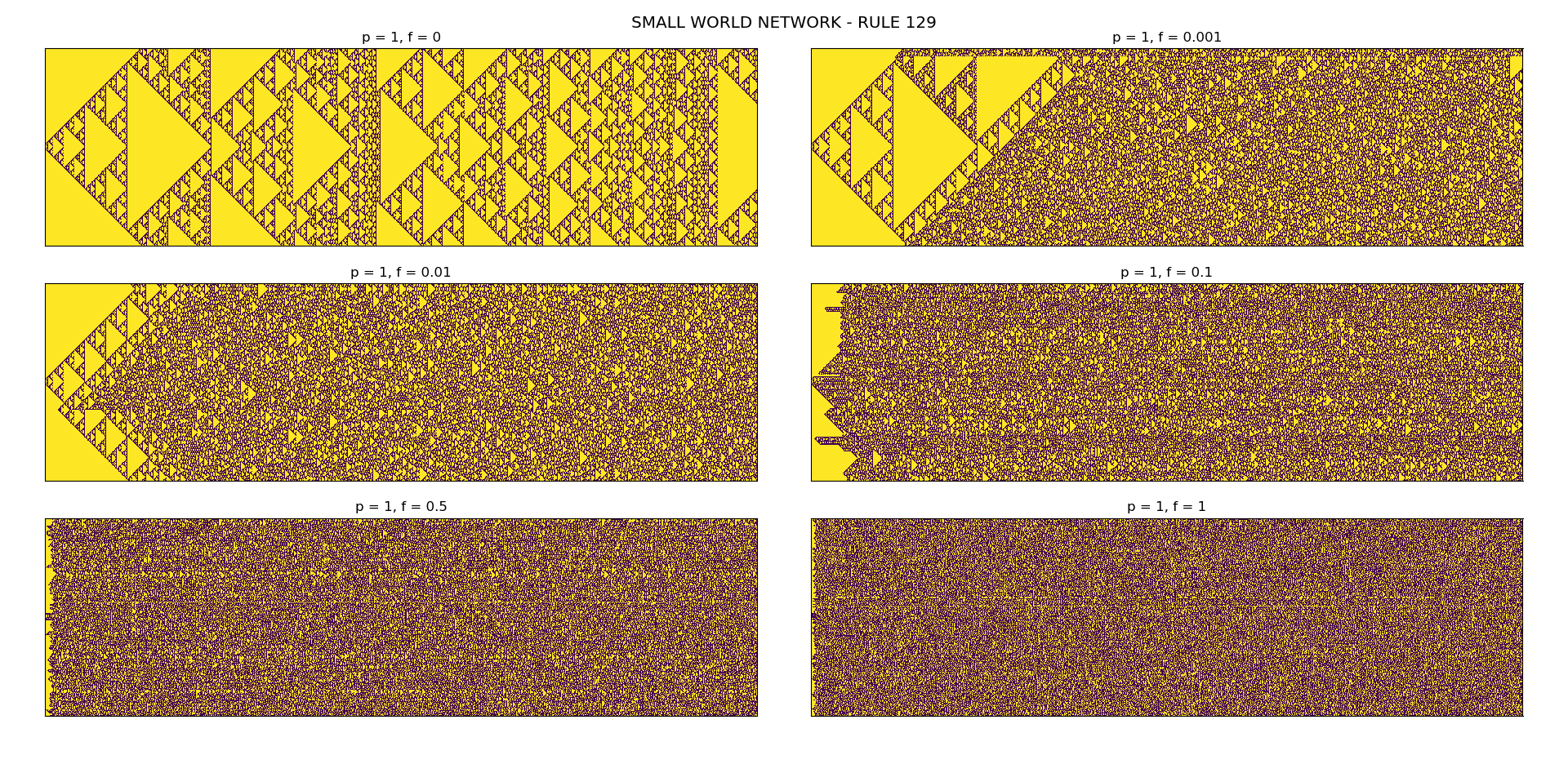
p- probability of CA-world to follow given CA ruleq- probability of choosing on or off state of the cell randomly whenp>0f- fraction of cells in CA-world which will choose neighbors randomlyconfig- random or uniform
Along with well known 1d cellular automata rules, there are implementations of few interesting variations described below
One can analyze the effect of noise in the CA-world. It is interesting to observe how a simple rule starting in a uniform CA-world can also result in a chaotic behavior with beautiful patterns.
I have shown Rule 129 and Rule 161 as an example. Both the rules show same fractal pattern of Sierpinski triangle but both result in completely different result when noise is inserted.
For this to be implemented, a small change in neighborhood of CA-cell in each rule is made. The fraction f of cells are selected randomly and neighbors are assigned randomly to these selected cells. Based on neighborhood changes, if one uses a deterministic CA rule (without any noise p=0), the results show variation of patterns. Even with small value of f, huge changes can be observed.