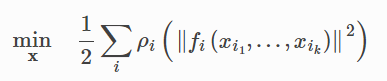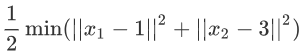NOPY is an extension of scipy.optimize.least_squares. It provides a much more flexible and easier-to-use interface than the original scipy.optimize.least_squares. You will love it if you are familiar with Ceres Solver.
NOPY can solve robustified non-linear least squares problems with bounds of the form
The expression 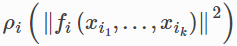 is known as a residual block, where
is known as a residual block, where 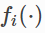 is a residual function that depends on one or more variables
is a residual function that depends on one or more variables  .
.
git clone https://github.com/aipiano/NOPY.git
cd NOPY
pip install .
We wanna minimize the following naive cost function
The first step is to define residual functions.
def f1(x1):
return x1 - 1
def f2(x2):
return x2 - 3Then we define variables with some initial values.
x1 = numpy.array([-1], dtype=numpy.float64)
x2 = numpy.array([0], dtype=numpy.float64)Next, we build the least squares problem and use the '2-point' finite difference method to estimate Jacobian matrix of each residual block.
problem = nopy.LeastSquaresProblem()
problem.add_residual_block(1, f1, x1, jac_func='2-point')
problem.add_residual_block(1, f2, x2, jac_func='2-point')The first argument of add_residual_block is the dimension of residual function. In this example, the residual function return a scalar, so the dimension is 1.
Finally, we solve it.
problem.solve()Now all variables should have the right value that make the cost function minimum.
print(x1) # x1 = 1
print(x2) # x2 = 3If you don't want to change one or more variables during optimization, just call
problem.fix_variables(x1)and unfix them with
problem.unfix_variables(x1)For variable bounding, just call
problem.bound_variable(x1, 0, 1)and unbound it with
problem.bound_variable(x1, -np.inf, np.inf)Note that the initial value of a bounded variable must lie in the boundary.
NOPY support robust loss functions. You can specify loss function for each residual block, like bellow
problem.add_residual_block(1, f1, x1, jac_func='2-point', loss='huber')Custom jacobian function and loss function are also supported just like scipy.optimize.least_squares. You can find more examples in the 'examples' folder.