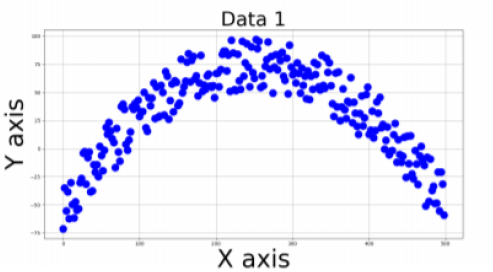
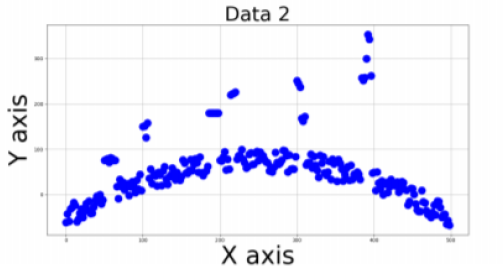
Two files of 2D data points are provided in the form of CSV files. The data represents measurements of a projectile with different noise levels. Data sets are shown below:
The solution finds a best fit curve to these data sets using RANSAC and least squares algorithm.
-
We can use the Least-Square method to fit a curve to the data-model as the data-points are close to each other giving a quadratic shape to the distribution of x v/s y data.
-
As the values of x-column are evenly spaced we can go with Least-Square method only (if there could have been some irregular distribution in the values of x, we could have chosen Total-Least-Square as the basic model to fit the curve, but not in this case)
-
Using least-square method to find the solution of P in the the equation AP = Y we get:
P = (ATA)-1(ATY)
- We can observe that few points (can be termed as outliers) in the this data set are far away from most of the points that are roughly following specific pattern/trend (quadratic curve)
- If we try to fit a curve using just least-square method, the curve might be shifted towards the outliers too in order to reduce the distance between them and will not be able to describe the data better.
- We can use RANSAC (RANdom SAmple Consensus) algorithm to fit a better curve that can describe the data-set better and also help in detecting/identifying the outliers too.
- In RANASC, as the same suggests, we will sample few of the data points in our dataset and try fitting a curve to the sampled data.
- We count the number of points whose distance from the line lie within a specific predefined threshold.
- Iterate again with new sample points, solve for the model, count the inliers and check whether the inlier count is greater than any of the previous ones.
- We select the model which has the maximum number of inliers and that will be our solution to P.
- To select the model for the sampled data set we used Least-Square model method similar to the way it was done for dataset-1.
- Few of the parameters that were chosen for our solution:
- N = number of iterations : this was adaptively updated based on number inliers for each model
- N = log(1 - p) / log(1 - (1 - e)num_samples), where p = desired probability of the inliers, e = probability of the outliers, num_samples = number of samples of data we chose for each iteration.
- number of sample = 3, minimum three equations are required to get the values of three parameters: a, b and c in ax2 + bx + c
- p = 0.95, so that most of the points can be covered or described by the model
- e = 1 - inlier_count/total_data_size (it is adaptive)
- threshold = standard deviation of y/2, having a narrow boundary and checking maximum inliers in it increases the desired overall probability of the inliers.
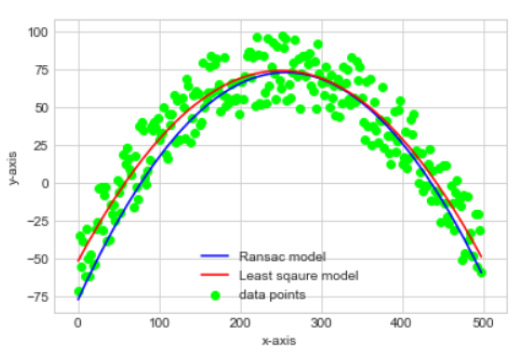
Representation of curves for dataset 1:
We can see that the model estimated by least-square(LS) method (in red) and the one estimated by RANSAC method (blue) lie very close to each other. This suggests that LS method anyway shows good results with data that does not have abnormal points/noise/outliers.
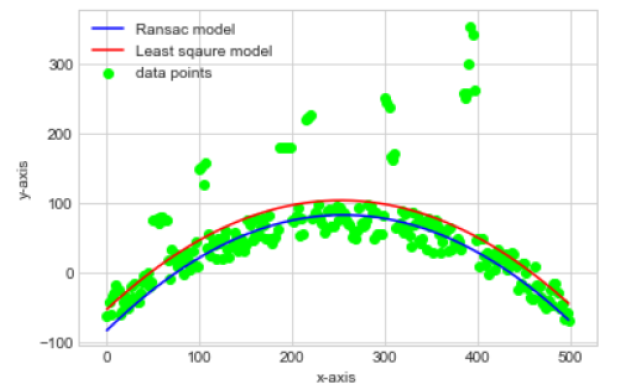
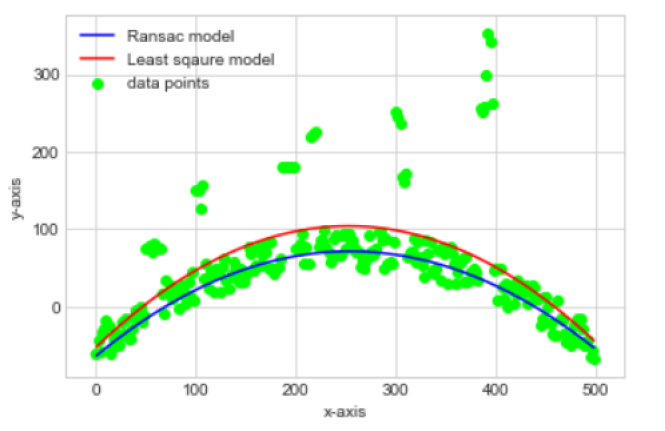
Representation of curves for dataset 2 when, threshold = standard deviation/2:
The curve estimated by LS method (red) can be seen moving towards the outlier points too, whereas the the curve estimated by RANSAC method (blue) lies somewhere at the center of the data-points that together define a quadratic trend more genuinely.
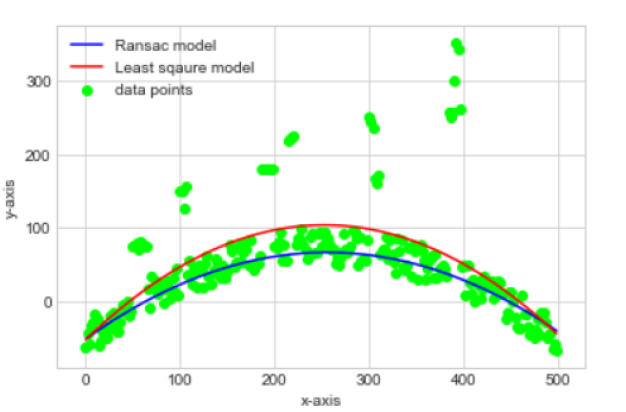
Representation of curves for dataset 2 when, threshold = standard deviation/3:
Representation of curves for dataset 2 when, threshold = standard deviation/5:
python file named ‘modelfitting.py’ (location: /<directory_id>/Code/) is to be run for the execution of the code:
Please make sure the following files are at the same directory location/level:
- modelfitting.py
- ransac.py
- linearleastsquare.py
- data_1.csv
- data_2.csv
Steps to run: Go the terminal where one can run python scripts (python 3.x):
- in the terminal type and run: $ python modelfitting.py