EXPLORING TIME DISTANCE TRADEOFFS IN MULTI-ROBOT TASK ALLOCATION USING MULTIOBJECTIVE GENETIC ALGORITHMS
Final year project that explored solutions to multi objective multi robot task allocation using genetic algorithms. Initially explored a simple GA written in Python and DEAP library that optimises for distance and time seperately using fitness functions F1 and F2. Then explored results to justify and develop naive multiobjective function F3 that optimises both goals. Eventually, we developed a more complex solution utilising NSGA-II algorithm.
UPDATES:
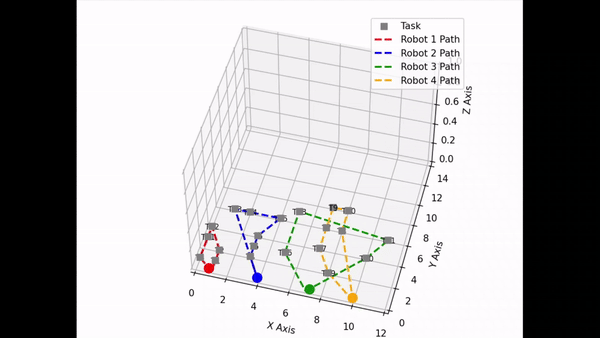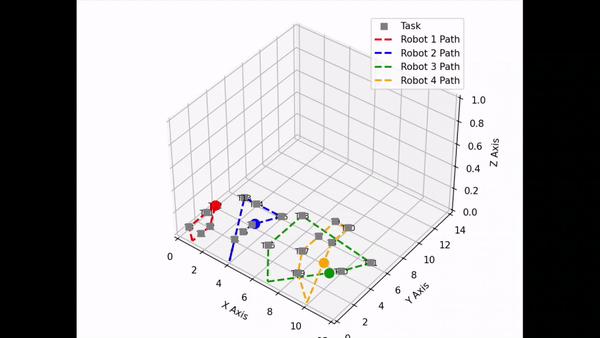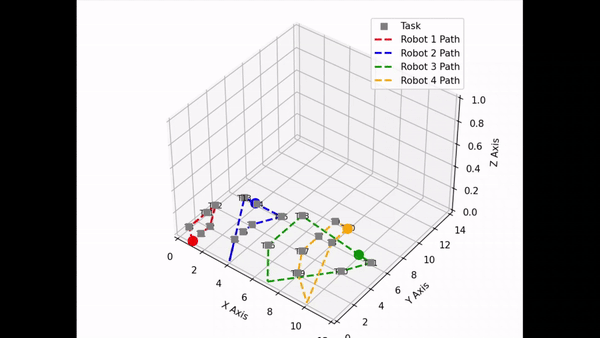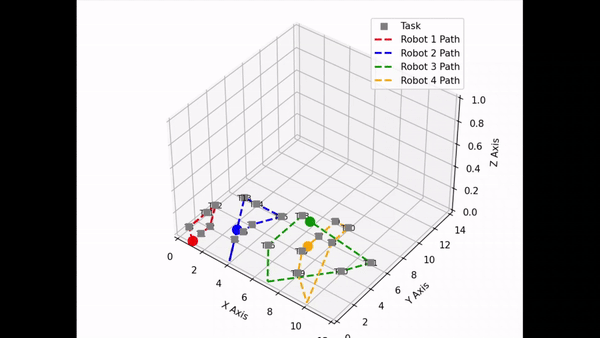
- Implemented 3D simulation over the original 2D view with animated visuals of robotic paths using Malplotlib Axes3C and FuncAnimation tools:
Then after comparing F1 and F2 solutions I found that their results varied significantly in failing to optimising for vice versa. Forexample when optimising for just distance not all the robots are allocated tasks to preserve battery but then we are not solving tasks concurrently and thus taking longer.
Simiarly, when solving for only time robots are exploring too far in order to ge tthe job done as quick as possible but pays no regard for preserving battery/distance.
After statistical analysis concluded that a significant conflict exists when optimising for time and distance.
Led to the development of a simple weighted fitness function F3 that equally optimised for both time and distance. I successfully obtained statistically significant and better solutions that optimised for both time and distance that outperformed F1 and F2.
While, this led to more balanced solutions although the diversity of the solutions were lacking as not all of these solutions were equally good.
Hence to improve and push my solutions further I developed a pure multiobjective solution utilising NSGA II algorithm. This was done to obtain a pareto front of solutions that were equally good.
The NSGA 2 solution obtained task allocations that generally performed much better than F3 as most of its solutions minimised time and distance much more that F3 solutions. Still there is room for improvement as one or two F3 solutions were similar to NSGA II solutions which could also be limitations of my environment.
Additionally, the hyperparameters for F3 were optimised as part of the experiments:
Further work includes adding more tasks and robots and positional variations. Current work is static task allocation and work can be done to provide a more dynamic scenario by implementing simulations in MATLAB / Webots.